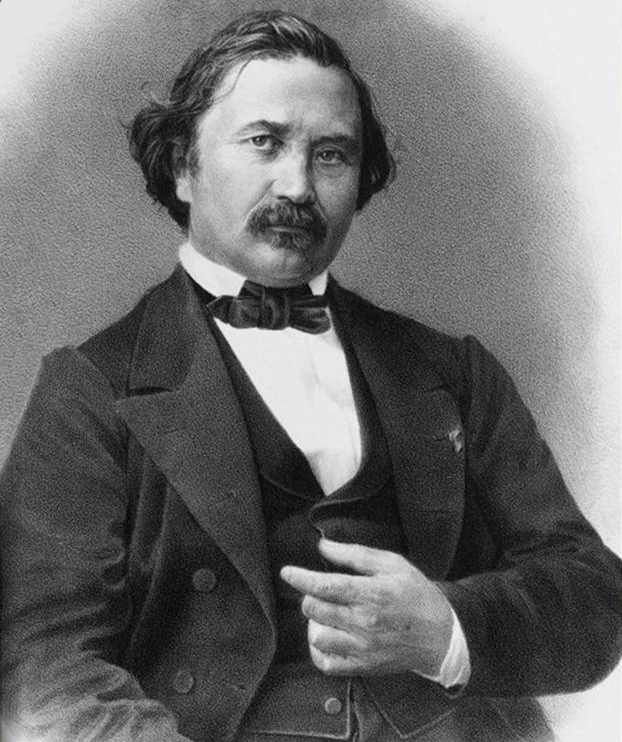|
Chebyshev Nets
Pafnuty Lvovich Chebyshev ( rus, Пафну́тий Льво́вич Чебышёв, p=pɐfˈnutʲɪj ˈlʲvovʲɪtɕ tɕɪbɨˈʂof) ( – ) was a Russian mathematician and considered to be the founding father of Russian mathematics. Chebyshev is known for his fundamental contributions to the fields of probability, statistics, mechanics, and number theory. A number of important mathematical concepts are named after him, including the Chebyshev inequality (which can be used to prove the weak law of large numbers), the Bertrand–Chebyshev theorem, Chebyshev polynomials, Chebyshev linkage, and Chebyshev bias. Transcription The surname Chebyshev has been transliterated in several different ways, like Tchebichef, Tchebychev, Tchebycheff, Tschebyschev, Tschebyschef, Tschebyscheff, Čebyčev, Čebyšev, Chebysheff, Chebychov, Chebyshov (according to native Russian speakers, this one provides the closest pronunciation in English to the correct pronunciation in old Russian), an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zhukovsky District, Kaluga Oblast
Zhukovsky District () is an administrativeCharter of Kaluga Oblast and municipalLaw #7-OZ district (raion), one of the twenty-four in Kaluga Oblast, Russia. It is located in the northeast of the oblast. The area of the district is . Its administrative center is the town A town is a type of a human settlement, generally larger than a village but smaller than a city. The criteria for distinguishing a town vary globally, often depending on factors such as population size, economic character, administrative stat ... of Zhukov. Population: 46,180 ( 2002 Census); The population of Zhukov accounts for 26.0% of the district's total population. References Notes Sources * * {{Use mdy dates, date=February 2013 Districts of Kaluga Oblast ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Number Theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions. Number theorists study prime numbers as well as the properties of mathematical objects constructed from integers (for example, rational numbers), or defined as generalizations of the integers (for example, algebraic integers). Integers can be considered either in themselves or as solutions to equations (Diophantine geometry). Questions in number theory can often be understood through the study of Complex analysis, analytical objects, such as the Riemann zeta function, that encode properties of the integers, primes or other number-theoretic objects in some fashion (analytic number theory). One may also study real numbers in relation to rational numbers, as for instance how irrational numbers can be approximated by fractions (Diophantine approximation). Number theory is one of the oldest branches of mathematics alongside geometry. One quirk of number theory is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
American Mathematical Society
The American Mathematical Society (AMS) is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, and serves the national and international community through its publications, meetings, advocacy and other programs. The society is one of the four parts of the Joint Policy Board for Mathematics and a member of the Conference Board of the Mathematical Sciences. History The AMS was founded in 1888 as the New York Mathematical Society, the brainchild of Thomas Fiske, who was impressed by the London Mathematical Society on a visit to England. John Howard Van Amringe became the first president while Fiske became secretary. The society soon decided to publish a journal, but ran into some resistance over concerns about competing with the '' American Journal of Mathematics''. The result was the ''Bulletin of the American Mathematical Society'', with Fiske as editor-in-chief. The de facto journal, as intended, was influentia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ISO 9
ISO 9 is an international standard establishing a system for the transliteration into Latin characters of Cyrillic characters constituting the alphabets of many Slavic and non-Slavic languages. Published on February 23, 1995 by the International Organization for Standardization, the major advantage ISO 9 has over other competing systems is its univocal system of one character for one character equivalents (by the use of diacritics), which faithfully represents the original spelling and allows for reverse transliteration, even if the language is unknown. Earlier versions of the standard, ISO/R 9:1954, ISO/R 9:1968 and ISO 9:1986, were more closely based on the international scholarly system for linguistics ( scientific transliteration), but have diverged in favour of unambiguous transliteration over phonemic representation. The edition of 1995 supersedes the edition of 1986. ISO 9:1995 The standard features three mapping tables: the first covers contemporary Slavic languages, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transliteration
Transliteration is a type of conversion of a text from one script to another that involves swapping letters (thus '' trans-'' + '' liter-'') in predictable ways, such as Greek → and → the digraph , Cyrillic → , Armenian → or Latin → . For instance, for the Greek term , which is usually translated as 'Hellenic Republic', the usual transliteration into the Latin script (romanization) is ; and the Russian term , which is usually translated as 'Russian Republic', can be transliterated either as or alternatively as . Transliteration is the process of representing or intending to represent a word, phrase, or text in a different script or writing system. Transliterations are designed to convey the pronunciation of the original word in a different script, allowing readers or speakers of that script to approximate the sounds and pronunciation of the original word. Transliterations do not change the pronunciation of the word. Thus, in the Greek above example, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Romanization Of Russian
The romanization of the Russian language (the transliteration of Russian text from the Cyrillic script into the Latin script), aside from its primary use for including Russian names and words in text written in a Latin alphabet, is also essential for computer users to input Russian text who either do not have a keyboard or word processor set up for inputting Cyrillic, or else are not capable of typing rapidly using a native Russian keyboard layout ( JCUKEN). In the latter case, they would type using a system of transliteration fitted for their keyboard layout, such as for English QWERTY keyboards, and then use an automated tool to convert the text into Cyrillic. Systematic transliterations of Cyrillic to Latin There are a number of distinct and competing standards for the romanization of Russian Cyrillic, with none of them having received much popularity, and, in reality, transliteration is often carried out without any consistent standards. Scientific transliteration Scien ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chebyshev Bias
In number theory, Chebyshev's bias is the phenomenon that most of the time, there are more primes of the form 4''k'' + 3 than of the form 4''k'' + 1, up to the same limit. This phenomenon was first observed by Russian mathematician Pafnuty Chebyshev in 1853. Description Let (''x''; ''n'', ''m'') denote the number of primes of the form ''nk'' + ''m'' up to ''x''. By the prime number theorem (extended to arithmetic progression), :\pi(x;4,1)\sim\pi(x;4,3)\sim \frac\frac. That is, half of the primes are of the form 4''k'' + 1, and half of the form 4''k'' + 3. A reasonable guess would be that (''x''; 4, 1) > (''x''; 4, 3) and (''x''; 4, 1) < (''x''; 4, 3) each also occur 50% of the time. This, however, is not supported by numerical evidence — in fact, (''x''; 4, 3) > (''x''; 4, 1) occurs much more frequently. For example, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chebyshev Linkage
In kinematics, Chebyshev's linkage is a four-bar linkage that converts rotational motion to approximate linear motion. It was invented by the 19th-century mathematician Pafnuty Chebyshev, who studied theoretical problems in kinematic Mechanism (engineering), mechanisms. One of the problems was the construction of a linkage that converts a rotary motion into an approximate straight-line motion (a straight line mechanism). This was also studied by James Watt in his improvements to the steam engine, which resulted in Watt's linkage. – Cross link straight-line mechanism Equations of motion The motion of the linkage can be constrained to an input angle that may be changed through velocities, forces, etc. The input angles can be either link ''L''2 with the horizontal or link ''L ...[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chebyshev Polynomial
The Chebyshev polynomials are two sequences of orthogonal polynomials related to the trigonometric functions, cosine and sine functions, notated as T_n(x) and U_n(x). They can be defined in several equivalent ways, one of which starts with trigonometric functions: The Chebyshev polynomials of the first kind T_n are defined by T_n(\cos \theta) = \cos(n\theta). Similarly, the Chebyshev polynomials of the second kind U_n are defined by U_n(\cos \theta) \sin \theta = \sin\big((n + 1)\theta\big). That these expressions define polynomials in \cos\theta is not obvious at first sight but can be shown using de Moivre's formula (see #Trigonometric definition, below). The Chebyshev polynomials are polynomials with the largest possible leading coefficient whose absolute value on the interval (mathematics), interval is bounded by 1. They are also the "extremal" polynomials for many other properties. In 1952, Cornelius Lanczos showed that the Chebyshev polynomials are important in a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bertrand's Postulate
In number theory, Bertrand's postulate is the theorem that for any integer n > 3, there exists at least one prime number p with :n < p < 2n - 2. A less restrictive formulation is: for every , there is always at least one prime such that : Another formulation, where is the -th prime, is: for : This statement was first conjectured in 1845 by Joseph Bertrand (1822–1900). Bertrand himself verified his statement for all integers . His conjecture was completely Proof of Bertrand's postulate, proved by Pafnuty Chebyshev, Chebyshev (1821–1894) in 1852 and so the postulate is also called the Bertrand–Chebyshev theorem or Chebyshev's theorem. Chebyshev's theorem can also be stated as a relationship with , the prime-counting function (number of primes less than or equal to ): ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weak Law Of Large Numbers
In probability theory, the law of large numbers is a mathematical law that states that the average of the results obtained from a large number of independent random samples converges to the true value, if it exists. More formally, the law of large numbers states that given a sample of independent and identically distributed values, the sample mean converges to the true mean. The law of large numbers is important because it guarantees stable long-term results for the averages of some random events. For example, while a casino may lose money in a single spin of the roulette wheel, its earnings will tend towards a predictable percentage over a large number of spins. Any winning streak by a player will eventually be overcome by the parameters of the game. Importantly, the law applies (as the name indicates) only when a ''large number'' of observations are considered. There is no principle that a small number of observations will coincide with the expected value or that a strea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chebyshev Inequality
In probability theory, Chebyshev's inequality (also called the Bienaymé–Chebyshev inequality) provides an upper bound on the probability of deviation of a random variable (with finite variance) from its mean. More specifically, the probability that a random variable deviates from its mean by more than k\sigma is at most 1/k^2, where k is any positive constant and \sigma is the standard deviation (the square root of the variance). The rule is often called Chebyshev's theorem, about the range of standard deviations around the mean, in statistics. The inequality has great utility because it can be applied to any probability distribution in which the mean and variance are defined. For example, it can be used to prove the weak law of large numbers. Its practical usage is similar to the 68–95–99.7 rule, which applies only to normal distributions. Chebyshev's inequality is more general, stating that a minimum of just 75% of values must lie within two standard deviations of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |