|
Celestial Coordinates
In astronomy, coordinate systems are used for specifying positions of celestial objects (satellites, planets, stars, galaxies, etc.) relative to a given reference frame, based on physical reference points available to a situated observer (e.g. the true horizon and north to an observer on Earth's surface). Coordinate systems in astronomy can specify an object's relative position in three-dimensional space or plot merely by its direction on a celestial sphere, if the object's distance is unknown or trivial. Spherical coordinates, projected on the celestial sphere, are analogous to the geographic coordinate system used on the surface of Earth. These differ in their choice of fundamental plane, which divides the celestial sphere into two equal hemispheres along a great circle. Rectangular coordinates, in appropriate units, have the same fundamental () plane and primary (-axis) direction, such as an axis of rotation. Each coordinate system is named after its choice of funda ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equatorial Coordinate System
The equatorial coordinate system is a celestial coordinate system widely used to specify the positions of astronomical object, celestial objects. It may be implemented in spherical coordinate system, spherical or Cartesian coordinate system, rectangular coordinates, both defined by an origin (mathematics), origin at the centre of Earth, a fundamental plane (spherical coordinates), fundamental plane consisting of the projective geometry, projection of Earth's equator onto the celestial sphere (forming the celestial equator), a primary direction towards the March equinox, March equinox (celestial coordinates), equinox, and a right-hand rule, right-handed convention. The origin at the centre of Earth means the coordinates are ''geocentric model, geocentric'', that is, as seen from the centre of Earth as if it were transparency and translucency, transparent. The fundamental plane and the primary direction mean that the coordinate system, while aligned with Earth's equator and geograp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Primary Direction
The equatorial coordinate system is a celestial coordinate system widely used to specify the positions of celestial objects. It may be implemented in spherical or rectangular coordinates, both defined by an origin at the centre of Earth, a fundamental plane consisting of the projection of Earth's equator onto the celestial sphere (forming the celestial equator), a primary direction towards the March equinox, and a right-handed convention. The origin at the centre of Earth means the coordinates are '' geocentric'', that is, as seen from the centre of Earth as if it were transparent. The fundamental plane and the primary direction mean that the coordinate system, while aligned with Earth's equator and pole, does not rotate with the Earth, but remains relatively fixed against the background stars. A right-handed convention means that coordinates increase northward from and eastward around the fundamental plane. Primary direction This description of the orientation of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
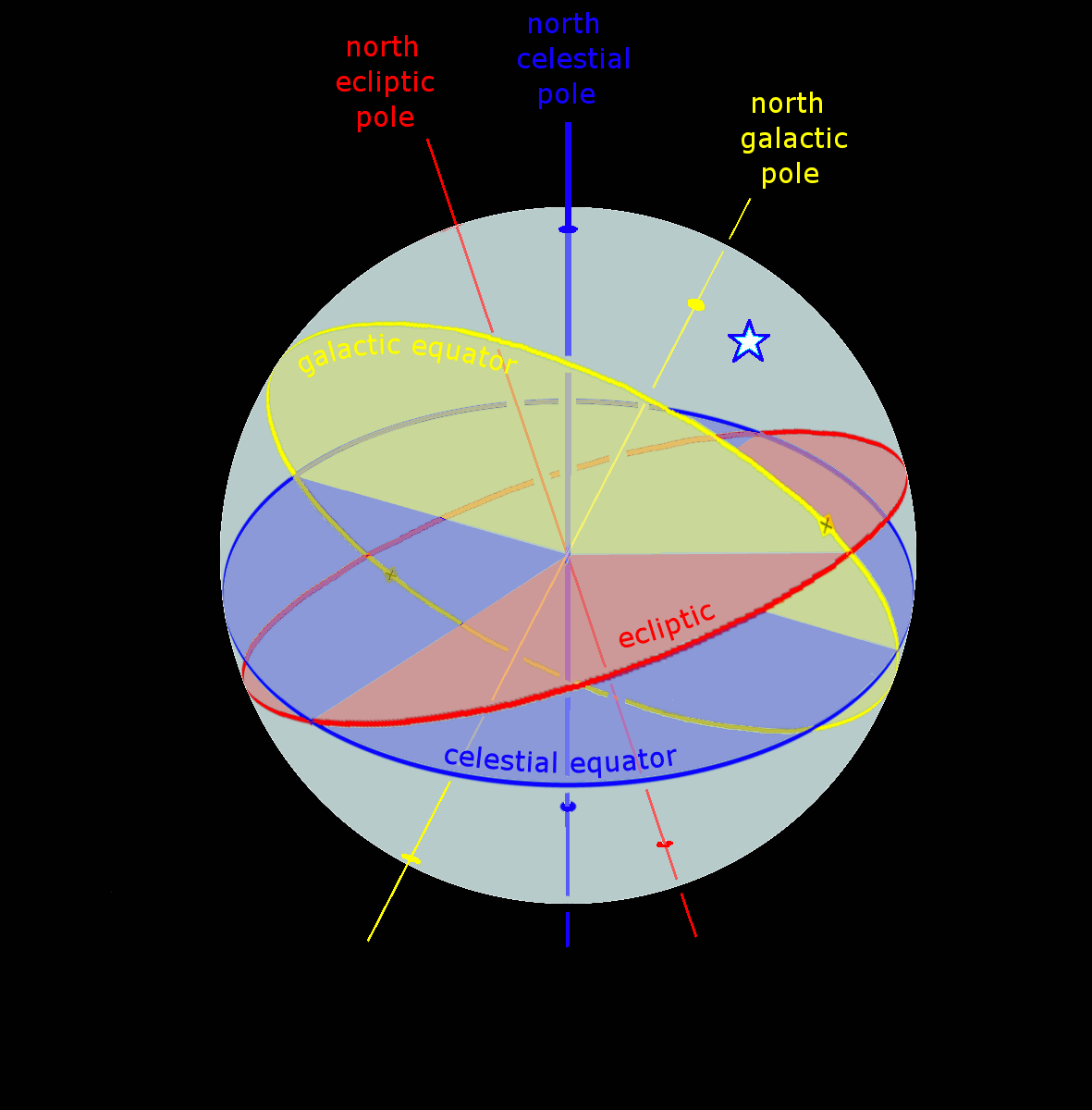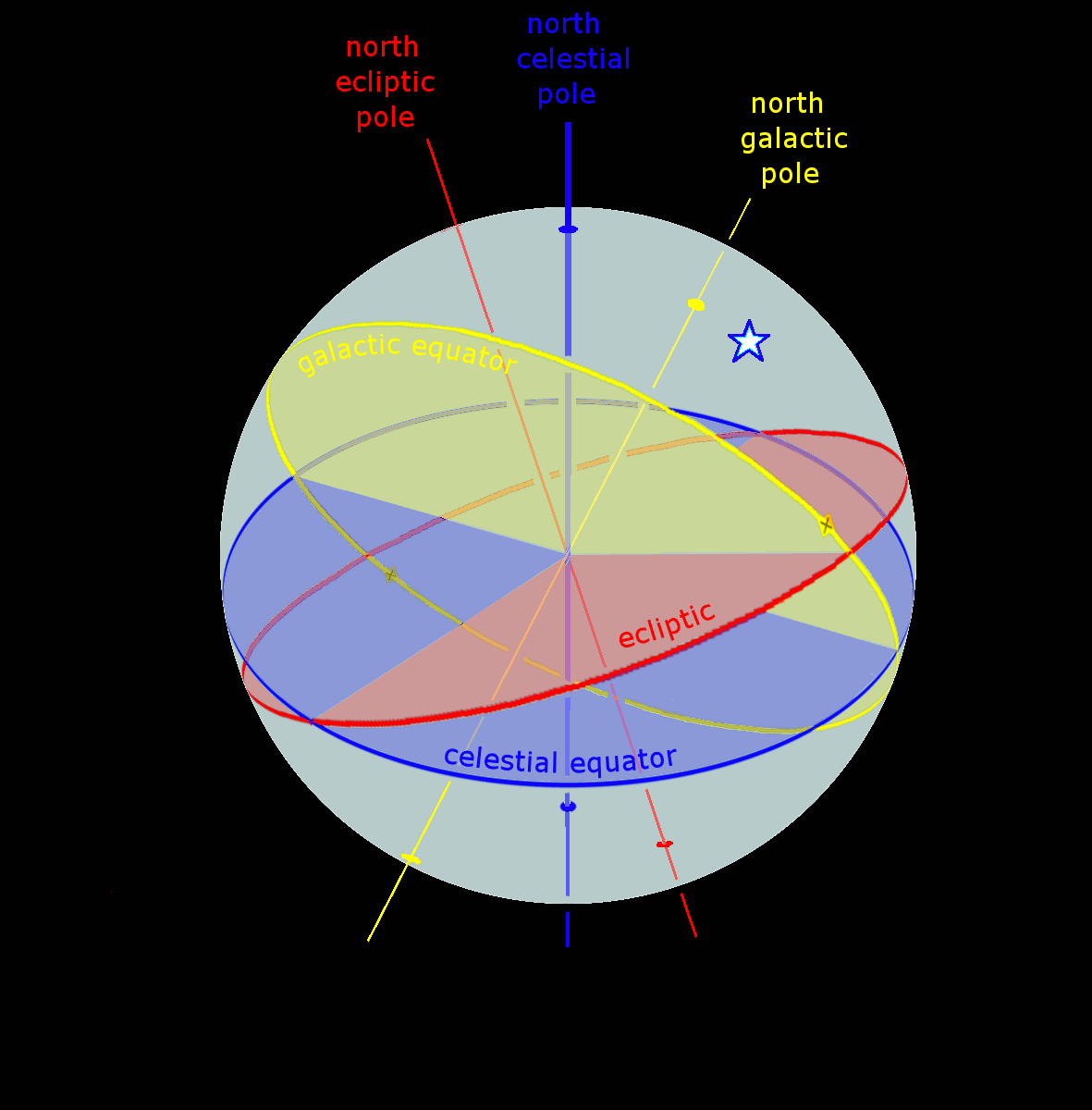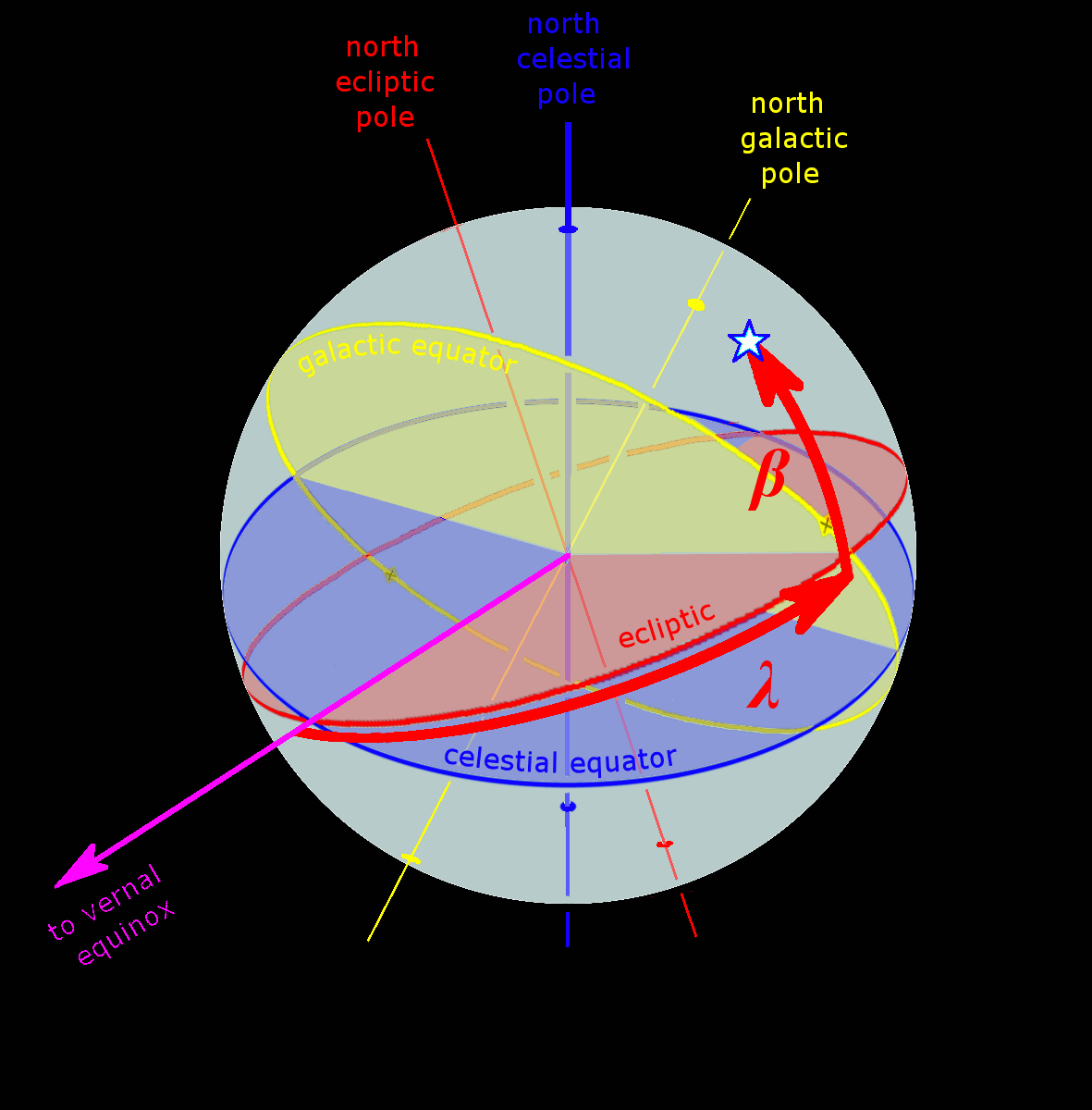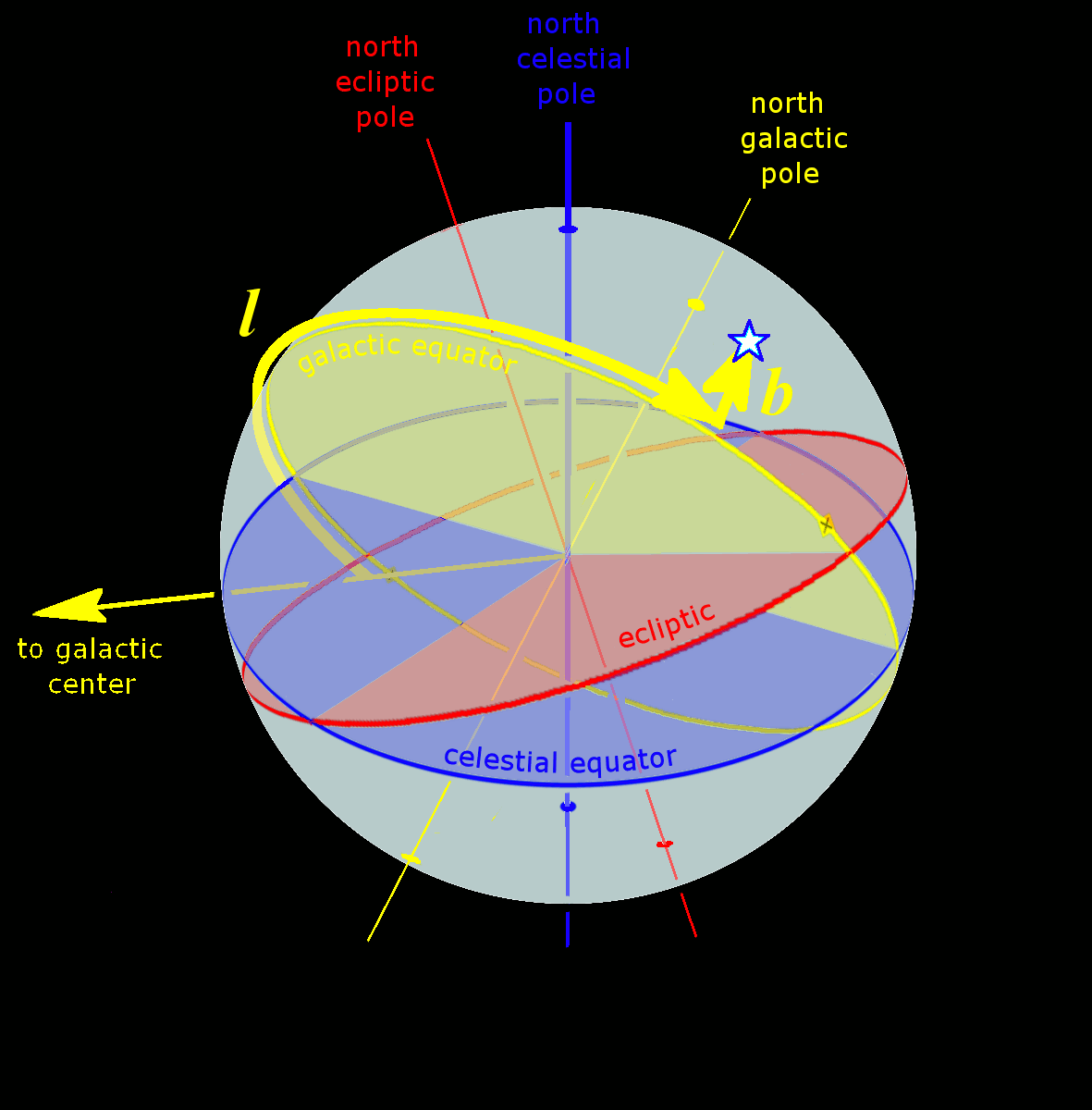
Ecliptic Equator Galactic Anim
The ecliptic or ecliptic plane is the orbital plane of Earth's orbit, Earth around the Sun. It was a central concept in a number of ancient sciences, providing the framework for key measurements in astronomy, astrology and calendar-making. From the perspective of an observer on Earth, the Sun's movement around the celestial sphere over the course of a year traces out a path along the ecliptic against the fixed stars, background of stars – specifically the Zodiac constellations. The planets of the Solar System can also be seen along the ecliptic, because their orbital planes are very close to Earth's. The Moon's orbital plane is also similar to Earth's; the ecliptic is so named because the ancients noted that eclipses only occur when the Moon is crossing it. The ecliptic is an important Plane of reference, reference plane and is the basis of the ecliptic coordinate system. Ancient scientists were able to calculate Earth's axial tilt by comparing the ecliptic plane to that of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
American Astronomical Society
The American Astronomical Society (AAS, sometimes spoken as "double-A-S") is an American society of professional astronomers and other interested individuals, headquartered in Washington, DC. The primary objective of the AAS is to promote the advancement of astronomy and closely related branches of science, while the secondary purpose includes enhancing astronomy education and providing a political voice for its members through lobbying and grassroots activities. Its current mission is to enhance and share humanity's scientific understanding of the universe as a diverse and inclusive astronomical community. History The society was founded in 1899 through the efforts of George Ellery Hale. The constitution of the group was written by Hale, George Comstock, Edward Morley, Simon Newcomb and Edward Charles Pickering. These men, plus four others, were the first Executive Council of the society; Newcomb was the first president. The initial membership was 114. The AAS name of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rotation Around A Fixed Axis
Rotation around a fixed axis or axial rotation is a special case of rotational motion around an ''axis of rotation'' fixed, stationary, or static in three-dimensional space. This type of motion excludes the possibility of the instantaneous axis of rotation changing its orientation (geometry), orientation and cannot describe such phenomena as nutation, wobbling or precession. According to Euler's rotation theorem, simultaneous rotation along a number of stationary axes at the same time is impossible; if two rotations are forced at the same time, a new axis of rotation will result. This concept assumes that the rotation is also stable, such that no torque is required to keep it going. The kinematics and dynamics (mechanics), dynamics of rotation around a fixed axis of a rigid body are mathematically much simpler than those for Rigid body dynamics#Rigid-body angular momentum, free rotation of a rigid body; they are entirely analogous to those of linear motion along a single fixed di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Units Of Measurement
A unit of measurement, or unit of measure, is a definite magnitude (mathematics), magnitude of a quantity, defined and adopted by convention or by law, that is used as a standard for measurement of the same kind of quantity. Any other quantity of that kind can be expressed as a multiple of the unit of measurement. For example, a length is a physical quantity. The metre (symbol m) is a unit of length that represents a definite predetermined length. For instance, when referencing "10 metres" (or 10 m), what is actually meant is 10 times the definite predetermined length called "metre". The definition, agreement, and practical use of units of measurement have played a crucial role in human endeavour from early ages up to the present. A multitude of System of measurement, systems of units used to be very common. Now there is a global standard, the International System of Units (SI), the modern form of the metric system. In trade, weights and measures are often a su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartesian Coordinate System
In geometry, a Cartesian coordinate system (, ) in a plane (geometry), plane is a coordinate system that specifies each point (geometry), point uniquely by a pair of real numbers called ''coordinates'', which are the positive and negative numbers, signed distances to the point from two fixed perpendicular oriented lines, called ''coordinate lines'', ''coordinate axes'' or just ''axes'' (plural of ''axis'') of the system. The point where the axes meet is called the ''Origin (mathematics), origin'' and has as coordinates. The axes direction (geometry), directions represent an orthogonal basis. The combination of origin and basis forms a coordinate frame called the Cartesian frame. Similarly, the position of any point in three-dimensional space can be specified by three ''Cartesian coordinates'', which are the signed distances from the point to three mutually perpendicular planes. More generally, Cartesian coordinates specify the point in an -dimensional Euclidean space for any di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great Circle
In mathematics, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere's center point. Discussion Any arc of a great circle is a geodesic of the sphere, so that great circles in spherical geometry are the natural analog of straight lines in Euclidean space. For any pair of distinct non- antipodal points on the sphere, there is a unique great circle passing through both. (Every great circle through any point also passes through its antipodal point, so there are infinitely many great circles through two antipodal points.) The shorter of the two great-circle arcs between two distinct points on the sphere is called the ''minor arc'', and is the shortest surface-path between them. Its arc length is the great-circle distance between the points (the intrinsic distance on a sphere), and is proportional to the measure of the central angle formed by the two points and the center of the sphere. A great circle is the largest ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sphere
A sphere (from Ancient Greek, Greek , ) is a surface (mathematics), surface analogous to the circle, a curve. In solid geometry, a sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the center (geometry), ''center'' of the sphere, and the distance is the sphere's ''radius''. The earliest known mentions of spheres appear in the work of the Greek mathematics, ancient Greek mathematicians. The sphere is a fundamental surface in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubble (physics), Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is spherical Earth, often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres rolling, roll smoothly in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamental Plane (spherical Coordinates)
The fundamental plane in a spherical coordinate system is a plane of reference that divides the sphere into two hemispheres. The geocentric latitude of a point is then the angle between the fundamental plane and the line joining the point to the centre of the sphere. For a geographic coordinate system of the Earth, the fundamental plane is the Equator. Astronomical coordinate systems have varying fundamental planes: * The horizontal coordinate system uses the observer's horizon. * The Besselian coordinate system uses Earth's terminator (day/night boundary). This is a Cartesian coordinate system (''x'', ''y'', ''z''). * The equatorial coordinate system uses the celestial equator. * The ecliptic coordinate system uses the ecliptic. * The galactic coordinate system uses the Milky Way The Milky Way or Milky Way Galaxy is the galaxy that includes the Solar System, with the name describing the #Appearance, galaxy's appearance from Earth: a hazy band of light seen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Earth
Earth is the third planet from the Sun and the only astronomical object known to Planetary habitability, harbor life. This is enabled by Earth being an ocean world, the only one in the Solar System sustaining liquid surface water. Almost all of Earth's water is contained in its global ocean, covering Water distribution on Earth, 70.8% of Earth's crust. The remaining 29.2% of Earth's crust is land, most of which is located in the form of continental landmasses within Earth's land hemisphere. Most of Earth's land is at least somewhat humid and covered by vegetation, while large Ice sheet, sheets of ice at Polar regions of Earth, Earth's polar polar desert, deserts retain more water than Earth's groundwater, lakes, rivers, and Water vapor#In Earth's atmosphere, atmospheric water combined. Earth's crust consists of slowly moving tectonic plates, which interact to produce mountain ranges, volcanoes, and earthquakes. Earth's outer core, Earth has a liquid outer core that generates a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geographic Coordinate System
A geographic coordinate system (GCS) is a spherical coordinate system, spherical or geodetic coordinates, geodetic coordinate system for measuring and communicating position (geometry), positions directly on Earth as latitude and longitude. It is the simplest, oldest, and most widely used type of the various spatial reference systems that are in use, and forms the basis for most others. Although latitude and longitude form a coordinate tuple like a cartesian coordinate system, the geographic coordinate system is not cartesian because the measurements are angles and are not on a planar surface. A full GCS specification, such as those listed in the EPSG Geodetic Parameter Dataset, EPSG and ISO 19111 standards, also includes a choice of geodetic datum (including an Earth ellipsoid), as different datums will yield different latitude and longitude values for the same location. History The invention of a geographic coordinate system is generally credited to Eratosthenes of Cy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |