|
Catenoid
In geometry, a catenoid is a type of surface, arising by rotating a catenary curve about an axis (a surface of revolution). It is a minimal surface, meaning that it occupies the least area when bounded by a closed space. It was formally described in 1744 by the mathematician Leonhard Euler. Soap film attached to twin circular rings will take the shape of a catenoid. Because they are members of the same associate family of surfaces, a catenoid can be bent into a portion of a helicoid, and vice versa. Geometry The catenoid was the first non-trivial minimal surface in 3-dimensional Euclidean space to be discovered apart from the plane. The catenoid is obtained by rotating a catenary about its directrix. It was found and proved to be minimal by Leonhard Euler Leonhard Euler ( ; ; ; 15 April 170718 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Helicoid
The helicoid, also known as helical surface, is a smooth Surface (differential geometry), surface embedded in three-dimensional space. It is the surface traced by an infinite line that is simultaneously being rotated and lifted along its Rotation around a fixed axis, fixed axis of rotation. It is the third minimal surface to be known, after the Plane (geometry), plane and the catenoid. Description It was described by Euler in 1774 and by Jean Baptiste Meusnier in 1776. Its Nomenclature, name derives from its similarity to the helix: for every Point (geometry), point on the helicoid, there is a helix contained in the helicoid which passes through that point. The helicoid is also a ruled surface (and a right conoid), meaning that it is a trace of a line. Alternatively, for any point on the surface, there is a line on the surface passing through it. Indeed, Eugène Charles Catalan, Catalan proved in 1842 that the helicoid and the plane were the only ruled minimal surfaces. A helic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minimal Surfaces Of Revolution
In mathematics, a minimal surface of revolution or minimum surface of revolution is a surface of revolution defined from two points in a half-plane, whose boundary is the axis of revolution of the surface. It is generated by a curve that lies in the half-plane and connects the two points; among all the surfaces that can be generated in this way, it is the one that minimizes the surface area. A basic problem in the calculus of variations is finding the curve between two points that produces this minimal surface of revolution. Relation to minimal surfaces A minimal surface of revolution is a subtype of minimal surface. A minimal surface is defined not as a surface of minimal area, but as a surface with a mean curvature of 0. Since a mean curvature of 0 is a necessary condition of a surface of minimal area, all minimal surfaces of revolution are minimal surfaces, but not all minimal surfaces are minimal surfaces of revolution. As a point forms a circle when rotated about an axis, fin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Catenary
In physics and geometry, a catenary ( , ) is the curve that an idealized hanging chain or wire rope, cable assumes under its own weight when supported only at its ends in a uniform gravitational field. The catenary curve has a U-like shape, superficially similar in appearance to a parabola, which it is not. The curve appears in the design of certain types of Catenary arch, arches and as a cross section of the catenoid—the shape assumed by a soap film bounded by two parallel circular rings. The catenary is also called the alysoid, chainette,#MathWorld, MathWorld or, particularly in the materials sciences, an example of a funicular curve, funicular. Rope statics describes catenaries in a classic statics problem involving a hanging rope. Mathematically, the catenary curve is the Graph of a function, graph of the hyperbolic cosine function. The surface of revolution of the catenary curve, the catenoid, is a minimal surface, specifically a minimal surface of revolution. A ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Associate Family
In differential geometry, the associate family (or Bonnet family) of a minimal surface is a one-parameter family of minimal surfaces which share the same Weierstrass data. That is, if the surface has the representation :x_k(\zeta) = \Re \left\ + c_k , \qquad k=1,2,3 the family is described by :x_k(\zeta,\theta) = \Re \left\ + c_k , \qquad \theta \in ,2\pi where \Re indicates the real part of a complex number. For ''θ'' = ''π''/2 the surface is called the conjugate of the ''θ'' = 0 surface. The transformation can be viewed as locally rotating the principal curvature In differential geometry, the two principal curvatures at a given point of a surface (mathematics), surface are the maximum and minimum values of the curvature as expressed by the eigenvalues of the shape operator at that point. They measure how ... directions. The surface normals of a point with a fixed ''ζ'' remains unchanged as ''θ'' changes; the point itself moves along an ellipse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minimal Surface
In mathematics, a minimal surface is a surface that locally minimizes its area. This is equivalent to having zero mean curvature (see definitions below). The term "minimal surface" is used because these surfaces originally arose as surfaces that minimized total surface area subject to some constraint. Physical models of area-minimizing minimal surfaces can be made by dipping a wire frame into a soap solution, forming a soap film, which is a minimal surface whose boundary is the wire frame. However, the term is used for more general surfaces that may self-intersect or do not have constraints. For a given constraint there may also exist several minimal surfaces with different areas (for example, see minimal surface of revolution): the standard definitions only relate to a local optimum, not a global optimum. Definitions Minimal surfaces can be defined in several equivalent ways in \R^3. The fact that they are equivalent serves to demonstrate how minimal surface theory lies at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
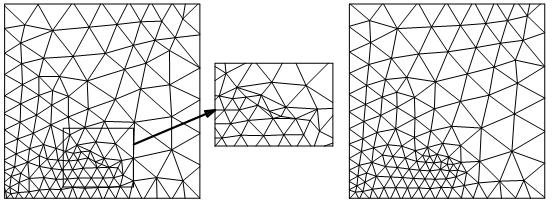
Stretched Grid Method
The stretched grid method (SGM) is a Numerical analysis, numerical technique for finding approximate solutions of various mathematical and engineering problems that can be related to an elastic grid behavior. In particular, meteorologists use the stretched grid method for weather prediction and engineers use the stretched grid method to design tents and other tensile structures. FEM and BEM mesh refinement In recent decades the finite element method, finite element and boundary element methods (FEM and BEM) have become a mainstay for industrial engineering design and analysis. Increasingly larger and more complex designs are being simulated using the FEM or BEM. However, some problems of FEM and BEM engineering analysis are still on the cutting edge. The first problem is a reliability of engineering analysis that strongly depends upon the quality of initial data generated at the pre-processing stage. It is known that automatic element mesh generation techniques at this stage have ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minimal Surfaces
In mathematics, a minimal surface is a surface that locally minimizes its area. This is equivalent to having zero mean curvature (see definitions below). The term "minimal surface" is used because these surfaces originally arose as surfaces that minimized total surface area subject to some constraint. Physical models of area-minimizing minimal surfaces can be made by dipping a wire frame into a soap solution, forming a soap film, which is a minimal surface whose boundary is the wire frame. However, the term is used for more general surfaces that may Immersed submanifold#Immersed submanifolds, self-intersect or do not have constraints. For a given constraint there may also exist several minimal surfaces with different areas (for example, see minimal surface of revolution): the standard definitions only relate to a local optimum, not a global optimum. Definitions Minimal surfaces can be defined in several equivalent ways in \R^3. The fact that they are equivalent serves to demons ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Of Revolution
A surface of revolution is a Surface (mathematics), surface in Euclidean space created by rotating a curve (the ''generatrix'') one full revolution (unit), revolution around an ''axis of rotation'' (normally not Intersection (geometry), intersecting the generatrix, except at its endpoints). The volume bounded by the surface created by this revolution is the ''solid of revolution''. Examples of surfaces of revolution generated by a straight line are cylinder (geometry), cylindrical and conical surfaces depending on whether or not the line is parallel to the axis. A circle that is rotated around any diameter generates a sphere of which it is then a great circle, and if the circle is rotated around an axis that does not intersect the interior of a circle, then it generates a torus which does not intersect itself (a ring torus). Properties The sections of the surface of revolution made by planes through the axis are called ''meridional sections''. Any meridional section can be consi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Curvature
In mathematics, the mean curvature H of a surface S is an ''extrinsic'' measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space. The concept was used by Sophie Germain in her work on elasticity theory. Jean Baptiste Marie Meusnier used it in 1776, in his studies of minimal surfaces. It is important in the analysis of minimal surfaces, which have mean curvature zero, and in the analysis of physical interfaces between fluids (such as soap films) which, for example, have constant mean curvature in static flows, by the Young–Laplace equation. Definition Let p be a point on the surface S inside the three dimensional Euclidean space . Each plane through p containing the normal line to S cuts S in a (plane) curve. Fixing a choice of unit normal gives a signed curvature to that curve. As the plane is rotated by an angle \theta (always containing the normal line) that cur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surfaces Of Revolution
A surface of revolution is a surface in Euclidean space created by rotating a curve (the '' generatrix'') one full revolution around an ''axis of rotation'' (normally not intersecting the generatrix, except at its endpoints). The volume bounded by the surface created by this revolution is the ''solid of revolution''. Examples of surfaces of revolution generated by a straight line are cylindrical and conical surfaces depending on whether or not the line is parallel to the axis. A circle that is rotated around any diameter generates a sphere of which it is then a great circle, and if the circle is rotated around an axis that does not intersect the interior of a circle, then it generates a torus which does not intersect itself (a ring torus). Properties The sections of the surface of revolution made by planes through the axis are called ''meridional sections''. Any meridional section can be considered to be the generatrix in the plane determined by it and the axis. The sections ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |