|
CUSUM
In statistical process control, statistical quality control, the CUSUM (or cumulative sum control chart) is a sequential analysis technique developed by E. S. Page of the University of Cambridge. It is typically used for monitoring change detection. CUSUM was announced in Biometrika, in 1954, a few years after the publication of Abraham Wald, Wald's sequential probability ratio test (SPRT). E. S. Page referred to a "quality number" \theta, by which he meant a parameter of the probability distribution; for example, the mean. He devised CUSUM as a method to determine changes in it, and proposed a criterion for deciding when to take corrective action. When the CUSUM method is applied to changes in mean, it can be used for step detection of a time series. A few years later, George Alfred Barnard developed a visualization method, the V-mask chart, to detect both increases and decreases in \theta. Method As its name implies, CUSUM involves the calculation of a cumulative sum (which is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sequential Probability Ratio Test
The sequential probability ratio test (SPRT) is a specific Sequential analysis, sequential hypothesis test, developed by Abraham Wald and later proven to be optimal by Wald and Jacob Wolfowitz. Neyman–Pearson lemma, Neyman and Pearson's 1933 result inspired Wald to reformulate it as a sequential analysis problem. The Neyman-Pearson lemma, by contrast, offers a rule of thumb for when all the data is collected (and its likelihood ratio known). While originally developed for use in quality control studies in the realm of manufacturing, SPRT has been formulated for use in the computerized testing of human examinees as a termination criterion. Theory As in classical hypothesis testing, SPRT starts with a pair of hypotheses, say H_0 and H_1 for the null hypothesis and alternative hypothesis respectively. They must be specified as follows: :H_0: p=p_0 :H_1: p=p_1 The next step is to calculate the cumulative sum of the log-likelihood-ratio test, likelihood ratio, \log \Lambda_i, as ne ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sequential Analysis
In statistics, sequential analysis or sequential hypothesis testing is statistical analysis where the sample size is not fixed in advance. Instead data is evaluated as it is collected, and further sampling is stopped in accordance with a pre-defined stopping rule as soon as significant results are observed. Thus a conclusion may sometimes be reached at a much earlier stage than would be possible with more classical hypothesis testing or estimation, at consequently lower financial and/or human cost. History The method of sequential analysis is first attributed to Abraham Wald with Jacob Wolfowitz, W. Allen Wallis, and Milton Friedman while at Columbia University, Columbia University's Applied Mathematics Panel, Statistical Research Group as a tool for more efficient industrial quality control during World War II. Its value to the war effort was immediately recognised, and led to its receiving a "restricted" Classified information, classification. At the same time, George Alfre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Step Detection
In statistics and signal processing, step detection (also known as step smoothing, step filtering, shift detection, jump detection or edge detection) is the process of finding abrupt changes (steps, jumps, shifts) in the mean level of a time series or signal. It is usually considered as a special case of the statistical method known as change detection or change point detection. Often, the step is small and the time series is corrupted by some kind of noise, and this makes the problem challenging because the step may be hidden by the noise. Therefore, statistical and/or signal processing algorithms are often required. The step detection problem occurs in multiple scientific and engineering contexts, for example in statistical process control (the control chart being the most directly related method), in exploration geophysics (where the problem is to segment a well-log recording into stratigraphic zones), in genetics (the problem of separating microarray data into similar copy-n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time Series
In mathematics, a time series is a series of data points indexed (or listed or graphed) in time order. Most commonly, a time series is a sequence taken at successive equally spaced points in time. Thus it is a sequence of discrete-time data. Examples of time series are heights of ocean tides, counts of sunspots, and the daily closing value of the Dow Jones Industrial Average. A time series is very frequently plotted via a run chart (which is a temporal line chart). Time series are used in statistics, signal processing, pattern recognition, econometrics, mathematical finance, weather forecasting, earthquake prediction, electroencephalography, control engineering, astronomy, communications engineering, and largely in any domain of applied science and engineering which involves temporal measurements. Time series ''analysis'' comprises methods for analyzing time series data in order to extract meaningful statistics and other characteristics of the data. Time series ''f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variable And Attribute (research)
In science and research, an attribute is a quality of an object (person, thing, etc.). Earl R. Babbie, ''The Practice of Social Research'', 12th edition, Wadsworth Publishing, 2009, , p. 14-18 Attributes are closely related to variables. A variable is a logical set of attributes. Variables can "vary" – for example, be high or low. How high, or how low, is determined by the value of the attribute (and in fact, an attribute could be just the word "low" or "high"). ''(For example see: Binary option)'' While an attribute is often intuitive, the variable is the operationalized way in which the attribute is represented for further data processing. In data processing data are often represented by a combination of ''items'' (objects organized in rows), and multiple variables (organized in columns). Values of each variable statistically "vary" (or are distributed) across the variable's domain. A domain is a set of all possible values that a variable is allowed to have. The values are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Figure Of Merit
A figure of merit (FOM) is a performance metric that characterizes the performance of a device, system, or method, relative to its alternatives. Examples *Absolute alcohol content per currency unit in an alcoholic beverage *accurizing, Accuracy of a rifle *Audio amplifier figures of merit such as gain or efficiency *Battery life of a laptop computer New York Times, June 25, 2009 *Calories per serving *Clock rate of a CPU is often given as a figure of merit, but is of limited use in comparing between different architectures. FLOPS may be a better figure, though these too are not completely representative of the performance of a CPU. *Contrast ratio of an LCD *Frequency response of a Loudspeaker, speaker *Fill factor (solar cell), Fill factor of a solar cell *Image resolutio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Charts And Diagrams
Statistics (from German: ', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An experimental study involves taking measurements of the sy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
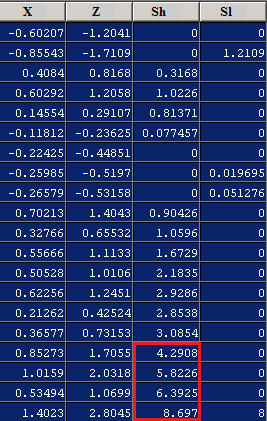
Example Cusum2
Example may refer to: * ''exempli gratia'' (e.g.), usually read out in English as "for example" * .example, reserved as a domain name that may not be installed as a top-level domain of the Internet ** example.com, example.net, example.org, and example.edu: second-level domain names reserved for use in documentation as examples * HMS ''Example'' (P165), an Archer-class patrol and training vessel of the Royal Navy Arts * ''The Example'', a 1634 play by James Shirley * ''The Example'' (comics), a 2009 graphic novel by Tom Taylor and Colin Wilson * Example (musician), the British dance musician Elliot John Gleave (born 1982) * ''Example'' (album), a 1995 album by American rock band For Squirrels See also * Exemplar (other), a prototype or model which others can use to understand a topic better * Exemplum, medieval collections of short stories to be told in sermons * Eixample The Eixample (, ) is a district of Barcelona between the old city (Ciutat Vella) a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Type II Error
Type I error, or a false positive, is the erroneous rejection of a true null hypothesis in statistical hypothesis testing. A type II error, or a false negative, is the erroneous failure in bringing about appropriate rejection of a false null hypothesis. Type I errors can be thought of as errors of commission, in which the status quo is erroneously rejected in favour of new, misleading information. Type II errors can be thought of as errors of omission, in which a misleading status quo is allowed to remain due to failures in identifying it as such. For example, if the assumption that people are ''innocent until proven guilty'' were taken as a null hypothesis, then proving an innocent person as guilty would constitute a Type I error, while failing to prove a guilty person as guilty would constitute a Type II error. If the null hypothesis were inverted, such that people were by default presumed to be ''guilty until proven innocent'', then proving a guilty person's innocence would ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Research Memoirs
Statistics (from German: ', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An experimental study involves taking measurements of the syst ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |