|
C-parity
In physics, the C parity or charge parity is a multiplicative quantum number of some particles that describes their behavior under the symmetry operation of charge conjugation. Charge conjugation changes the sign of all quantum charges (that is, additive quantum numbers), including the electrical charge, baryon number and lepton number, and the flavor charges strangeness, charm, bottomness, topness and Isospin (''I''3). In contrast, it doesn't affect the mass, linear momentum or spin of a particle. Formalism Consider an operation \mathcal that transforms a particle into its antiparticle, :\mathcal C \, , \psi\rangle = , \bar \rangle. Both states must be normalizable, so that : 1 = \langle \psi , \psi \rangle = \langle \bar , \bar \rangle = \langle \psi , \mathcal^\dagger \mathcal C, \psi \rangle, which implies that \mathcal C is unitary, :\mathcal C \mathcal^\dagger =\mathbf. By acting on the particle twice with the \mathcal operator, : \mathcal^2 , \psi\rangle = \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
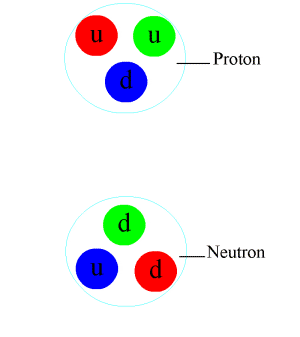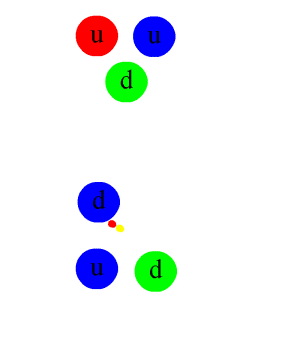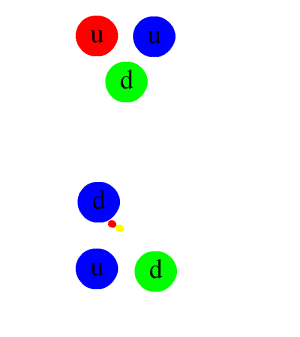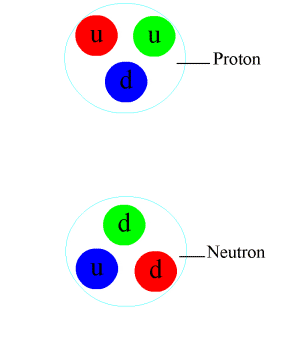
Meson
In particle physics, a meson () is a type of hadronic subatomic particle composed of an equal number of quarks and antiquarks, usually one of each, bound together by the strong interaction. Because mesons are composed of quark subparticles, they have a meaningful physical size, a diameter of roughly one femtometre (10 m), which is about 0.6 times the size of a proton or neutron. All mesons are unstable, with the longest-lived lasting for only a few tenths of a nanosecond. Heavier mesons decay to lighter mesons and ultimately to stable electrons, neutrinos and photons. Outside the nucleus, mesons appear in nature only as short-lived products of very high-energy collisions between particles made of quarks, such as cosmic rays (high-energy protons and neutrons) and baryonic matter. Mesons are routinely produced artificially in cyclotrons or other particle accelerators in the collisions of protons, antiprotons, or other particles. Higher-energy (more massive) mesons were ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pions
In particle physics, a pion (, ) or pi meson, denoted with the Greek letter pi (), is any of three subatomic particles: , , and . Each pion consists of a quark and an antiquark and is therefore a meson. Pions are the lightest mesons and, more generally, the lightest hadrons. They are unstable, with the charged pions and decaying after a mean lifetime of 26.033 nanoseconds ( seconds), and the neutral pion decaying after a much shorter lifetime of 85 attoseconds ( seconds). Charged pions most often decay into muons and muon neutrinos, while neutral pions generally decay into gamma rays. The exchange of virtual pions, along with vector, rho and omega mesons, provides an explanation for the residual strong force between nucleons. Pions are not produced in radioactive decay, but commonly are in high-energy collisions between hadrons. Pions also result from some matter–antimatter annihilation events. All types of pions are also produced in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pi Meson
In particle physics, a pion (, ) or pi meson, denoted with the Greek letter pi (), is any of three subatomic particles: , , and . Each pion consists of a quark and an antiquark and is therefore a meson. Pions are the lightest mesons and, more generally, the lightest hadrons. They are unstable, with the charged pions and decaying after a mean lifetime of 26.033 nanoseconds ( seconds), and the neutral pion decaying after a much shorter lifetime of 85 attoseconds ( seconds). Charged pions most often decay into muons and muon neutrinos, while neutral pions generally decay into gamma rays. The exchange of virtual pions, along with vector, rho and omega mesons, provides an explanation for the residual strong force between nucleons. Pions are not produced in radioactive decay, but commonly are in high-energy collisions between hadrons. Pions also result from some matter–antimatter annihilation events. All types of pions are also produced in natural proce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Charge Conjugation
In physics, charge conjugation is a transformation that switches all particles with their corresponding antiparticles, thus changing the sign of all charges: not only electric charge but also the charges relevant to other forces. The term C-symmetry is an abbreviation of the phrase "charge conjugation symmetry", and is used in discussions of the symmetry of physical laws under charge-conjugation. Other important discrete symmetries are P-symmetry (parity) and T-symmetry (time reversal). These discrete symmetries, C, P and T, are symmetries of the equations that describe the known fundamental forces of nature: electromagnetism, gravity, the strong and the weak interactions. Verifying whether some given mathematical equation correctly models nature requires giving physical interpretation not only to continuous symmetries, such as motion in time, but also to its discrete symmetries, and then determining whether nature adheres to these symmetries. Unlike the continuous symm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Number
In quantum physics and chemistry, quantum numbers are quantities that characterize the possible states of the system. To fully specify the state of the electron in a hydrogen atom, four quantum numbers are needed. The traditional set of quantum numbers includes the principal, azimuthal, magnetic, and spin quantum numbers. To describe other systems, different quantum numbers are required. For subatomic particles, one needs to introduce new quantum numbers, such as the flavour of quarks, which have no classical correspondence. Quantum numbers are closely related to eigenvalues of observables. When the corresponding observable commutes with the Hamiltonian of the system, the quantum number is said to be " good", and acts as a constant of motion in the quantum dynamics. History Electronic quantum numbers In the era of the old quantum theory, starting from Max Planck's proposal of quanta in his model of blackbody radiation (1900) and Albert Einstein's adaptation o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." It is one of the most fundamental scientific disciplines. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics. (...) You will come to see physics as a towering achievement of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenstate
In quantum physics, a quantum state is a mathematical entity that embodies the knowledge of a quantum system. Quantum mechanics specifies the construction, evolution, and measurement of a quantum state. The result is a prediction for the system represented by the state. Knowledge of the quantum state, and the rules for the system's evolution in time, exhausts all that can be known about a quantum system. Quantum states may be defined differently for different kinds of systems or problems. Two broad categories are * wave functions describing quantum systems using position or momentum variables and * the more abstract vector quantum states. Historical, educational, and application-focused problems typically feature wave functions; modern professional physics uses the abstract vector states. In both categories, quantum states divide into pure versus mixed states, or into coherent states and incoherent states. Categories with special properties include stationary states for time ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Total Angular Momentum Quantum Number
In quantum mechanics, the total angular momentum quantum number parametrises the total angular momentum of a given particle, by combining its orbital angular momentum and its intrinsic angular momentum (i.e., its spin). If s is the particle's spin angular momentum and ℓ its orbital angular momentum vector, the total angular momentum j is \mathbf j = \mathbf s + \boldsymbol ~. The associated quantum number is the main total angular momentum quantum number ''j''. It can take the following range of values, jumping only in integer steps: \vert \ell - s\vert \le j \le \ell + s where ''ℓ'' is the azimuthal quantum number (parameterizing the orbital angular momentum) and ''s'' is the spin quantum number (parameterizing the spin). The relation between the total angular momentum vector j and the total angular momentum quantum number ''j'' is given by the usual relation (see angular momentum quantum number) \Vert \mathbf j \Vert = \sqrt \, \hbar The vector's ''z''-projection is giv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Term Symbol
In atomic physics, a term symbol is an abbreviated description of the total spin and orbital angular momentum quantum numbers of the electrons in a multi-electron atom. So while the word ''symbol'' suggests otherwise, it represents an actual ''value'' of a physical quantity. For a given electron configuration of an atom, its state depends also on its total angular momentum, including spin and orbital components, which are specified by the term symbol. The usual atomic term symbols assume angular momentum coupling#LS coupling, LS coupling (also known as Russell–Saunders coupling) in which the all-electron total quantum numbers for orbital (''L''), spin (''S'') and total (''J'') angular momenta are good quantum numbers. In the terminology of atomic spectroscopy, ''L'' and ''S'' together specify a term; ''L'', ''S'', and ''J'' specify a level; and ''L'', ''S'', ''J'' and the magnetic quantum number ''M''''J'' specify a state. The conventional term symbol has the form 2''S''+1''L'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectroscopic Notation
Spectroscopic notation provides a way to specify atomic ionization states, atomic orbitals, and molecular orbitals. Ionization states Spectroscopists customarily refer to the spectrum arising from a given ionization state of a given element by the element's symbol followed by a Roman numeral. The numeral I is used for spectral lines associated with the neutral element, II for those from the first ionization state, III for those from the second ionization state, and so on. For example, "He I" denotes lines of neutral helium, and "C IV" denotes lines arising from the third ionization state, C3+, of carbon. This notation is used for example to retrieve data from thNIST Atomic Spectrum Database Atomic and molecular orbitals Before atomic orbitals were understood, spectroscopists discovered various distinctive series of spectral lines in atomic spectra, which they identified by letters. These letters were later associated with the azimuthal quantum number, ''ℓ''. The let ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermion
In particle physics, a fermion is a subatomic particle that follows Fermi–Dirac statistics. Fermions have a half-integer spin (spin 1/2, spin , Spin (physics)#Higher spins, spin , etc.) and obey the Pauli exclusion principle. These particles include all quarks and leptons and all composite particles made of an even and odd, odd number of these, such as all baryons and many atoms and atomic nucleus, nuclei. Fermions differ from bosons, which obey Bose–Einstein statistics. Some fermions are elementary particles (such as electrons), and some are composite particles (such as protons). For example, according to the spin-statistics theorem in Theory of relativity, relativistic quantum field theory, particles with integer Spin (physics), spin are bosons. In contrast, particles with half-integer spin are fermions. In addition to the spin characteristic, fermions have another specific property: they possess conserved baryon or lepton quantum numbers. Therefore, what is usually referr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Momentum Quantum Number
In quantum mechanics, the azimuthal quantum number is a quantum number for an atomic orbital that determines its angular momentum operator, orbital angular momentum and describes aspects of the angular shape of the orbital. The azimuthal quantum number is the second of a set of quantum numbers that describe the unique quantum state of an electron (the others being the principal quantum number , the magnetic quantum number , and the spin quantum number ). For a given value of the principal quantum number (''electron shell''), the possible values of are the integers from 0 to . For instance, the shell has only orbitals with \ell=0, and the shell has only orbitals with \ell=0, and \ell=1. For a given value of the azimuthal quantum number , the possible values of the magnetic quantum number are the integers from to , including 0. In addition, the spin quantum number can take two distinct values. The set of orbitals associated with a particular value of are som ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |