|
Böhmer Integral
In mathematics, a Böhmer integral is an integral introduced by generalizing the Fresnel integrals. There are two versions, given by \begin \operatorname(x,\alpha) &= \int_x^\infty t^ \cos(t) \, dt \\ ex\operatorname(x,\alpha) &= \int_x^\infty t^ \sin(t) \, dt \end Consequently, Fresnel integrals can be expressed in terms of the Böhmer integrals as \begin \operatorname(y) &= \frac1-\frac1\cdot\operatorname\left(\frac1,y^2\right) \\ ex\operatorname(y) &= \frac1-\frac1\cdot\operatorname\left(\frac1,y^2\right) \end The sine integral and cosine integral In mathematics, trigonometric integrals are a family of nonelementary integrals involving trigonometric functions. Sine integral The different sine integral definitions are \operatorname(x) = \int_0^x\frac\,dt \operatorname(x) = -\int ... can also be expressed in terms of the Böhmer integrals \begin \operatorname(x) &= \frac - \operatorname(x,0) \\ ex\operatorname(x) &= \frac -\operatorname(x,0) \end References * * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral
In mathematics, an integral is the continuous analog of a Summation, sum, which is used to calculate area, areas, volume, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental operations of calculus,Integral calculus is a very well established mathematical discipline for which there are many sources. See and , for example. the other being Derivative, differentiation. Integration was initially used to solve problems in mathematics and physics, such as finding the area under a curve, or determining displacement from velocity. Usage of integration expanded to a wide variety of scientific fields thereafter. A definite integral computes the signed area of the region in the plane that is bounded by the Graph of a function, graph of a given Function (mathematics), function between two points in the real line. Conventionally, areas above the horizontal Coordinate axis, axis of the plane are positive while areas below are n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
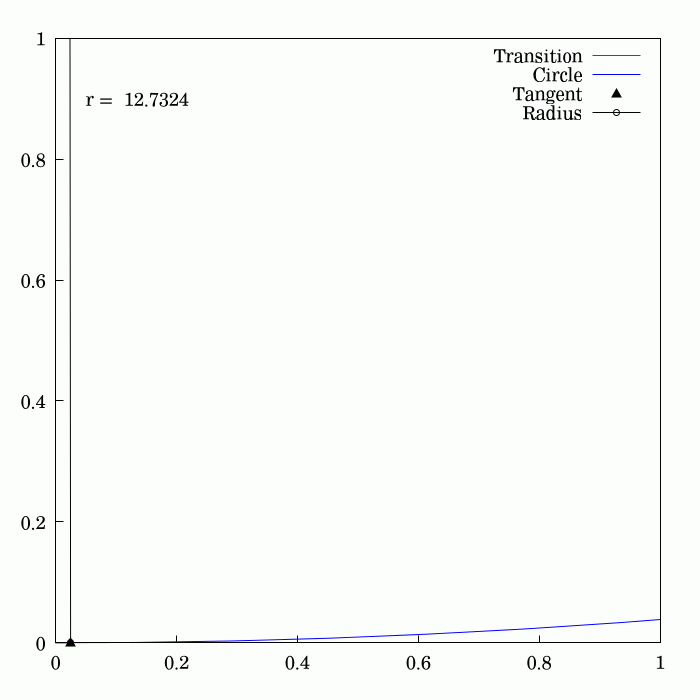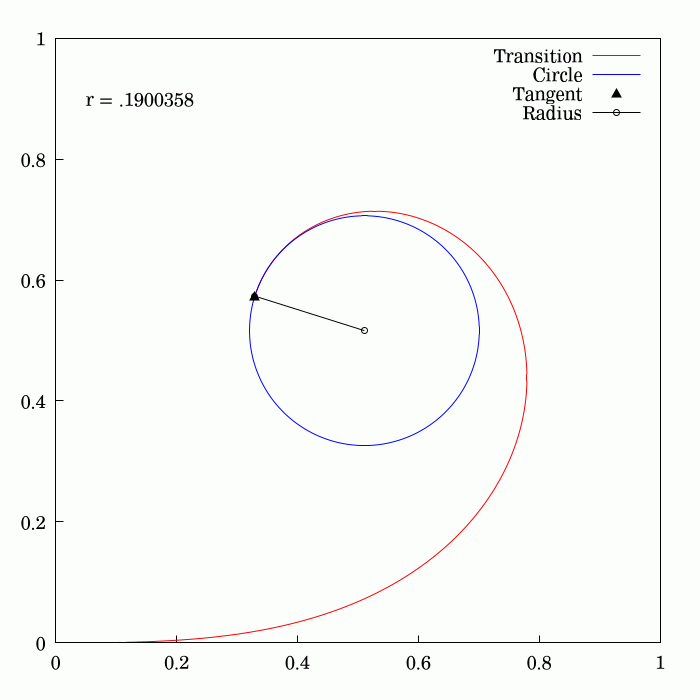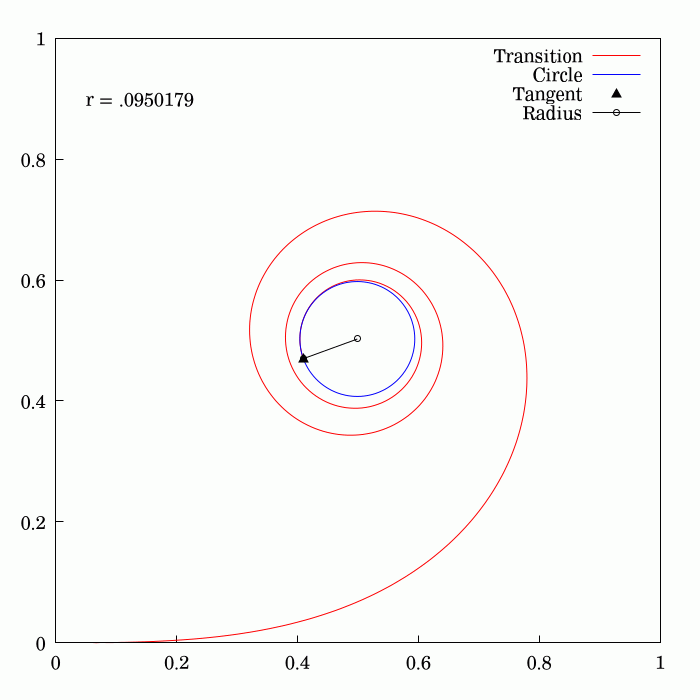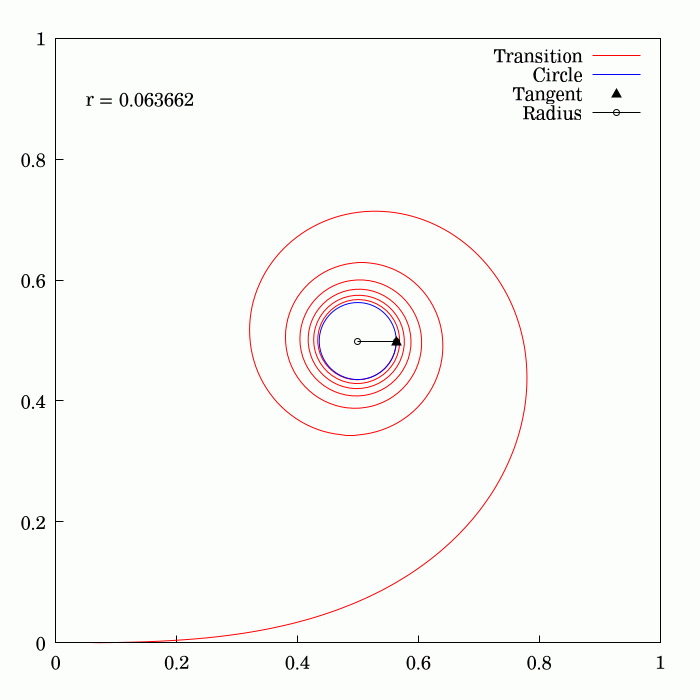
Fresnel Integral
250px, Plots of and . The maximum of is about . If the integrands of and were defined using instead of , then the image would be scaled vertically and horizontally (see below). The Fresnel integrals and are two transcendental functions named after Augustin-Jean Fresnel that are used in optics and are closely related to the error function (). They arise in the description of near-field Fresnel diffraction phenomena and are defined through the following integral representations: S(x) = \int_0^x \sin\left(t^2\right)\,dt, \quad C(x) = \int_0^x \cos\left(t^2\right)\,dt. The parametric curve is the Euler spiral or clothoid, a curve whose curvature varies linearly with arclength. The term Fresnel integral may also refer to the complex definite integral \int_^\infty e^ dx = \sqrte^ where is real and positive; this can be evaluated by closing a contour in the complex plane and applying Cauchy's integral theorem. Definition 250px, Fresnel integrals with arguments in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sine Integral
In mathematics, trigonometric integrals are a indexed family, family of nonelementary integrals involving trigonometric functions. Sine integral The different sine integral definitions are \operatorname(x) = \int_0^x\frac\,dt \operatorname(x) = -\int_x^\infty\frac\,dt~. Note that the integrand \frac is the sinc function, and also the zeroth Bessel function#Spherical Bessel functions: jn.2C yn, spherical Bessel function. Since is an even function, even entire function (holomorphic over the entire complex plane), is entire, odd, and the integral in its definition can be taken along Cauchy's integral theorem, any path connecting the endpoints. By definition, is the antiderivative of whose value is zero at , and is the antiderivative whose value is zero at . Their difference is given by the Dirichlet integral, \operatorname(x) - \operatorname(x) = \int_0^\infty\frac\,dt = \frac \quad \text \quad \operatorname(x) = \frac + \operatorname(x) ~. In signal processing, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cosine Integral
In mathematics, trigonometric integrals are a family of nonelementary integrals involving trigonometric functions. Sine integral The different sine integral definitions are \operatorname(x) = \int_0^x\frac\,dt \operatorname(x) = -\int_x^\infty\frac\,dt~. Note that the integrand \frac is the sinc function, and also the zeroth spherical Bessel function. Since is an even entire function (holomorphic over the entire complex plane), is entire, odd, and the integral in its definition can be taken along any path connecting the endpoints. By definition, is the antiderivative of whose value is zero at , and is the antiderivative whose value is zero at . Their difference is given by the Dirichlet integral, \operatorname(x) - \operatorname(x) = \int_0^\infty\frac\,dt = \frac \quad \text \quad \operatorname(x) = \frac + \operatorname(x) ~. In signal processing, the oscillations of the sine integral cause overshoot and ringing artifacts when using the sinc filter, and f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |