|
Betweenness Centrality
In graph theory, betweenness centrality is a measure of centrality in a graph based on shortest paths. For every pair of vertices in a connected graph, there exists at least one shortest path between the vertices, that is, there exists at least one path such that either the number of edges that the path passes through (for unweighted graphs) or the sum of the weights of the edges (for weighted graphs) is minimized. Betweenness centrality was devised as a general measure of centrality: it applies to a wide range of problems in network theory, including problems related to social networks, biology, transport and scientific cooperation. Although earlier authors have intuitively described centrality as based on betweenness, gave the first formal definition of betweenness centrality. Betweenness centrality finds wide application in network theory; it represents the degree to which nodes stand between each other. For example, in a telecommunications network, a node with higher b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Betweenness
Graph may refer to: Mathematics *Graph (discrete mathematics), a structure made of vertices and edges **Graph theory, the study of such graphs and their properties *Graph (topology), a topological space resembling a graph in the sense of discrete mathematics *Graph of a function *Graph of a relation *Graph paper *Chart, a means of representing data (also called a graph) Computing *Graph (abstract data type), an abstract data type representing relations or connections *graph (Unix), Unix command-line utility *Conceptual graph, a model for knowledge representation and reasoning *Microsoft Graph, a Microsoft API developer platform that connects multiple services and devices Other uses *HMS Graph, HMS ''Graph'', a submarine of the UK Royal Navy See also *Complex network *Graf *Graff (other) *Graph database *Grapheme, in linguistics *Graphemics *Graphic (other) *-graphy (suffix from the Greek for "describe," "write" or "draw") *List of information graphics soft ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Big O Notation
Big ''O'' notation is a mathematical notation that describes the asymptotic analysis, limiting behavior of a function (mathematics), function when the Argument of a function, argument tends towards a particular value or infinity. Big O is a member of a #Related asymptotic notations, family of notations invented by German mathematicians Paul Gustav Heinrich Bachmann, Paul Bachmann, Edmund Landau, and others, collectively called Bachmann–Landau notation or asymptotic notation. The letter O was chosen by Bachmann to stand for '':wikt:Ordnung#German, Ordnung'', meaning the order of approximation. In computer science, big O notation is used to Computational complexity theory, classify algorithms according to how their run time or space requirements grow as the input size grows. In analytic number theory, big O notation is often used to express a bound on the difference between an arithmetic function, arithmetical function and a better understood approximation; one well-known exam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Connectivity (graph Theory)
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements (nodes or edges) that need to be removed to separate the remaining nodes into two or more Connected component (graph theory), isolated subgraphs. It is closely related to the theory of flow network, network flow problems. The connectivity of a graph is an important measure of its resilience as a network. Connected vertices and graphs In an undirected graph , two vertex (graph theory), vertices and are called connected if contains a Path (graph theory), path from to . Otherwise, they are called disconnected. If the two vertices are additionally connected by a path of length (that is, they are the endpoints of a single edge), the vertices are called adjacent. A Graph (discrete mathematics), graph is said to be connected if every pair of vertices in the graph is connected. This means that there is a Path (graph theory), path between every ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strahler Number
In mathematics, the Strahler number or Horton–Strahler number of a mathematical tree (graph theory), tree is a numerical measure of its branching complexity. These numbers were first developed in hydrology, as a way of measuring the complexity of rivers and streams, by and . In this application, they are referred to as the Strahler stream order and are used to define stream size based on a hierarchy of tributary, tributaries. The same numbers also arise in the analysis of L-systems and of hierarchical biological structures such as (biological) trees and animal respiratory and circulatory systems, in register allocation for compiler, compilation of high-level programming languages and in the analysis of social networks. Definition All trees in this context are directed graphs, oriented from the root towards the leaves; in other words, they are Arborescence (graph theory), arborescences. The degree (graph theory), degree of a node in a tree is just its number of children. One may ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topological Complexity
In mathematics, topological complexity of a topological space ''X'' (also denoted by TC(''X'')) is a topological invariant closely connected to the motion planning problem, introduced by Michael Farber in 2003. Definition Let ''X'' be a topological space and PX=\ be the space of all continuous paths in ''X''. Define the projection \pi: PX\to\,X\times X by \pi(\gamma)=(\gamma(0), \gamma(1)). The topological complexity is the minimal number ''k'' such that *there exists an open cover \_^k of X\times X, *for each i=1,\ldots,k, there exists a local section s_i:\,U_i\to\, PX. Examples *The topological complexity: TC(''X'') = 1 if and only if ''X'' is contractible. *The topological complexity of the sphere S^n is 2 for ''n'' odd and 3 for ''n'' even. For example, in the case of the circle S^1, we may define a path between two points to be the geodesic between the points, if it is unique. Any pair of antipodal points can be connected by a counter-clockwise path. *If F(\R^m,n) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Social Capital
Social capital is a concept used in sociology and economics to define networks of relationships which are productive towards advancing the goals of individuals and groups. It involves the effective functioning of social groups through interpersonal relationships, a shared sense of identity, a shared understanding, shared norms, shared values, trust, cooperation, and reciprocity. Some have described it as a form of capital that produces public goods for a common purpose, although this does not align with how it has been measured. Social capital has been used to explain the improved performance of diverse groups, the growth of entrepreneurial firms, superior managerial performance, enhanced supply chain relations, the value derived from strategic alliances, and the evolution of communities. History While it has been suggested that the term ''social capital'' was in intermittent use from about 1890, before becoming widely used in the late 1990s, the earliest credited us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interpersonal Ties
In social network analysis and mathematical sociology, interpersonal ties are defined as information-carrying connections between people. Interpersonal ties, generally, come in three varieties: ''strong'', ''weak'' or ''absent''. Weak social ties, it is argued, are responsible for the majority of the embeddedness and structure of social networks in society as well as the transmission of information through these networks. Specifically, more novel information flows to individuals through weak rather than strong ties. Because our close friends tend to move in the same circles that we do, the information they receive overlaps considerably with what we already know. Acquaintances, by contrast, know people that we do not, and thus receive more novel information. Included in the definition of ''absent ties'', according to the American sociologist Mark Granovetter, are those relationships (or ties) without substantial significance, such as "nodding" relationships between people livin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Online Social Networks
A social network is a social structure consisting of a set of social actors (such as individuals or organizations), networks of dyadic ties, and other social interactions between actors. The social network perspective provides a set of methods for analyzing the structure of whole social entities along with a variety of theories explaining the patterns observed in these structures. The study of these structures uses social network analysis to identify local and global patterns, locate influential entities, and examine dynamics of networks. For instance, social network analysis has been used in studying the spread of misinformation on social media platforms or analyzing the influence of key figures in social networks. Social networks and the analysis of them is an inherently interdisciplinary academic field which emerged from social psychology, sociology, statistics, and graph theory. Georg Simmel authored early structural theories in sociology emphasizing the dynamics of triads ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
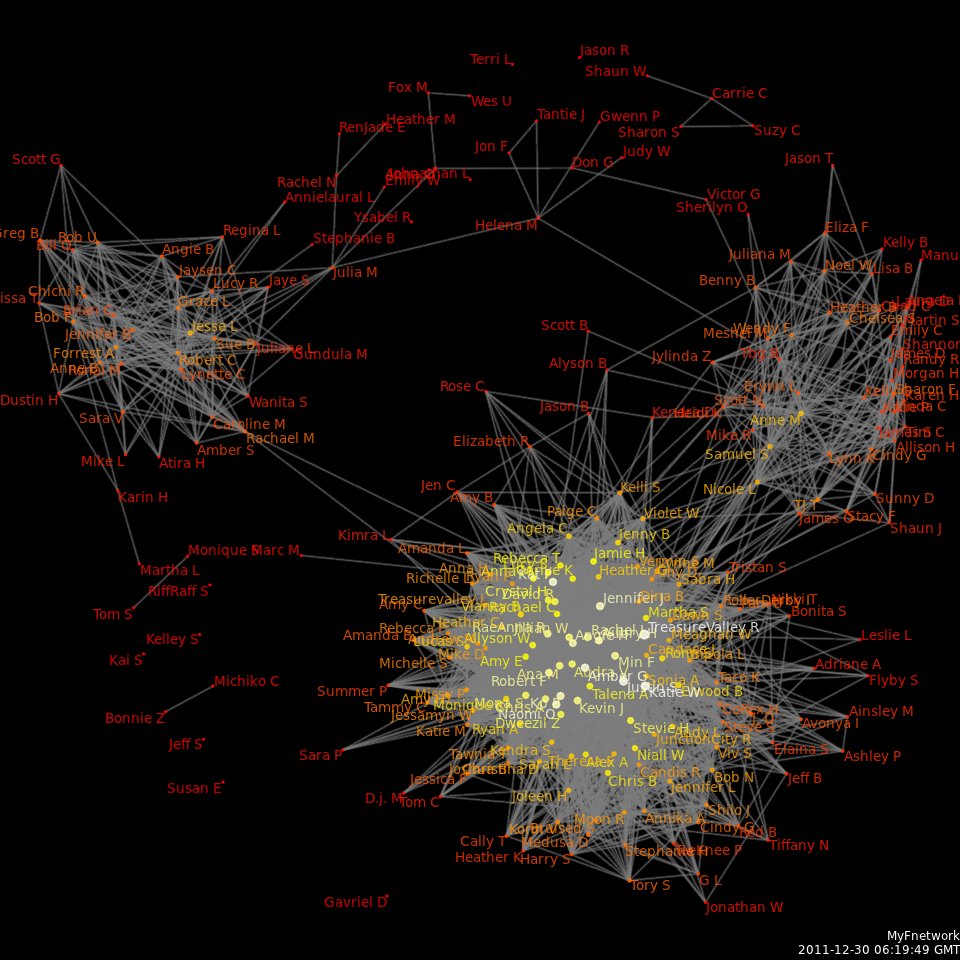
Social Network Analysis
Social network analysis (SNA) is the process of investigating social structures through the use of networks and graph theory. It characterizes networked structures in terms of ''nodes'' (individual actors, people, or things within the network) and the ''ties'', ''edges'', or ''links'' (relationships or interactions) that connect them. Examples of social structures commonly visualized through social network analysis include social media networks, meme proliferation, information circulation, friendship and acquaintance networks, business networks, knowledge networks, difficult working relationships, collaboration graphs, kinship, disease transmission, and sexual relationships. These networks are often visualized through '' sociograms'' in which nodes are represented as points and ties are represented as lines. These visualizations provide a means of qualitatively assessing networks by varying the visual representation of their nodes and edges to reflect attributes of inter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Breadth-first Search
Breadth-first search (BFS) is an algorithm for searching a tree data structure for a node that satisfies a given property. It starts at the tree root and explores all nodes at the present depth prior to moving on to the nodes at the next depth level. Extra memory, usually a queue, is needed to keep track of the child nodes that were encountered but not yet explored. For example, in a chess endgame, a chess engine may build the game tree from the current position by applying all possible moves and use breadth-first search to find a win position for White. Implicit trees (such as game trees or other problem-solving trees) may be of infinite size; breadth-first search is guaranteed to find a solution node if one exists. In contrast, (plain) depth-first search (DFS), which explores the node branch as far as possible before backtracking and expanding other nodes, may get lost in an infinite branch and never make it to the solution node. Iterative deepening depth-first search ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Johnson's Algorithm
Johnson's algorithm is a way to find the shortest paths between all pairs of vertices in an edge-weighted directed graph. It allows some of the edge weights to be negative numbers, but no negative-weight cycles may exist. It works by using the Bellman–Ford algorithm to compute a transformation of the input graph that removes all negative weights, allowing Dijkstra's algorithm to be used on the transformed graph.. Section 25.3, "Johnson's algorithm for sparse graphs", pp. 636–640.. It is named after Donald B. Johnson, who first published the technique in 1977. A similar reweighting technique is also used in a version of the successive shortest paths algorithm for the minimum cost flow problem due to Edmonds and Karp, as well as in Suurballe's algorithm for finding two disjoint paths of minimum total length between the same two vertices in a graph with non-negative edge weights.. Algorithm description Johnson's algorithm consists of the following steps: #First, a ne ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Floyd–Warshall Algorithm
In computer science, the Floyd–Warshall algorithm (also known as Floyd's algorithm, the Roy–Warshall algorithm, the Roy–Floyd algorithm, or the WFI algorithm) is an algorithm for finding shortest paths in a directed weighted graph with positive or negative edge weights (but with no negative cycles). See in particular Section 26.2, "The Floyd–Warshall algorithm", pp. 558–565 and Section 26.4, "A general framework for solving path problems in directed graphs", pp. 570–576. A single execution of the algorithm will find the lengths (summed weights) of shortest paths between all pairs of vertices. Although it does not return details of the paths themselves, it is possible to reconstruct the paths with simple modifications to the algorithm. Versions of the algorithm can also be used for finding the transitive closure of a relation R, or (in connection with the Schulze voting system) widest paths between all pairs of vertices in a weighted graph. History and nam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |