|
Beatty Sequence
In mathematics, a Beatty sequence (or homogeneous Beatty sequence) is the sequence of integers found by taking the floor of the positive multiples of a positive irrational number. Beatty sequences are named after Samuel Beatty, who wrote about them in 1926. Rayleigh's theorem, named after Lord Rayleigh, states that the complement of a Beatty sequence, consisting of the positive integers that are not in the sequence, is itself a Beatty sequence generated by a different irrational number. Beatty sequences can also be used to generate Sturmian words. Definition Any irrational number r that is greater than one generates the Beatty sequence \mathcal_r = \bigl\ The two irrational numbers r and s = r/(r-1) naturally satisfy the equation 1/r + 1/s = 1. The two Beatty sequences \mathcal_r and \mathcal_s that they generate form a ''pair of complementary Beatty sequences''. Here, "complementary" means that every positive integer belongs to exactly one of these two sequences. Examples When ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
11 (number)
11 (eleven) is the natural number following 10 and preceding 12 (number), 12. It is the smallest number whose name has three syllables. Name "Eleven" derives from the Old English ', which is first attested in Bede's late 9th-century ''Ecclesiastical History of the English People''. It has cognates in every Germanic language (for example, German ), whose Proto-Germanic language, Proto-Germanic ancestor has been linguistic reconstruction, reconstructed as , from the prefix (adjectival "1 (number), one") and suffix , of uncertain meaning. It is sometimes compared with the Lithuanian language, Lithuanian ', though ' is used as the suffix for all numbers from 11 to 19. The Old English form has closer cognates in Old Frisian, Old Saxon, Saxon, and Old Norse, Norse, whose ancestor has been reconstructed as . This was formerly thought to be derived from Proto-Germanic ("10 (number), ten"); it is now sometimes connected with or ("left; remaining"), with the implicit meaning that "one is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
5 (number)
5 (five) is a number, numeral and digit. It is the natural number In mathematics, the natural numbers are the numbers 0, 1, 2, 3, and so on, possibly excluding 0. Some start counting with 0, defining the natural numbers as the non-negative integers , while others start with 1, defining them as the positive in ..., and cardinal number, following 4 and preceding 6, and is a prime number. Humans, and many other animals, have 5 Digit (anatomy), digits on their Limb (anatomy), limbs. Mathematics 5 is a Fermat prime, a Mersenne prime exponent, as well as a Fibonacci number. 5 is the first congruent number, as well as the length of the hypotenuse of the smallest integer-sided right triangle, making part of the smallest Pythagorean triple (3, 4, 5). 5 is the first safe prime and the first good prime. 11 forms the first pair of sexy primes with 5. 5 is the second Fermat number, Fermat prime, of a total of five known Fermat primes. 5 is also the first of three known Wilso ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
2 (number)
2 (two) is a number, numeral and digit. It is the natural number following 1 and preceding 3. It is the smallest and the only even prime number. Because it forms the basis of a duality, it has religious and spiritual significance in many cultures. Mathematics The number 2 is the second natural number after 1. Each natural number, including 2, is constructed by succession, that is, by adding 1 to the previous natural number. 2 is the smallest and the only even prime number, and the first Ramanujan prime. It is also the first superior highly composite number, and the first colossally abundant number. An integer is determined to be even if it is divisible by two. When written in base 10, all multiples of 2 will end in 0, 2, 4, 6, or 8; more generally, in any even base, even numbers will end with an even digit. A digon is a polygon with two sides (or edges) and two vertices. Two distinct points in a plane are always sufficient to define a unique line in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
29 (number)
29 (twenty-nine) is the natural number following 28 and preceding 30. It is a prime number. 29 is the number of days February has on a leap year. Mathematics 29 is the tenth prime number. Integer properties 29 is the fifth primorial prime, like its twin prime 31. 29 is the smallest positive whole number that cannot be made from the numbers \, using each digit exactly once and using only addition, subtraction, multiplication, and division. None of the first twenty-nine natural numbers have more than two different prime factors (in other words, this is the longest such consecutive sequence; the first sphenic number or triprime, 30 is the product of the first three primes 2, 3, and 5). 29 is also, * the sum of three consecutive squares, 22 + 32 + 42. * the sixth Sophie Germain prime. * a Lucas prime, a Pell prime, and a tetranacci number. * an Eisenstein prime with no imaginary part and real part of the form 3n − 1. * a Markov number, appearing in the solution ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
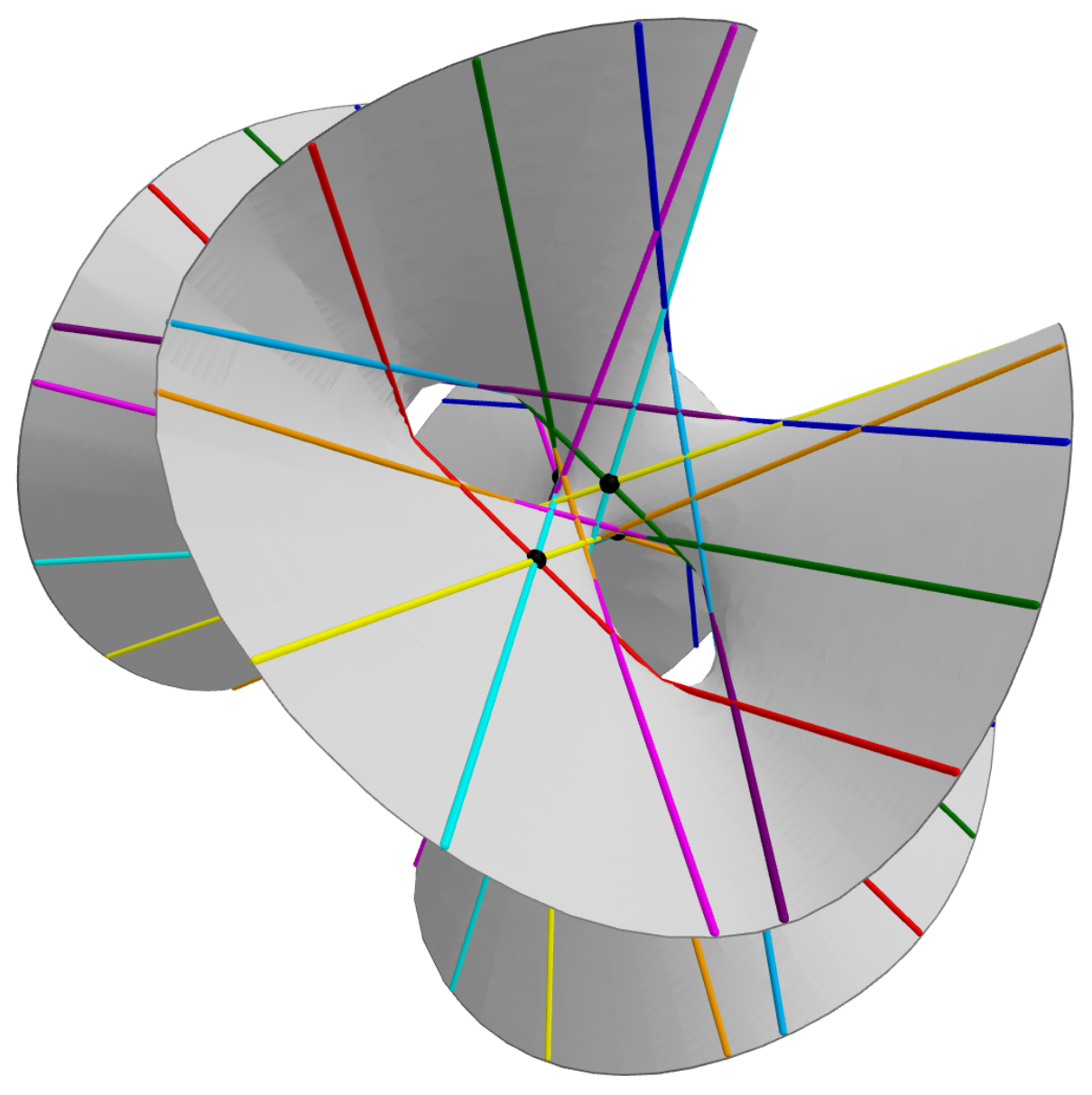 |
27 (number)
27 (twenty-seven) is the natural number following 26 (number), 26 and preceding 28 (number), 28. Mathematics Including the null-motif, there are 27 distinct Network motif, hypergraph motifs. There are exactly 27 lines on a cubic surface, ''twenty-seven straight lines'' on a smooth cubic surface, which give a basis of the fundamental representation of E6 (mathematics), Lie algebra \mathrm . The unique simple formally real Jordan algebra, the exceptional Jordan algebra of self-adjoint Square matrix, 3 by 3 matrices of quaternions, is 27-dimensional; its automorphism group is the 52-dimensional exceptional Lie algebra \mathrm . There are twenty-seven sporadic groups, if the Tits group, ''non-strict'' group of Lie type \mathrm (with an Faithful representation, irreducible representation that is twice that of \mathrm in 104 dimensions) is included. In Robin's theorem for the Riemann hypothesis, twenty-seven integers fail to hold \sigma(n) < e^\gamma n \log \log n for va ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
25 (number)
25 (twenty-five) is the natural number following 24 and preceding 26. In mathematics It is a square number, being 52 = 5 × 5, and hence the third non-unitary square prime of the form ''p''2. It is one of two two-digit numbers whose square and higher powers of the number also ends in the same last two digits, e.g., 252 = 625; the other is 76. 25 has an even aliquot sum of 6, which is itself the first even and perfect number root of an aliquot sequence; not ending in ( 1 and 0). It is the smallest square that is also a sum of two (non-zero) squares: 25 = 32 + 42. Hence, it often appears in illustrations of the Pythagorean theorem. 25 is the sum of the five consecutive single-digit odd natural numbers 1, 3, 5, 7, and 9. 25 is a centered octagonal number, a centered square number, a centered octahedral number, and an automorphic number. 25 percent (%) is equal to . It is the smallest decimal Friedman number as it can be expressed by its own digits: 52. It ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
24 (number)
24 (twenty-four) is the natural number following 23 (number), 23 and preceding 25 (number), 25. It is equal to two dozen and one sixth of a Gross (unit), gross. In mathematics 24 is an Parity (mathematics), even composite number, a highly composite number, an abundant number, a practical number, and a congruent number. The many ways 24 can be constructed inspired a children's mathematical game involving the use of any of the four standard operations on four numbers on a card to get 24 (see 24 (puzzle), 24 Game). 24 is also part of the only nontrivial solution pair to the cannonball problem, and the kissing number in Four-dimensional space, 4-dimensional space. An icositetragon is a regular polygon with 24 sides. A tesseract has 24 two-dimensional square faces. In religion *In Christian apocalyptic literature it represents the complete Church, being the sum of the 12 tribes of Israel and the 12 Apostles in the New Testament, Apostles of the Lamb of God. For example, in ''The Boo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
22 (number)
22 (twenty-two) is the natural number following 21 and preceding 23. In mathematics 22 is a semiprime, a Smith number, and an Erdős–Woods number. \frac = 3.14\ldots is a commonly used approximation of the irrational number , the ratio of the circumference of a circle to its diameter. 22 can read as "two twos", which is the only fixed point of John Conway's look-and-say function. The number 22 appears prominently within sporadic groups. The Mathieu group M22 is one of 26 sporadic finite simple groups, defined as the 3-transitive permutation representation on 22 points. There are also 22 regular complex apeirohedra. 22 has been proven to be a Lychrel number in base 2, since after 4 steps it reaches 10110100, after 8 steps it reaches 1011101000, after 12 steps it reaches 101111010000, and in general after steps it reaches a number consisting of 10, followed by ones, followed by 01, followed by zeros. This number obviously cannot be a palindrome, and none of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
21 (number)
21 (twenty-one) is the natural number following 20 and preceding 22. The current century is the 21st century AD, under the Gregorian calendar. Mathematics Twenty-one is the fifth distinct semiprime, and the second of the form 3 \times q where q is a higher prime. It is a repdigit in quaternary (1114). Properties As a biprime with proper divisors 1, 3 and 7, twenty-one has a prime aliquot sum of 11 within an aliquot sequence containing only one composite number (21, 11, 1, 0). 21 is the first member of the second cluster of consecutive discrete semiprimes (21, 22), where the next such cluster is ( 33, 34, 35). There are 21 prime numbers with 2 digits. There are a total of 21 prime numbers between 100 and 200. 21 is the first Blum integer, since it is a semiprime with both its prime factors being Gaussian primes. While 21 is the sixth triangular number, it is also the sum of the divisors of the first five positive integers: \begin 1 & + 2 + 3 + 4 + 5 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
19 (number)
19 (nineteen) is the natural number following 18 (number), 18 and preceding 20 (number), 20. It is a prime number. Mathematics Nineteen is the eighth prime number. Number theory 19 forms a twin prime with 17 (number), 17, a cousin prime with 23 (number), 23, and a sexy prime with 13 (number), 13. 19 is the fifth Trinomial triangle#Central trinomial coefficients, central trinomial coefficient, and the maximum number of fourth powers needed to sum up to any natural number (see, Waring's problem). It is the number of Composition (combinatorics), compositions of 8 into distinct parts. 19 is the eighth strictly non-palindromic number in any Numeral system, base, following 11 (number), 11 and preceding 47 (number), 47. 19 is also the second octahedral number, after 6, and the sixth Heegner number. In the Engel expansion of pi, 19 is the seventh term following and preceding . The sum of the first terms preceding 17 (number), 17 is in equivalence with 19, where its prime Sequen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
17 (number)
17 (seventeen) is the natural number following 16 (number), 16 and preceding 18 (number), 18. It is a prime number. 17 was described at MIT as "the least random number", according to the Jargon File. This is supposedly because, in a study where respondents were asked to choose a random number from 1 to 20, 17 was the most common choice. This study has been repeated a number of times. Mathematics 17 is a Leyland number and Leyland number#Leyland primes, Leyland prime, using 2 & 3 (23 + 32) and using 4 and 5, using 3 & 4 (34 - 43). 17 is a Fermat prime. 17 is one of six lucky numbers of Euler. Since seventeen is a Fermat prime, regular heptadecagons can be constructible polygon, constructed with a compass and unmarked ruler. This was proven by Carl Friedrich Gauss and ultimately led him to choose mathematics over philology for his studies. The minimum possible number of givens for a sudoku puzzle with a unique solution is 17. Geometric properties Two-dimensions *There are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |