|
Base Stock Model
The base stock model is a statistical model in inventory theory.W.H. Hopp, M. L. Spearman, Factory Physics, Waveland Press 2008 In this model inventory is refilled one unit at a time and demand is random. If there is only one replenishment, then the problem can be solved with the newsvendor model. Overview Assumptions # Products can be analyzed individually # Demands occur one at a time (no batch orders) # Unfilled demand is back-ordered (no lost sales) # Replenishment lead times are fixed and known # Replenishments are ordered one at a time # Demand is modeled by a continuous probability distribution Variables *L = Replenishment lead time *X = Demand during replenishment lead time *g(x) = probability density function of demand during lead time *G(x) = cumulative distribution function of demand during lead time *\theta = mean demand during lead time *h = cost to carry one unit of inventory for 1 year *b = cost to carry one unit of back-order for 1 year *r = reorder point *SS=r-\t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inventory Theory
Material theory (or more formally the mathematical theory of inventory and production) is the sub-specialty within operations research and operations management that is concerned with the design of production/inventory systems to minimize costs: it studies the decisions faced by firms and the military in connection with manufacturing, warehousing, supply chains, spare part allocation and so on and provides the mathematical foundation for logistics. The inventory control problem is the problem faced by a firm that must decide how much to order in each time period to meet demand for its products. The problem can be modeled using mathematical techniques of optimal control, dynamic programming and network optimization. The study of such models is part of inventory theory. Issues One issue is infrequent large orders vs. frequent small orders. Large orders will increase the amount of inventory on hand, which is costly, but may benefit from volume discounts. Frequent orders are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random
In common usage, randomness is the apparent or actual lack of pattern or predictability in events. A random sequence of events, symbols or steps often has no order and does not follow an intelligible pattern or combination. Individual random events are, by definition, unpredictable, but if the probability distribution is known, the frequency of different outcomes over repeated events (or "trials") is predictable.Strictly speaking, the frequency of an outcome will converge almost surely to a predictable value as the number of trials becomes arbitrarily large. Non-convergence or convergence to a different value is possible, but has probability zero. For example, when throwing two dice, the outcome of any particular roll is unpredictable, but a sum of 7 will tend to occur twice as often as 4. In this view, randomness is not haphazardness; it is a measure of uncertainty of an outcome. Randomness applies to concepts of chance, probability, and information entropy. The fields of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newsvendor Model
The newsvendor (or newsboy or single-periodWilliam J. Stevenson, Operations Management. 10th edition, 2009; page 581 or salvageable) model is a mathematical model in operations management and applied economics used to determine optimal inventory levels. It is (typically) characterized by fixed prices and uncertain demand for a perishable product. If the inventory level is q, each unit of demand above q is lost in potential sales. This model is also known as the ''newsvendor problem'' or ''newsboy problem'' by analogy with the situation faced by a newspaper vendor who must decide how many copies of the day's paper to stock in the face of uncertain demand and knowing that unsold copies will be worthless at the end of the day. History The mathematical problem appears to date from 1888 where Edgeworth used the central limit theorem to determine the optimal cash reserves to satisfy random withdrawals from depositors. According to Chen, Cheng, Choi and Wang (2016), the term "news ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Density Function
In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) can be interpreted as providing a ''relative likelihood'' that the value of the random variable would be close to that sample. Probability density is the probability per unit length, in other words, while the ''absolute likelihood'' for a continuous random variable to take on any particular value is 0 (since there is an infinite set of possible values to begin with), the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would be close to one sample compared to the other sample. In a more precise sense, the PDF is used to specify the probability of the random variable falling ''within a particular range of values'', as opposed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cumulative Distribution Function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x. Every probability distribution supported on the real numbers, discrete or "mixed" as well as continuous, is uniquely identified by an ''upwards continuous'' ''monotonic increasing'' cumulative distribution function F : \mathbb R \rightarrow ,1/math> satisfying \lim_F(x)=0 and \lim_F(x)=1. In the case of a scalar continuous distribution, it gives the area under the probability density function from minus infinity to x. Cumulative distribution functions are also used to specify the distribution of multivariate random variables. Definition The cumulative distribution function of a real-valued random variable X is the function given by where the right-hand side represents the probability that the random variable X takes on a value less ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reorder Point
The reorder point (ROP) is the level of inventory which triggers an action to replenish that particular inventory stock. It is a minimum amount of an item which a firm holds in stock, such that, when stock falls to this amount, the item must be reordered. It is normally calculated as the forecast usage during the replenishment lead time plus safety stock. In the EOQ (Economic Order Quantity) model, it was assumed that there is no time lag between ordering and procuring of materials. Continuous Review System The reorder point for replenishment of stock occurs when the level of inventory drops down to zero. In view of instantaneous replenishment of stock the level of inventory jumps to the original level from zero level. In real life situations one never encounters a zero lead time. There is always a time lag from the date of placing an order for material and the date on which materials are received. As a result the reorder point is always higher than zero, and if the firm places t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Safety Stock
Safety stock is a term used by logisticians to describe a level of extra stock that is maintained to mitigate risk of stockouts (shortfall in raw material or packaging) caused by uncertainties in supply and demand. Adequate safety stock levels permit business operations to proceed according to their plans.Monk, Ellen and Bret Wagner. Concepts in Enterprise Resource Planning. 3rd Edition. Boston: Course Technology Cengage Learning, 2009. Safety stock is held when uncertainty exists in demand, supply, or manufacturing yield, and serves as an insurance against stockouts. Safety stock is an additional quantity of an item held in the inventory to reduce the risk that the item will be out of stock. It acts as a buffer stock in case sales are greater than planned and/or the supplier is unable to deliver the additional units at the expected time. With a new product, safety stock can be used as a strategic tool until the company can judge how accurate its forecast is after the first few y ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Normal
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is : f(x) = \frac e^ The parameter \mu is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma is its standard deviation. The variance of the distribution is \sigma^2. A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal distrib ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probit
In probability theory and statistics, the probit function is the quantile function associated with the standard normal distribution. It has applications in data analysis and machine learning, in particular exploratory statistical graphics and specialized regression modeling of binary response variables. Mathematically, the probit is the inverse of the cumulative distribution function of the standard normal distribution, which is denoted as \Phi(z), so the probit is defined as :\operatorname(p) = \Phi^(p) \quad \text \quad p \in (0,1). Largely because of the central limit theorem, the standard normal distribution plays a fundamental role in probability theory and statistics. If we consider the familiar fact that the standard normal distribution places 95% of probability between −1.96 and 1.96, and is symmetric around zero, it follows that :\Phi(-1.96) = 0.025 = 1-\Phi(1.96).\,\! The probit function gives the 'inverse' computation, generating a value of a standard normal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
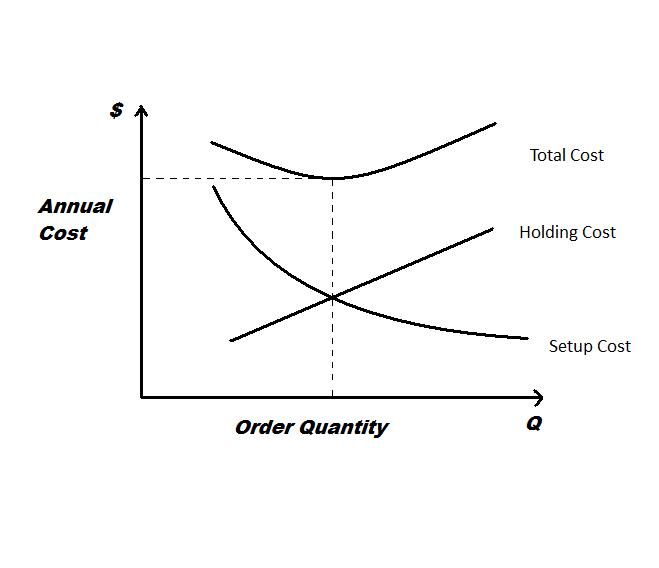
Economic Order Quantity
Economic Order Quantity (EOQ), also known as Economic Buying Quantity (EPQ), is the order quantity that minimizes the total holding costs and ordering costs in inventory management. It is one of the oldest classical production scheduling models. The model was developed by Ford W. Harris in 1913, but R. H. Wilson, a consultant who applied it extensively, and K. Andler are given credit for their in-depth analysis. Overview EOQ applies only when demand for a product is constant over the year and each new order is delivered in full when inventory reaches zero. There is a fixed cost for each order placed, regardless of the number of units ordered; an order is assumed to contain only 1 unit. There is also a cost for each unit held in storage, commonly known as holding cost, sometimes expressed as a percentage of the purchase cost of the item. While the EOQ formulation is straightforward there are factors such as transportation rates and quantity discounts to consider in actual appli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Economic Production Quantity
The economic production quantity model (also known as the EPQ model) determines the quantity a company or retailer should order to minimize the total inventory costs by balancing the inventory holding cost and average fixed ordering cost. The EPQ model was developed by E.W. Taft in 1918. This method is an extension of the economic order quantity model (also known as the EOQ model). The difference between these two methods is that the EPQ model assumes the company will produce its own quantity or the parts are going to be shipped to the company while they are being produced, therefore the orders are available or received in an incremental manner while the products are being produced. While the EOQ model assumes the order quantity arrives complete and immediately after ordering, meaning that the parts are produced by another company and are ready to be shipped when the order is placed. In some literature, "economic manufacturing quantity" model (EMQ) is used for "economic productio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newsvendor Model
The newsvendor (or newsboy or single-periodWilliam J. Stevenson, Operations Management. 10th edition, 2009; page 581 or salvageable) model is a mathematical model in operations management and applied economics used to determine optimal inventory levels. It is (typically) characterized by fixed prices and uncertain demand for a perishable product. If the inventory level is q, each unit of demand above q is lost in potential sales. This model is also known as the ''newsvendor problem'' or ''newsboy problem'' by analogy with the situation faced by a newspaper vendor who must decide how many copies of the day's paper to stock in the face of uncertain demand and knowing that unsold copies will be worthless at the end of the day. History The mathematical problem appears to date from 1888 where Edgeworth used the central limit theorem to determine the optimal cash reserves to satisfy random withdrawals from depositors. According to Chen, Cheng, Choi and Wang (2016), the term "news ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |