|
Barnes Interpolation
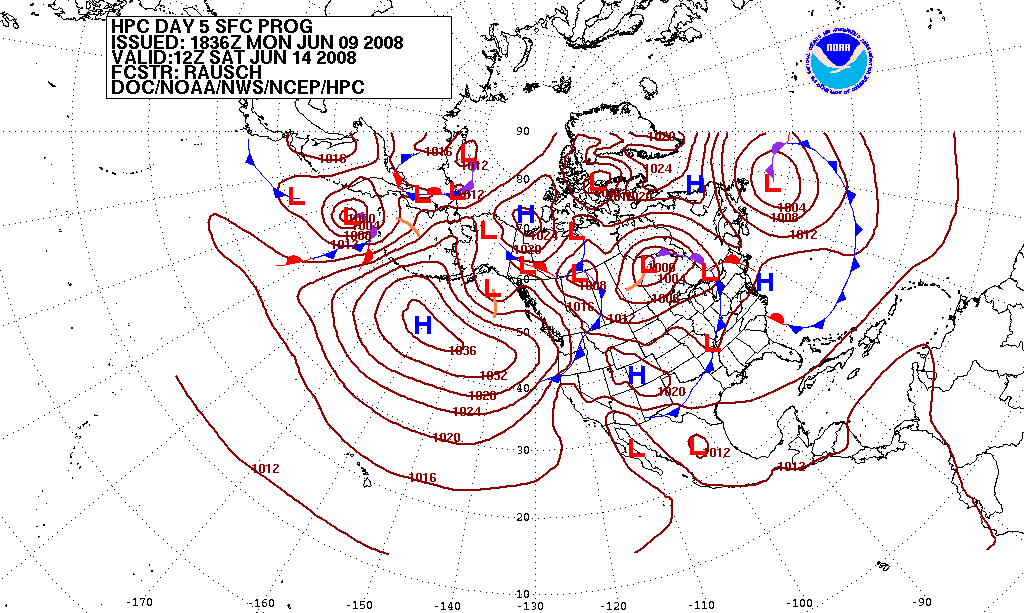
Barnes interpolation, named after Stanley L. Barnes, is the interpolation of unevenly spread data points from a set of measurements of an unknown function in two dimensions into an analytic function of two variables. An example of a situation where the Barnes scheme is important is in weather forecasting where measurements are made wherever monitoring stations may be located, the positions of which are constrained by topography. Such interpolation is essential in data visualisation, e.g. in the construction of contour plots or other representations of analytic surfaces. Introduction Barnes proposed an objective scheme for the interpolation of two dimensional data using a multi-pass scheme. This provided a method to interpolating sea-level pressures across the entire United States of America, producing a synoptic chart across the country using dispersed monitoring stations. Researchers have subsequently improved the Barnes method to reduce the number of parameters required for cal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interpolation
In the mathematics, mathematical field of numerical analysis, interpolation is a type of estimation, a method of constructing (finding) new data points based on the range of a discrete set of known data points. In engineering and science, one often has a number of data points, obtained by sampling (statistics), sampling or experimentation, which represent the values of a function for a limited number of values of the Dependent and independent variables, independent variable. It is often required to interpolate; that is, estimate the value of that function for an intermediate value of the independent variable. A closely related problem is the function approximation, approximation of a complicated function by a simple function. Suppose the formula for some given function is known, but too complicated to evaluate efficiently. A few data points from the original function can be interpolated to produce a simpler function which is still fairly close to the original. The resulting gai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analytic Function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions. Functions of each type are infinitely differentiable, but complex analytic functions exhibit properties that do not generally hold for real analytic functions. A function is analytic if and only if for every x_0 in its domain, its Taylor series about x_0 converges to the function in some neighborhood of x_0 . This is stronger than merely being infinitely differentiable at x_0 , and therefore having a well-defined Taylor series; the Fabius function provides an example of a function that is infinitely differentiable but not analytic. Definitions Formally, a function f is ''real analytic'' on an open set D in the real line if for any x_0\in D one can write f(x) = \sum_^\infty a_ \left( x-x_0 \right)^ = a_0 + a_1 (x-x_0) + a_2 (x-x_0)^2 + \cdots in which the coefficients a_0, a_1, \dots a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weather Forecasting
Weather forecasting or weather prediction is the application of science and technology forecasting, to predict the conditions of the Earth's atmosphere, atmosphere for a given location and time. People have attempted to predict the weather informally for thousands of years and formally since the 19th century. Weather forecasts are made by collecting quantitative data about the current state of the atmosphere, land, and ocean and using meteorology to project how the atmosphere will change at a given place. Once calculated manually based mainly upon changes in atmospheric pressure, barometric pressure, current weather conditions, and sky conditions or cloud cover, weather forecasting now relies on numerical weather prediction, computer-based models that take many atmospheric factors into account. Human input is still required to pick the best possible model to base the forecast upon, which involves pattern recognition skills, teleconnections, knowledge of model performance, and kn ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topography
Topography is the study of the forms and features of land surfaces. The topography of an area may refer to the landforms and features themselves, or a description or depiction in maps. Topography is a field of geoscience and planetary science and is concerned with local detail in general, including not only relief, but also natural, artificial, and cultural features such as roads, land boundaries, and buildings. In the United States, topography often means specifically relief, even though the USGS topographic maps record not just elevation contours, but also roads, populated places, structures, land boundaries, and so on. Topography in a narrow sense involves the recording of relief or terrain, the three-dimensional quality of the surface, and the identification of specific landforms; this is also known as geomorphometry. In modern usage, this involves generation of elevation data in digital form ( DEM). It is often considered to include the graphic representation of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Contour Plot
A contour line (also isoline, isopleth, isoquant or isarithm) of a function of two variables is a curve along which the function has a constant value, so that the curve joins points of equal value. It is a plane section of the three-dimensional graph of the function f(x,y) parallel to the (x,y)-plane. More generally, a contour line for a function of two variables is a curve connecting points where the function has the same particular value. In cartography, a contour line (often just called a "contour") joins points of equal elevation (height) above a given level, such as mean sea level. A contour map is a map illustrated with contour lines, for example a topographic map, which thus shows valleys and hills, and the steepness or gentleness of slopes. The contour interval of a contour map is the difference in elevation between successive contour lines. The gradient of the function is always perpendicular to the contour lines. When the lines are close together the magnitude of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Synoptic Chart
In meteorology, the synoptic scale (also called the large scale or cyclonic scale) is a horizontal length scale of the order of or more. This corresponds to a horizontal scale typical of mid-latitude depressions (e.g. extratropical cyclones). Most high- and low-pressure areas seen on weather maps (such as surface weather analyses) are synoptic-scale systems, driven by the location of Rossby waves in their respective hemisphere. Low-pressure areas and their related frontal zones occur on the leading edge of a trough within the Rossby wave pattern, while high-pressure areas form on the back edge of the trough. Most precipitation areas occur near frontal zones. The word '' synoptic'' is derived from the Ancient Greek word (), meaning "seen together". The Navier–Stokes equations applied to atmospheric motion can be simplified by scale analysis in the synoptic scale. It can be shown that the main terms in horizontal equations are Coriolis force and pressure gradient terms; t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian Function
In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function (mathematics), function of the base form f(x) = \exp (-x^2) and with parametric extension f(x) = a \exp\left( -\frac \right) for arbitrary real number, real constants , and non-zero . It is named after the mathematician Carl Friedrich Gauss. The graph of a function, graph of a Gaussian is a characteristic symmetric "Normal distribution, bell curve" shape. The parameter is the height of the curve's peak, is the position of the center of the peak, and (the standard deviation, sometimes called the Gaussian Root mean square, RMS width) controls the width of the "bell". Gaussian functions are often used to represent the probability density function of a normal distribution, normally distributed random variable with expected value and variance . In this case, the Gaussian is of the form g(x) = \frac \exp\left( -\frac \frac \right). Gaussian functions are widely used in statistics to describ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complete Spatial Randomness
Complete spatial randomness (CSR) describes a point process whereby point events occur within a given study area in a completely random fashion. It is synonymous with a ''homogeneous spatial Poisson process''.O. Maimon, L. Rokach, ''Data Mining and Knowledge Discovery Handbook'', Second Edition, Springer 2010, pages 851-852 Such a process is modeled using only one parameter \rho, i.e. the density of points within the defined area. The term complete spatial randomness is commonly used in Applied Statistics in the context of examining certain point patterns, whereas in most other statistical contexts it is referred to the concept of a spatial Poisson process. Model Data in the form of a set of points, irregularly distributed within a region of space, arise in many different contexts; examples include locations of trees in a forest, of nests of birds, of nuclei in tissue, of ill people in a population at risk. We call any such data-set a spatial point pattern and refer to the loc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cluster Analysis
Cluster analysis or clustering is the data analyzing technique in which task of grouping a set of objects in such a way that objects in the same group (called a cluster) are more Similarity measure, similar (in some specific sense defined by the analyst) to each other than to those in other groups (clusters). It is a main task of exploratory data analysis, and a common technique for statistics, statistical data analysis, used in many fields, including pattern recognition, image analysis, information retrieval, bioinformatics, data compression, computer graphics and machine learning. Cluster analysis refers to a family of algorithms and tasks rather than one specific algorithm. It can be achieved by various algorithms that differ significantly in their understanding of what constitutes a cluster and how to efficiently find them. Popular notions of clusters include groups with small Distance function, distances between cluster members, dense areas of the data space, intervals or pa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interpolation
In the mathematics, mathematical field of numerical analysis, interpolation is a type of estimation, a method of constructing (finding) new data points based on the range of a discrete set of known data points. In engineering and science, one often has a number of data points, obtained by sampling (statistics), sampling or experimentation, which represent the values of a function for a limited number of values of the Dependent and independent variables, independent variable. It is often required to interpolate; that is, estimate the value of that function for an intermediate value of the independent variable. A closely related problem is the function approximation, approximation of a complicated function by a simple function. Suppose the formula for some given function is known, but too complicated to evaluate efficiently. A few data points from the original function can be interpolated to produce a simpler function which is still fairly close to the original. The resulting gai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |