|
Axis–angle Representation
In mathematics, the axis–angle representation parameterizes a rotation in a three-dimensional Euclidean space by two quantities: a unit vector indicating the direction of an axis of rotation, and an angle of rotation describing the magnitude and sense (e.g., clockwise) of the rotation about the axis. Only two numbers, not three, are needed to define the direction of a unit vector rooted at the origin because the magnitude of is constrained. For example, the elevation and azimuth angles of suffice to locate it in any particular Cartesian coordinate frame. By Rodrigues' rotation formula, the angle and axis determine a transformation that rotates three-dimensional vectors. The rotation occurs in the sense prescribed by the right-hand rule. The rotation axis is sometimes called the Euler axis. The axis–angle representation is predicated on Euler's rotation theorem, which dictates that any rotation or sequence of rotations of a rigid body in a three-dimensional space ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angle Axis Vector
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight lines at a point. Formally, an angle is a figure lying in a plane formed by two rays, called the '' sides'' of the angle, sharing a common endpoint, called the '' vertex'' of the angle. More generally angles are also formed wherever two lines, rays or line segments come together, such as at the corners of triangles and other polygons. An angle can be considered as the region of the plane bounded by the sides. Angles can also be formed by the intersection of two planes or by two intersecting curves, in which case the rays lying tangent to each curve at the point of intersection define the angle. The term ''angle'' is also used for the size, magnitude or quantity of these types of geometric figures and in this context an angle consists of a number and unit of measurement. Angular measure or measure of angle are sometimes used to distinguish between the measurement and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix Exponential
In mathematics, the matrix exponential is a matrix function on square matrix, square matrices analogous to the ordinary exponential function. It is used to solve systems of linear differential equations. In the theory of Lie groups, the matrix exponential gives the exponential map (Lie theory), exponential map between a matrix Lie algebra and the corresponding Lie group. Let be an real number, real or complex number, complex matrix (mathematics), matrix. The exponential of , denoted by or , is the matrix given by the power series e^X = \sum_^\infty \frac X^k where X^0 is defined to be the identity matrix I with the same dimensions as X, and . The series always converges, so the exponential of is well-defined. Equivalently, e^X = \lim_ \left(I + \frac \right)^k for integer-valued , where is the identity matrix. Equivalently, given by the solution to the differential equation \frac d e^ = X e^, \quad e^ = I When is an diagonal matrix then will be an diagonal matr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Map (Lie Theory)
In the theory of Lie groups, the exponential map is a map from the Lie algebra \mathfrak g of a Lie group G to the group, which allows one to recapture the local group structure from the Lie algebra. The existence of the exponential map is one of the primary reasons that Lie algebras are a useful tool for studying Lie groups. The ordinary exponential function of mathematical analysis is a special case of the exponential map when G is the multiplicative group of positive real numbers (whose Lie algebra is the additive group of all real numbers). The exponential map of a Lie group satisfies many properties analogous to those of the ordinary exponential function, however, it also differs in many important respects. Definitions Let G be a Lie group and \mathfrak g be its Lie algebra (thought of as the tangent space to the identity element of G). The exponential map is a map :\exp\colon \mathfrak g \to G which can be defined in several different ways. The typical modern definition ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Olinde Rodrigues
Benjamin Olinde Rodrigues (6 October 1795 – 17 December 1851), more commonly known as Olinde Rodrigues, was a French banker, mathematician, and social reformer. In mathematics Rodrigues is remembered for Rodrigues' rotation formula for vectors, the Rodrigues formula for the Legendre polynomials, and the Euler–Rodrigues parameters. Biography Rodrigues was born into a well-to-do Sephardi Jewish family in Bordeaux. His family was of Portuguese-Jewish descent. He was awarded a doctorate in mathematics on 28 June 1815 by the University of Paris. His dissertation contains the result now called Rodrigues' formula. After graduation, Rodrigues became a banker. A close associate of the Comte de Saint-Simon, Rodrigues continued, after Saint-Simon's death in 1825, to champion the older man's socialist ideals, a school of thought that came to be known as Saint-Simonianism. During this period, Rodrigues published writings on politics, social reform, and banking. Rodrigues' 1840 pa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mercer's Theorem
In mathematics, specifically functional analysis, Mercer's theorem is a representation of a symmetric positive-definite function on a square as a sum of a convergent sequence of product functions. This theorem, presented in , is one of the most notable results of the work of James Mercer (1883–1932). It is an important theoretical tool in the theory of integral equations; it is used in the Hilbert space theory of stochastic processes, for example the Karhunen–Loève theorem; and it is also used in the reproducing kernel Hilbert space theory where it characterizes a symmetric positive-definite kernel as a reproducing kernel. Introduction To explain Mercer's theorem, we first consider an important special case; see below for a more general formulation. A ''kernel'', in this context, is a symmetric continuous function : K: ,b\times ,b\rightarrow \mathbb where K(x,y) = K(y,x) for all x,y \in ,b/math>. ''K'' is said to be a positive-definite kernel if and only if ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time
Time is the continuous progression of existence that occurs in an apparently irreversible process, irreversible succession from the past, through the present, and into the future. It is a component quantity of various measurements used to sequence events, to compare the duration of events (or the intervals between them), and to quantify rates of change of quantities in material reality or in the qualia, conscious experience. Time is often referred to as a fourth dimension, along with Three-dimensional space, three spatial dimensions. Time is one of the seven fundamental physical quantities in both the International System of Units (SI) and International System of Quantities. The SI base unit of time is the second, which is defined by measuring the electronic transition frequency of caesium atoms. General relativity is the primary framework for understanding how spacetime works. Through advances in both theoretical and experimental investigations of spacetime, it has been shown ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Function
In mathematics, a continuous function is a function such that a small variation of the argument induces a small variation of the value of the function. This implies there are no abrupt changes in value, known as '' discontinuities''. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is . Until the 19th century, mathematicians largely relied on intuitive notions of continuity and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity. Continuity is one of the core concepts of calculus and mathematical analysis, where arguments and values of functions are real and complex numbers. The concept has been generalized to functions between metric spaces and between topological spaces. The latter are the most general continuous functions, and their d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constant Function
In mathematics, a constant function is a function whose (output) value is the same for every input value. Basic properties As a real-valued function of a real-valued argument, a constant function has the general form or just For example, the function is the specific constant function where the output value is . The domain of this function is the set of all real numbers. The image of this function is the singleton set . The independent variable does not appear on the right side of the function expression and so its value is "vacuously substituted"; namely , , , and so on. No matter what value of is input, the output is . The graph of the constant function is a ''horizontal line'' in the plane that passes through the point . In the context of a polynomial in one variable , the constant function is called ''non-zero constant function'' because it is a polynomial of degree 0, and its general form is , where is nonzero. This function has no intersection point with the a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
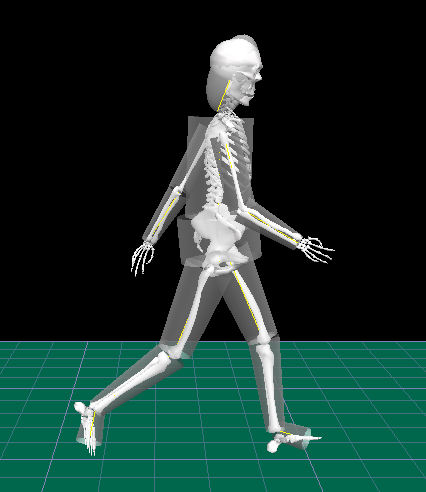
Rigid Body
In physics, a rigid body, also known as a rigid object, is a solid body in which deformation is zero or negligible, when a deforming pressure or deforming force is applied on it. The distance between any two given points on a rigid body remains constant in time regardless of external forces or moments exerted on it. A rigid body is usually considered as a continuous distribution of mass. Mechanics of rigid bodies is a field within mechanics where motions and forces of objects are studied without considering effects that can cause deformation (as opposed to mechanics of materials, where deformable objects are considered). In the study of special relativity, a perfectly rigid body does not exist; and objects can only be assumed to be rigid if they are not moving near the speed of light, where the mass is infinitely large. In quantum mechanics, a rigid body is usually thought of as a collection of point masses. For instance, molecules (consisting of the point masses: electr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Motion (physics)
In physics, motion is when an object changes its position with respect to a reference point in a given time. Motion is mathematically described in terms of displacement, distance, velocity, acceleration, speed, and frame of reference to an observer, measuring the change in position of the body relative to that frame with a change in time. The branch of physics describing the motion of objects without reference to their cause is called ''kinematics'', while the branch studying forces and their effect on motion is called '' dynamics''. If an object is not in motion relative to a given frame of reference, it is said to be ''at rest'', ''motionless'', ''immobile'', '' stationary'', or to have a constant or time-invariant position with reference to its surroundings. Modern physics holds that, as there is no absolute frame of reference, Isaac Newton's concept of '' absolute motion'' cannot be determined. Everything in the universe can be considered to be in motion. Motion applies to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rotation
Rotation or rotational/rotary motion is the circular movement of an object around a central line, known as an ''axis of rotation''. A plane figure can rotate in either a clockwise or counterclockwise sense around a perpendicular axis intersecting anywhere inside or outside the figure at a ''center of rotation''. A solid figure has an infinite number of possible axes and angles of rotation, including chaotic rotation (between arbitrary orientation (geometry), orientations), in contrast to rotation around a fixed axis, rotation around a axis. The special case of a rotation with an internal axis passing through the body's own center of mass is known as a spin (or ''autorotation''). In that case, the surface intersection of the internal ''spin axis'' can be called a ''pole''; for example, Earth's rotation defines the geographical poles. A rotation around an axis completely external to the moving body is called a revolution (or ''orbit''), e.g. Earth's orbit around the Sun. The en ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rigid-body Dynamics
In the physical science of dynamics, rigid-body dynamics studies the movement of systems of interconnected bodies under the action of external forces. The assumption that the bodies are '' rigid'' (i.e. they do not deform under the action of applied forces) simplifies analysis, by reducing the parameters that describe the configuration of the system to the translation and rotation of reference frames attached to each body. This excludes bodies that display fluid, highly elastic, and plastic behavior. The dynamics of a rigid body system is described by the laws of kinematics and by the application of Newton's second law ( kinetics) or their derivative form, Lagrangian mechanics. The solution of these equations of motion provides a description of the position, the motion and the acceleration of the individual components of the system, and overall the system itself, as a function of time. The formulation and solution of rigid body dynamics is an important tool in the compute ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |