|
Archimedes's Use Of Infinitesimals
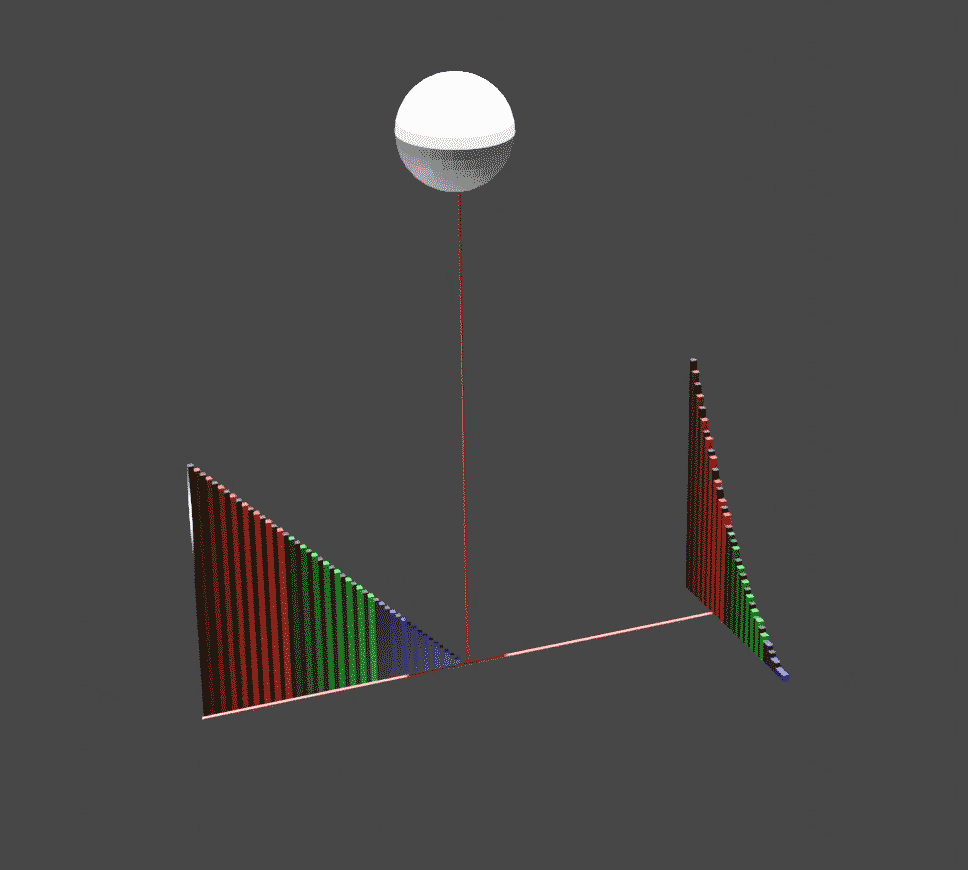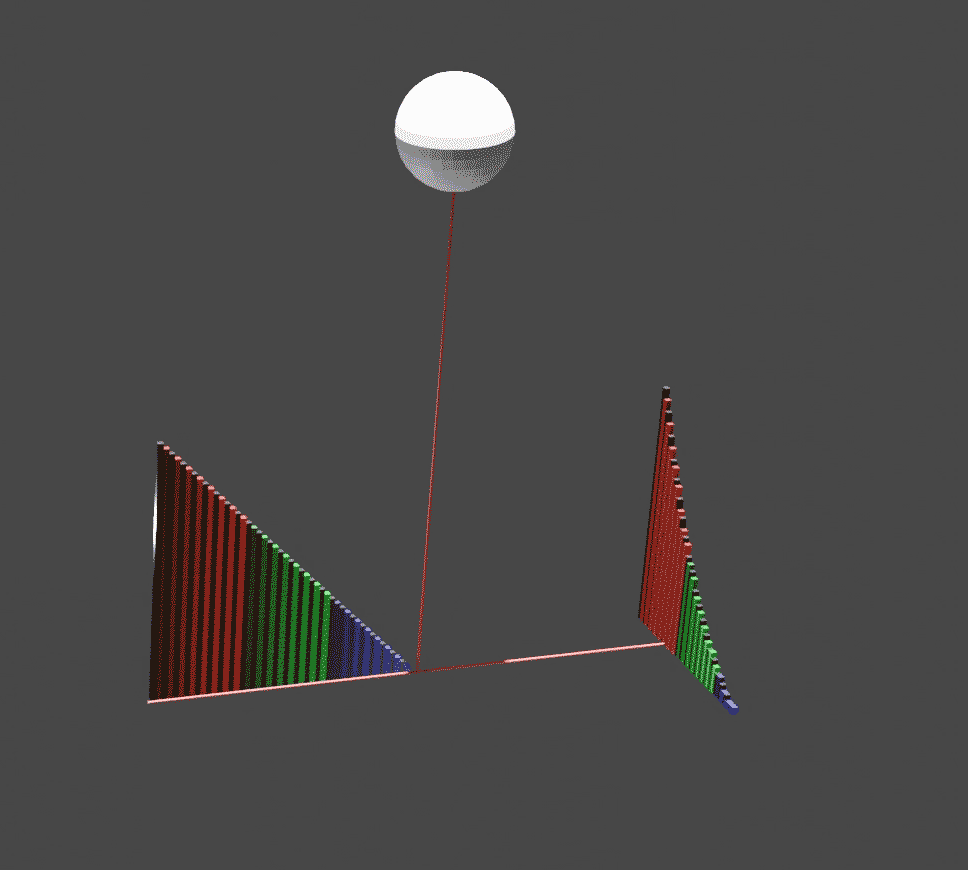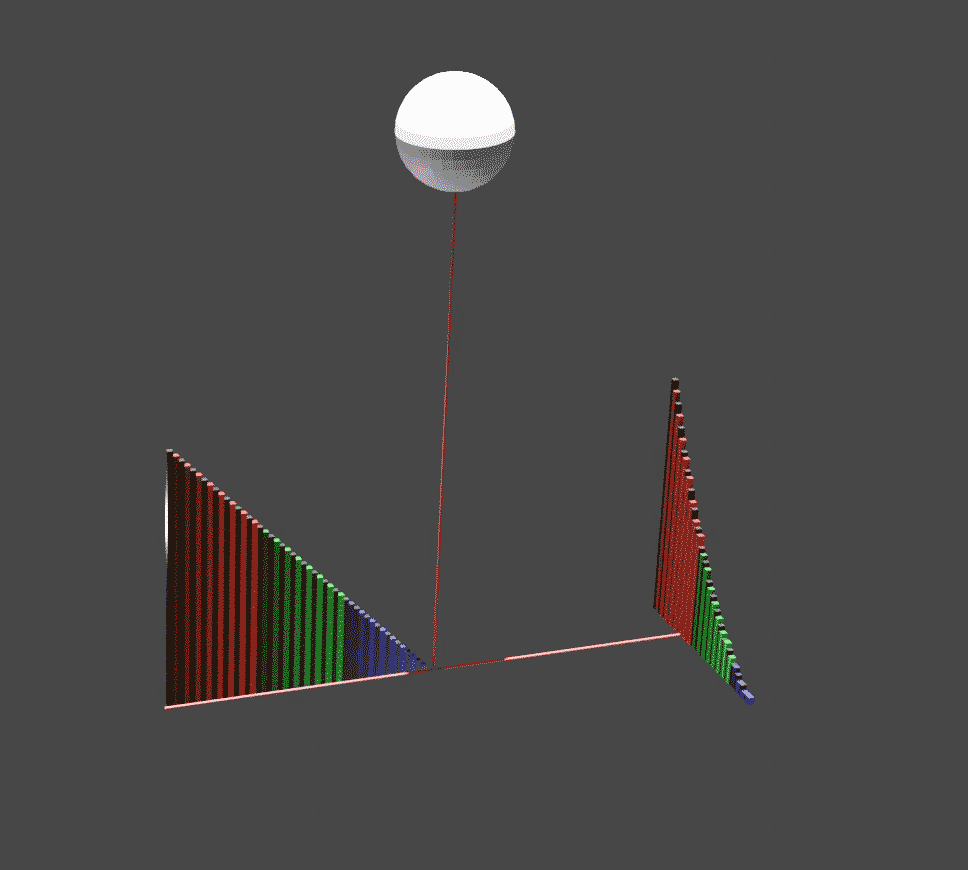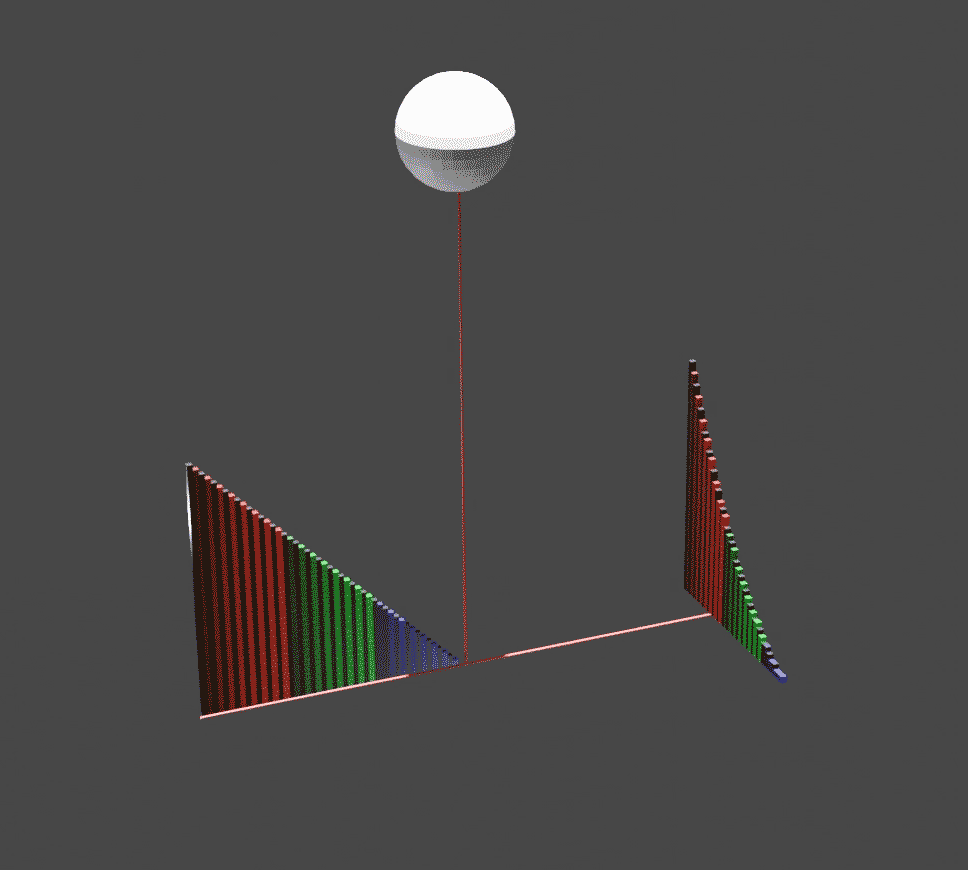
''The Method of Mechanical Theorems'' (), also referred to as ''The Method'', is one of the major surviving works of the ancient Greek polymath Archimedes. ''The Method'' takes the form of a letter from Archimedes to Eratosthenes, the chief librarian at the Library of Alexandria, and contains the first attested explicit use of indivisibles (indivisibles are geometric versions of infinitesimals). The work was originally thought to be lost, but in 1906 was rediscovered in the celebrated Archimedes Palimpsest. The palimpsest includes Archimedes' account of the "mechanical method", so called because it relies on the center of weights of figures (centroid) and the law of the lever, which were demonstrated by Archimedes in ''On the Equilibrium of Planes''. Archimedes did not admit the method of indivisibles as part of rigorous mathematics, and therefore did not publish his method in the formal treatises that contain the results. In these treatises, he proves the same theorems by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ancient Greece
Ancient Greece () was a northeastern Mediterranean civilization, existing from the Greek Dark Ages of the 12th–9th centuries BC to the end of classical antiquity (), that comprised a loose collection of culturally and linguistically related city-states and communities. Prior to the Roman period, most of these regions were officially unified only once under the Kingdom of Macedon from 338 to 323 BC. In Western history, the era of classical antiquity was immediately followed by the Early Middle Ages and the Byzantine period. Three centuries after the decline of Mycenaean Greece during the Bronze Age collapse, Greek urban poleis began to form in the 8th century BC, ushering in the Archaic period and the colonization of the Mediterranean Basin. This was followed by the age of Classical Greece, from the Greco-Persian Wars to the death of Alexander the Great in 323 BC, and which included the Golden Age of Athens and the Peloponnesian War. The u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parabola
In mathematics, a parabola is a plane curve which is Reflection symmetry, mirror-symmetrical and is approximately U-shaped. It fits several superficially different Mathematics, mathematical descriptions, which can all be proved to define exactly the same curves. One description of a parabola involves a Point (geometry), point (the Focus (geometry), focus) and a Line (geometry), line (the Directrix (conic section), directrix). The focus does not lie on the directrix. The parabola is the locus (mathematics), locus of points in that plane that are equidistant from the directrix and the focus. Another description of a parabola is as a conic section, created from the intersection of a right circular conical surface and a plane (geometry), plane Parallel (geometry), parallel to another plane that is tangential to the conical surface. The graph of a function, graph of a quadratic function y=ax^2+bx+ c (with a\neq 0 ) is a parabola with its axis parallel to the -axis. Conversely, every ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thomas Little Heath
Sir Thomas Little Heath (; 5 October 1861 – 16 March 1940) was a British civil servant, mathematician, classics, classical scholar, historian of ancient Greek mathematics, translator, and Mountaineering, mountaineer. He was educated at Clifton College. Heath translated works of Euclid of Alexandria, Apollonius of Perga, Aristarchus of Samos, and Archimedes of Syracuse, Italy, Syracuse into English. Life Heath was born in Barnetby-le-Wold, Lincolnshire, England, being the third son of a farmer, Samuel Heath, and his wife Mary Little. He had two brothers and three sisters. He was educated at Caistor Grammar School and Clifton College before entering Trinity College, Cambridge, where he was awarded an ScD in 1896 and became an Honorary Fellow in 1920. He got first class honours in both the classical tripos and mathematical tripos and was the twelfth Wrangler (University of Cambridge), wrangler in 1882. In 1884 he took the Civil Service examination and became an Assistant Secretar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cambridge University Press
Cambridge University Press was the university press of the University of Cambridge. Granted a letters patent by King Henry VIII in 1534, it was the oldest university press in the world. Cambridge University Press merged with Cambridge Assessment to form Cambridge University Press and Assessment under Queen Elizabeth II's approval in August 2021. With a global sales presence, publishing hubs, and offices in more than 40 countries, it published over 50,000 titles by authors from over 100 countries. Its publications include more than 420 academic journals, monographs, reference works, school and university textbooks, and English language teaching and learning publications. It also published Bibles, runs a bookshop in Cambridge, sells through Amazon, and has a conference venues business in Cambridge at the Pitt Building and the Sir Geoffrey Cass Sports and Social Centre. It also served as the King's Printer. Cambridge University Press, as part of the University of Cambridge, was a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hemisphere
Hemisphere may refer to: In geometry * Hemisphere (geometry), a half of a sphere As half of Earth or any spherical astronomical object * A hemisphere of Earth ** Northern Hemisphere ** Southern Hemisphere ** Eastern Hemisphere ** Western Hemisphere ** Land and water hemispheres * A half of the (geocentric) celestial sphere ** Northern celestial hemisphere ** Southern celestial hemisphere * A cultural hemisphere * The near or far side of the Moon As half of the brain * A cerebral hemisphere, a division of the cerebrum * A half of the cerebellum, a smaller part of the brain Other * ''Hémisphère'' (Paradis), a 12-inch album by French artists Paradis * ''Hemispheres'' (magazine), an inflight publication * ''Hemispheres'' (TV series), Canadian and Australian news program * ''Hemispheres'' (Rush album), 1978 * ''Hemispheres'' (Lily Afshar album), 2006 * ''Hemispheres'' (Doseone album), 1998 * L'Hemisfèric at the Ciutat de les Arts i les Ciències, Valencia, Spain * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Area
The surface area (symbol ''A'') of a solid object is a measure of the total area that the surface of the object occupies. The mathematical definition of surface area in the presence of curved surfaces is considerably more involved than the definition of arc length of one-dimensional curves, or of the surface area for polyhedra (i.e., objects with flat polygonal faces), for which the surface area is the sum of the areas of its faces. Smooth surfaces, such as a sphere, are assigned surface area using their representation as parametric surfaces. This definition of surface area is based on methods of infinitesimal calculus and involves partial derivatives and double integration. A general definition of surface area was sought by Henri Lebesgue and Hermann Minkowski at the turn of the twentieth century. Their work led to the development of geometric measure theory, which studies various notions of surface area for irregular objects of any dimension. An important example is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jan Hogendijk
Jan Pieter Hogendijk (born 21 July 1955) is a Dutch mathematician and historian of science. Since 2005, he is professor of history of mathematics at the University of Utrecht. Hogendijk became a member of the Royal Netherlands Academy of Arts and Sciences in 2010. Hogendijk has contributed to the study of Greek mathematics and mathematics in medieval Islam; he provides a list of Sources on his website (below). In 2012, he was awarded the inaugural Otto Neugebauer Prize for History of Mathematics, by the European Mathematical Society, "for having illuminated how Greek mathematics was absorbed in the medieval Arabic world, how mathematics developed in medieval Islam, and how it was eventually transmitted to Europe." A bibliography Bibliography (from and ), as a discipline, is traditionally the academic study of books as physical, cultural objects; in this sense, it is also known as bibliology (from ). English author and bibliographer John Carter describes ''bibliograph ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bicylinder
In geometry, a Steinmetz solid is the Solid geometry, solid body obtained as the intersection of two or three cylinders of equal radius Perpendicular, at right angles. Each of the curves of the intersection of two cylinders is an ellipse. The intersection of two cylinders is called a bicylinder. Topologically, it is equivalent to a square hosohedron. The intersection of three cylinders is called a tricylinder. A Bisection, bisected bicylinder is called a vault, and a cloister vault in architecture has this shape. Steinmetz solids are named after mathematician Charles Proteus Steinmetz, who solved the problem of determining the volume of the intersection. However, the same problem had been solved earlier, by Archimedes in the ancient Greek world, Zu Chongzhi in ancient China, and Piero della Francesca in the early Italian Renaissance. They appear prominently in the sculptures of Frank Smullin. Bicylinder A bicylinder generated by two cylinders with radius has the volume V ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
On The Sphere And Cylinder
''On the Sphere and Cylinder'' () is a treatise that was published by Archimedes in two volumes . It most notably details how to find the surface area of a sphere and the volume of the contained ball and the analogous values for a cylinder, and was the first to do so. Contents The principal formulae derived in ''On the Sphere and Cylinder'' are those mentioned above: the surface area of the sphere, the volume of the contained ball, and surface area and volume of the cylinder. Let r be the radius of the sphere and cylinder, and h be the height of the cylinder, with the assumption that the cylinder is a right cylinder—the side is perpendicular to both caps. In his work, Archimedes showed that the surface area of a cylinder is equal to: :A_C = 2 \pi r^2 + 2 \pi r h = 2 \pi r ( r + h ).\, and that the volume of the same is: :V_C = \pi r^2 h. \, On the sphere, he showed that the surface area is four times the area of its great circle. In modern terms, this means that the surf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Measurement Of The Circle
''Measurement of a Circle'' or ''Dimension of the Circle'' (Greek: , ''Kuklou metrēsis'') is a treatise that consists of three propositions, probably made by Archimedes, ca. 250 BCE. The treatise is only a fraction of what was a longer work. Propositions Proposition one Proposition one states: The area of any circle is equal to a right-angled triangle in which one of the sides about the right angle is equal to the radius, and the other to the circumference of the circle. Any circle with a circumference ''c'' and a radius ''r'' is equal in area with a right triangle with the two legs being ''c'' and ''r''. This proposition is proved by the method of exhaustion. Proposition two Proposition two states: The area of a circle is to the square on its diameter as 11 to 14. This proposition could not have been placed by Archimedes, for it relies on the outcome of the third proposition. Proposition three Proposition three states: The ratio of the circumference of any circle to its di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spheroids
A spheroid, also known as an ellipsoid of revolution or rotational ellipsoid, is a quadric surface (mathematics), surface obtained by Surface of revolution, rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters. A spheroid has circular symmetry. If the ellipse is rotated about its major axis, the result is a ''prolate spheroid'', elongated like a rugby ball. The ball (gridiron football), American football is similar but has a pointier end than a spheroid could. If the ellipse is rotated about its minor axis, the result is an ''oblate spheroid'', flattened like a lentil or a plain M&M's, M&M. If the generating ellipse is a circle, the result is a sphere. Due to the combined effects of gravity and rotation of the Earth, rotation, the figure of the Earth (and of all planets) is not quite a sphere, but instead is slightly flattening, flattened in the direction of its axis of rotation. For that reason, in cartography and geode ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volume Of A Sphere
A sphere (from Greek , ) is a surface analogous to the circle, a curve. In solid geometry, a sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the ''center'' of the sphere, and the distance is the sphere's ''radius''. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians. The sphere is a fundamental surface in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres roll smoothly in any direction, so most balls used in sports and toys are spherical, as are ball bearings. Basic terminology As mentioned earlier ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |