 |
Archimedean Graph
In the mathematics, mathematical field of graph theory, an Archimedean graph is a Graph (discrete mathematics), graph that forms the skeleton of one of the Archimedean solids. There are 13 Archimedean graphs, and all of them are regular graph, regular, polyhedral graph, polyhedral (and therefore by necessity also K-vertex-connected graph, 3-vertex-connected planar graphs), and also Hamiltonian graphs. Along with the 13, the infinite sets of prism graphs and antiprism graphs can also be considered Archimedean graphs.An Atlas of Graphs, p. 261 See also *Platonic graph *Wheel graph References * Read, R. C. and Wilson, R. J. ''An Atlas of Graphs'', Oxford, England: Oxford University Press, 2004 reprint, Chapter 6 ''special graphs'' pp. 261, 267–269. External links * Regular graphs Planar graphs {{graph-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
 |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Cubic Graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words, a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs. A bicubic graph is a cubic bipartite graph. Symmetry In 1932, Ronald M. Foster began collecting examples of cubic symmetric graphs, forming the start of the Foster census.. Many well-known individual graphs are cubic and symmetric, including the utility graph, the Petersen graph, the Heawood graph, the Möbius–Kantor graph, the Pappus graph, the Desargues graph, the Nauru graph, the Coxeter graph, the Tutte–Coxeter graph, the Dyck graph, the Foster graph and the Biggs–Smith graph. W. T. Tutte classified the symmetric cubic graphs by the smallest integer number ''s'' such that each two oriented paths of length ''s'' can be mapped to each other by exactly one symmetry of the graph. He showed that ''s'' is at most 5, and provided examples of graphs with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Truncated Icosahedral Graph
In geometry, the truncated icosahedron is a polyhedron that can be constructed by truncating all of the regular icosahedron's vertices. Intuitively, it may be regarded as footballs (or soccer balls) that are typically patterned with white hexagons and black pentagons. It can be found in the application of geodesic dome structures such as those whose architecture Buckminster Fuller pioneered are often based on this structure. It is an example of an Archimedean solid, as well as a Goldberg polyhedron. Construction The truncated icosahedron can be constructed from a regular icosahedron by cutting off all of its vertices, known as truncation. Each of the 12 vertices at the one-third mark of each edge creates 12 pentagonal faces and transforms the original 20 triangle faces into regular hexagons. Therefore, the resulting polyhedron has 32 faces, 90 edges, and 60 vertices. A Goldberg polyhedron is one whose faces are 12 pentagons and some multiple of 10 hexagons. There are three ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Truncated Dodecahedral Graph
In mathematics and computer science, truncation is limiting the number of digits right of the decimal point. Truncation and floor function Truncation of positive real numbers can be done using the floor function. Given a number x \in \mathbb_+ to be truncated and n \in \mathbb_0, the number of elements to be kept behind the decimal point, the truncated value of x is :\operatorname(x,n) = \frac. However, for negative numbers truncation does not round in the same direction as the floor function: truncation always rounds toward zero, the \operatorname function rounds towards negative infinity. For a given number x \in \mathbb_-, the function \operatorname is used instead :\operatorname(x,n) = \frac. Causes of truncation With computers, truncation can occur when a decimal number is typecast as an integer; it is truncated to zero decimal digits because integers cannot store non-integer real numbers. In algebra An analogue of truncation can be applied to polynomials. In t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Icosidodecahedral Graph
In geometry, an icosidodecahedron or pentagonal gyrobirotunda is a polyhedron with twenty (''icosi-'') triangular faces and twelve (''dodeca-'') pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon. As such, it is one of the Archimedean solids and more particularly, a quasiregular polyhedron. Construction One way to construct the icosidodecahedron is to start with two pentagonal rotunda by attaching them to their bases. These rotundas cover their decagonal base so that the resulting polyhedron has 32 faces, 30 vertices, and 60 edges. This construction is similar to one of the Johnson solids, the pentagonal orthobirotunda. The difference is that the icosidodecahedron is constructed by twisting its rotundas by 36°, a process known as gyration, resulting in the pentagonal face connecting to the triangular one. The icosidodecahedron has an alternat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Quintic Graph
In mathematics, a quintic function is a function of the form :g(x)=ax^5+bx^4+cx^3+dx^2+ex+f,\, where , , , , and are members of a field, typically the rational numbers, the real numbers or the complex numbers, and is nonzero. In other words, a quintic function is defined by a polynomial of degree five. Because they have an odd degree, normal quintic functions appear similar to normal cubic functions when graphed, except they may possess one additional local maximum and one additional local minimum. The derivative of a quintic function is a quartic function. Setting and assuming produces a quintic equation of the form: :ax^5+bx^4+cx^3+dx^2+ex+f=0.\, Solving quintic equations in terms of radicals (''n''th roots) was a major problem in algebra from the 16th century, when cubic and quartic equations were solved, until the first half of the 19th century, when the impossibility of such a general solution was proved with the Abel–Ruffini theorem. Finding roots of a quintic e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Snub Cubic Graph
A snub, cut, or slight is a refusal to recognise an acquaintance by ignoring them, avoiding them or pretending not to know them. For example, a failure to greet someone may be considered a snub. In awards and lists For awards, the term "snub" is usually used to refer to a work or person that fails to be nominated or win award, with whether or not a person or work was legitimately snubbed for an award has often been subject for public debate. The term "snub" has also been used in relation to lists, such as the NBA 75th Anniversary Team. Many notable people and works have failed to be nominated or win a major award. For example, Alfred Hitchcock and Stanley Kubrick never won best director at the Oscars despite being nominated five and four times respectively, and Glenn Close, Peter O'Toole, Deborah Kerr, Sigourney Weaver and Cicely Tyson have never won an Oscar related to acting despite each having multiple nominations. Among films, ''Citizen Kane,'' ''E.T. the Extra-Terrestrial ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
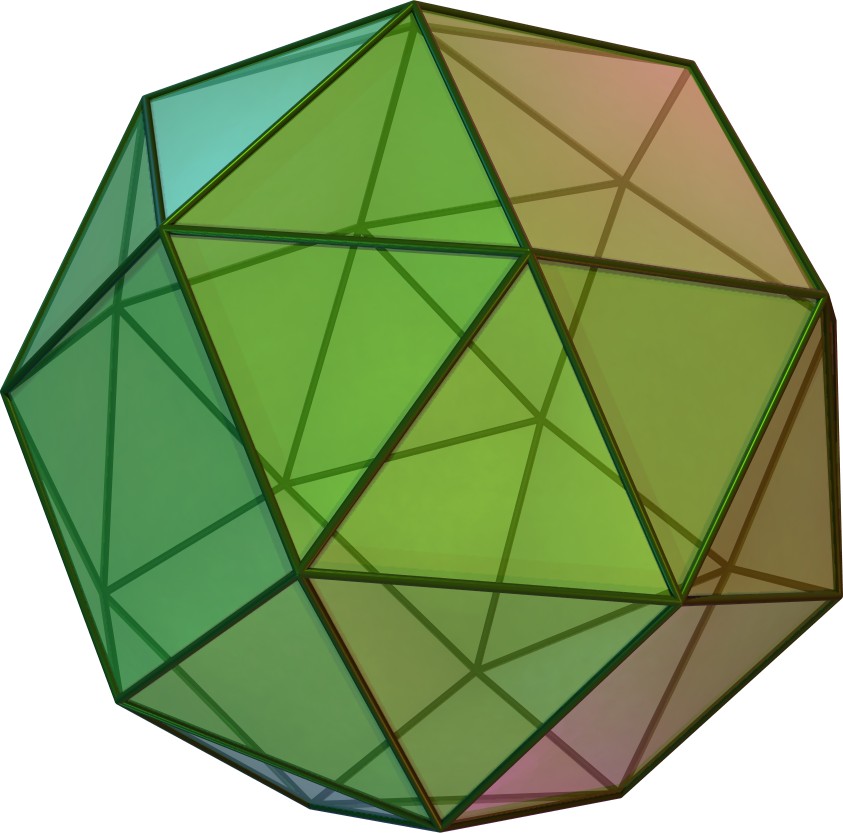 |
Snub Cubical Graph
In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid with 38 faces: 6 squares and 32 equilateral triangles. It has 60 edges and 24 vertices. Kepler first named it in Latin as ''cubus simus'' in 1619 in his Harmonices Mundi. H. S. M. Coxeter, noting it could be derived equally from the octahedron as the cube, called it snub cuboctahedron, with a vertical extended Schläfli symbol s \scriptstyle\begin 4 \\ 3 \end, and representing an alternation of a truncated cuboctahedron, which has Schläfli symbol t \scriptstyle\begin 4 \\ 3 \end. Construction The snub cube can be generated by taking the six faces of the cube, pulling them outward so they no longer touch, then giving them each a small rotation on their centers (all clockwise or all counter-clockwise) until the spaces between can be filled with equilateral triangles. The snub cube may also be constructed from a rhombicuboctahedron. It started by twisting its square face (in blue), allowing its triangl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
 |
Truncated Cuboctahedral Graph
In geometry, the truncated cuboctahedron or great rhombicuboctahedron is an Archimedean solid, named by Kepler as a Truncation (geometry), truncation of a cuboctahedron. It has 12 Square (geometry), square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices, and 72 edges. Since each of its faces has point symmetry (equivalently, 180° rotational symmetry), the truncated cuboctahedron is a 9-zonohedron. The truncated cuboctahedron can Omnitruncated cubic honeycomb, tessellate with the octagonal prism. Names There is a nonconvex uniform polyhedron with a similar name: the nonconvex great rhombicuboctahedron. Cartesian coordinates The Cartesian coordinates for the vertices of a truncated cuboctahedron having edge length 2 and centered at the origin are all the permutations of: \Bigl(\pm 1, \quad \pm\left(1 + \sqrt 2\right), \quad \pm\left(1 + 2\sqrt 2\right) \Bigr). Area and volume The area ''A'' and the volume ''V'' of the truncated cuboctahedron of edge leng ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
 |
Rhombicuboctahedral Graph
In geometry, the rhombicuboctahedron is an Archimedean solid with 26 faces, consisting of 8 equilateral triangles and 18 squares. It was named by Johannes Kepler in his 1618 Harmonices Mundi, being short for ''truncated cuboctahedral rhombus'', with cuboctahedral rhombus being his name for a rhombic dodecahedron. The rhombicuboctahedron is an Archimedean solid, and its dual is a Catalan solid, the deltoidal icositetrahedron. The elongated square gyrobicupola is a polyhedron that is similar to a rhombicuboctahedron, but it is not an Archimedean solid because it is not vertex-transitive. The rhombicuboctahedron is found in diverse cultures in architecture, toys, the arts, and elsewhere. Construction The rhombicuboctahedron may be constructed from a cube by drawing a smaller one in the middle of each face, parallel to the cube's edges. After removing the edges of a cube, the squares may be joined by adding more squares adjacent between them, and the corners may be filled by the e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Truncated Octahedral Graph
In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces (8 regular hexagons and 6 squares), 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a 6-zonohedron. It is also the Goldberg polyhedron GIV(1,1), containing square and hexagonal faces. Like the cube, it can tessellate (or "pack") 3-dimensional space, as a permutohedron. The truncated octahedron was called the "mecon" by Buckminster Fuller. Its dual polyhedron is the tetrakis hexahedron. If the original truncated octahedron has unit edge length, its dual tetrakis hexahedron has edge lengths and . Classifications As an Archimedean solid A truncated octahedron is constructed from a regular octahedron by cutting off all vertices. This resulting polyhedron has six squares and eight hexagons, leaving out six square pyramids. Set ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Truncated Cubic Graph
In mathematics and computer science, truncation is limiting the number of digits right of the decimal point. Truncation and floor function Truncation of positive real numbers can be done using the floor function. Given a number x \in \mathbb_+ to be truncated and n \in \mathbb_0, the number of elements to be kept behind the decimal point, the truncated value of x is :\operatorname(x,n) = \frac. However, for negative numbers truncation does not round in the same direction as the floor function: truncation always rounds toward zero, the \operatorname function rounds towards negative infinity. For a given number x \in \mathbb_-, the function \operatorname is used instead :\operatorname(x,n) = \frac. Causes of truncation With computers, truncation can occur when a decimal number is typecast as an integer; it is truncated to zero decimal digits because integers cannot store non-integer real numbers. In algebra An analogue of truncation can be applied to polynomials. In t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |