|
Anti-symmetric Component
{{Di ...
Antisymmetric or skew-symmetric may refer to: * Antisymmetry in linguistics * Antisymmetry in physics * Antisymmetric relation in mathematics * Skew-symmetric graph * Self-complementary graph In mathematics, especially linear algebra, and in theoretical physics, the adjective antisymmetric (or skew-symmetric) is used for matrices, tensors, and other objects that change sign if an appropriate operation (e.g. matrix transposition) is performed. See: * Skew-symmetric matrix (a matrix ''A'' for which ) * Skew-symmetric bilinear form is a bilinear form ''B'' such that for all ''x'' and ''y''. * Antisymmetric tensor in matrices and index subsets. * "antisymmetric function" – odd function See also * Symmetry in mathematics Symmetry occurs not only in geometry, but also in other branches of mathematics. Symmetry is a type of invariance: the property that a mathematical object remains unchanged under a set of operations or transformations. Given a structured obje ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
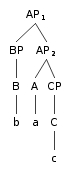
Antisymmetry
In linguistics, antisymmetry, is a theory of syntax described in Richard S. Kayne's 1994 book ''The Antisymmetry of Syntax''. Building upon X-bar theory, it proposes a universal, fundamental word order for phrases (Branching (linguistics), branching) across languages: specifier-head-complement. This means a phrase typically starts with an introductory element (Specifier (linguistics), specifier), followed by the core (Head (linguistics), head, often a verb or noun), and then additional information (Complement (linguistics), complement). The theory argues that any sentence structure that deviates from this order results from rearrangements (Syntactic movement, syntactic movements) of this underlying structure. For instance, a sentence like "Eat the cake quickly" might be analyzed as a rearrangement of a more basic specifier-head-complement structure "Quickly eat the cake". While Kayne proposes specifier-head-complement as the base order, some linguists have suggested alternative bas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dichromatic Symmetry
Dichromatic symmetry,Loeb, A.L. (1971). ''Color and Symmetry'', Wiley, New York, also referred to as antisymmetry,Shubnikov, A.V. (1951). ''Symmetry and antisymmetry of finite figures'', Izv. Akad. Nauk SSSR, Moscow black-and-white symmetry, magnetic symmetry, counterchange symmetry or dichroic symmetry, is a symmetry operation which reverses an object to its opposite. A more precise definition is "operations of antisymmetry transform objects possessing two possible values of a given property from one value to the other."Mackay, A.L. (1957). Extensions of space-group theory', Acta Crystallogr. 10, 543-548, Dichromatic symmetry refers specifically to two-coloured symmetry; this can be extended to three or more colours in which case it is termed polychromatic symmetry. A general term for dichromatic and polychromatic symmetry is simply colour symmetry. Dichromatic symmetry is used to describe Magnetic space group, magnetic crystals and in other areas of physics,Padmanabhan, H., Munr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antisymmetric Relation
In mathematics, a binary relation R on a set X is antisymmetric if there is no pair of ''distinct'' elements of X each of which is related by R to the other. More formally, R is antisymmetric precisely if for all a, b \in X, \text \,aRb\, \text \,a \neq b\, \text \,bRa\, \text, or equivalently, \text \,aRb\, \text \,bRa\, \text \,a = b. The definition of antisymmetry says nothing about whether aRa actually holds or not for any a. An antisymmetric relation R on a set X may be reflexive (that is, aRa for all a \in X), irreflexive (that is, aRa for no a \in X), or neither reflexive nor irreflexive. A relation is asymmetric if and only if it is both antisymmetric and irreflexive. Examples The divisibility relation on the natural numbers is an important example of an antisymmetric relation. In this context, antisymmetry means that the only way each of two numbers can be divisible by the other is if the two are, in fact, the same number; equivalently, if n and m are distinct and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Skew-symmetric Graph
In graph theory, a branch of mathematics, a skew-symmetric graph is a directed graph that is graph isomorphism, isomorphic to its own transpose graph, the graph formed by reversing all of its edges, under an isomorphism that is an involution (mathematics), involution without any Fixed point (mathematics), fixed points. Skew-symmetric graphs are identical to the Bipartite double cover, double covering graphs of bidirected graphs. Skew-symmetric graphs were first introduced under the name of ''antisymmetrical digraphs'' by , later as the double covering graphs of polar graphs by , and still later as the double covering graphs of bidirected graphs by . They arise in modeling the search for alternating paths and alternating cycles in algorithms for finding Matching (graph theory), matchings in graphs, in testing whether a still life (cellular automaton), still life pattern in Conway's Game of Life may be partitioned into simpler components, in graph drawing, and in the implication gra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Self-complementary Graph
In the mathematical field of graph theory, a self-complementary graph is a graph which is isomorphic to its complement. The simplest non-trivial self-complementary graphs are the path graph and the cycle graph. There is no known characterization of self-complementary graphs. Examples Every Paley graph is self-complementary. For example, the 3 × 3 rook's graph (the Paley graph of order nine) is self-complementary, by a symmetry that keeps the center vertex in place but exchanges the roles of the four side midpoints and four corners of the grid. All strongly regular self-complementary graphs with fewer than 37 vertices are Paley graphs; however, there are strongly regular graphs on 37, 41, and 49 vertices that are not Paley graphs. The Rado graph is an infinite self-complementary graph. Properties An self-complementary graph has exactly half as many edges of the complete graph, i.e., edges, and (if there is more than one vertex) it must have diameter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Algebra
Linear algebra is the branch of mathematics concerning linear equations such as :a_1x_1+\cdots +a_nx_n=b, linear maps such as :(x_1, \ldots, x_n) \mapsto a_1x_1+\cdots +a_nx_n, and their representations in vector spaces and through matrix (mathematics), matrices. Linear algebra is central to almost all areas of mathematics. For instance, linear algebra is fundamental in modern presentations of geometry, including for defining basic objects such as line (geometry), lines, plane (geometry), planes and rotation (mathematics), rotations. Also, functional analysis, a branch of mathematical analysis, may be viewed as the application of linear algebra to Space of functions, function spaces. Linear algebra is also used in most sciences and fields of engineering because it allows mathematical model, modeling many natural phenomena, and computing efficiently with such models. For nonlinear systems, which cannot be modeled with linear algebra, it is often used for dealing with first-order a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theoretical Physics
Theoretical physics is a branch of physics that employs mathematical models and abstractions of physical objects and systems to rationalize, explain, and predict List of natural phenomena, natural phenomena. This is in contrast to experimental physics, which uses experimental tools to probe these phenomena. The advancement of science generally depends on the interplay between experimental studies and theory. In some cases, theoretical physics adheres to standards of mathematical rigour while giving little weight to experiments and observations.There is some debate as to whether or not theoretical physics uses mathematics to build intuition and illustrativeness to extract physical insight (especially when normal experience fails), rather than as a tool in formalizing theories. This links to the question of it using mathematics in a less formally rigorous, and more intuitive or heuristic way than, say, mathematical physics. For example, while developing special relativity, Albert E ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix (math)
In mathematics, a matrix (: matrices) is a rectangular array or table of numbers, symbols, or expressions, with elements or entries arranged in rows and columns, which is used to represent a mathematical object or property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two-by-three matrix", a " matrix", or a matrix of dimension . Matrices are commonly used in linear algebra, where they represent linear maps. In geometry, matrices are widely used for specifying and representing geometric transformations (for example rotations) and coordinate changes. In numerical analysis, many computational problems are solved by reducing them to a matrix computation, and this often involves computing with matrices of huge dimensions. Matrices are used in most areas of mathematics and scientific fields, either directly, or through their use in geometry and numerical analysis. '' Square matr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects associated with a vector space. Tensors may map between different objects such as vectors, scalars, and even other tensors. There are many types of tensors, including scalars and vectors (which are the simplest tensors), dual vectors, multilinear maps between vector spaces, and even some operations such as the dot product. Tensors are defined independent of any basis, although they are often referred to by their components in a basis related to a particular coordinate system; those components form an array, which can be thought of as a high-dimensional matrix. Tensors have become important in physics because they provide a concise mathematical framework for formulating and solving physics problems in areas such as mechanics ( stress, elasticity, quantum mechanics, fluid mechanics, moment of inertia, ...), electrodynamics ( electromagnetic ten ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transposition (mathematics)
In mathematics, and in particular in group theory, a cyclic permutation is a permutation consisting of a single cycle. In some cases, cyclic permutations are referred to as cycles; if a cyclic permutation has ''k'' elements, it may be called a ''k''-cycle. Some authors widen this definition to include permutations with fixed points in addition to at most one non-trivial cycle. In Permutation#Cycle notation, cycle notation, cyclic permutations are denoted by the list of their elements enclosed with parentheses, in the order to which they are permuted. For example, the permutation (1 3 2 4) that sends 1 to 3, 3 to 2, 2 to 4 and 4 to 1 is a 4-cycle, and the permutation (1 3 2)(4) that sends 1 to 3, 3 to 2, 2 to 1 and 4 to 4 is considered a 3-cycle by some authors. On the other hand, the permutation (1 3)(2 4) that sends 1 to 3, 3 to 1, 2 to 4 and 4 to 2 is not a cyclic permutation because it separately permutes the pairs and . For the wider definition of a cyclic permutation, allowi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Skew-symmetric Matrix
In mathematics, particularly in linear algebra, a skew-symmetric (or antisymmetric or antimetric) matrix is a square matrix whose transpose equals its negative. That is, it satisfies the condition In terms of the entries of the matrix, if a_ denotes the entry in the i-th row and j-th column, then the skew-symmetric condition is equivalent to Example The matrix A = \begin 0 & 2 & -45 \\ -2 & 0 & -4 \\ 45 & 4 & 0 \end is skew-symmetric because A^\textsf = \begin 0 & -2 & 45 \\ 2 & 0 & 4 \\ -45 & -4 & 0 \end = -A . Properties Throughout, we assume that all matrix entries belong to a field \mathbb whose characteristic is not equal to 2. That is, we assume that , where 1 denotes the multiplicative identity and 0 the additive identity of the given field. If the characteristic of the field is 2, then a skew-symmetric matrix is the same thing as a symmetric matrix. * The sum of two skew-symmetric matrices is skew-symmetric. * A scalar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bilinear Form
In mathematics, a bilinear form is a bilinear map on a vector space (the elements of which are called '' vectors'') over a field ''K'' (the elements of which are called '' scalars''). In other words, a bilinear form is a function that is linear in each argument separately: * and * and The dot product on \R^n is an example of a bilinear form which is also an inner product. An example of a bilinear form that is not an inner product would be the four-vector product. The definition of a bilinear form can be extended to include modules over a ring, with linear maps replaced by module homomorphisms. When is the field of complex numbers , one is often more interested in sesquilinear forms, which are similar to bilinear forms but are conjugate linear in one argument. Coordinate representation Let be an - dimensional vector space with basis . The matrix ''A'', defined by is called the ''matrix of the bilinear form'' on the basis . If the matrix represents a ve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |