|
Analytic Signal
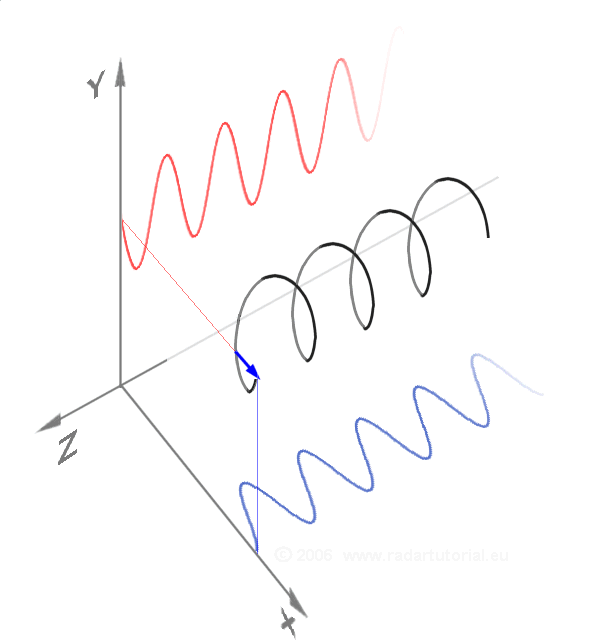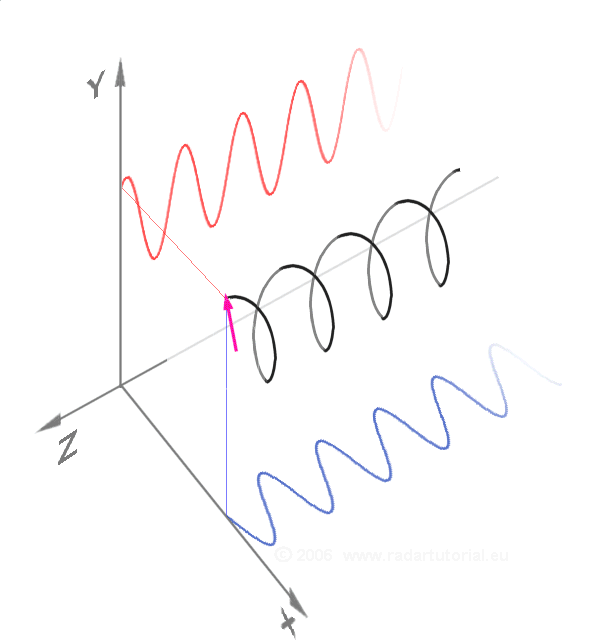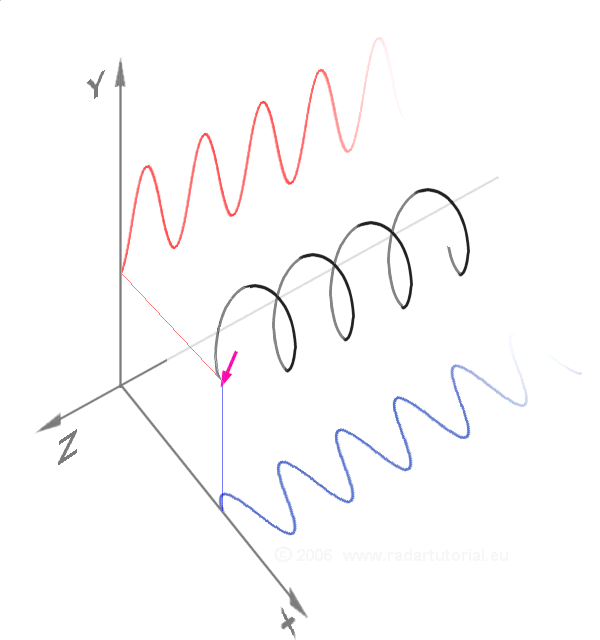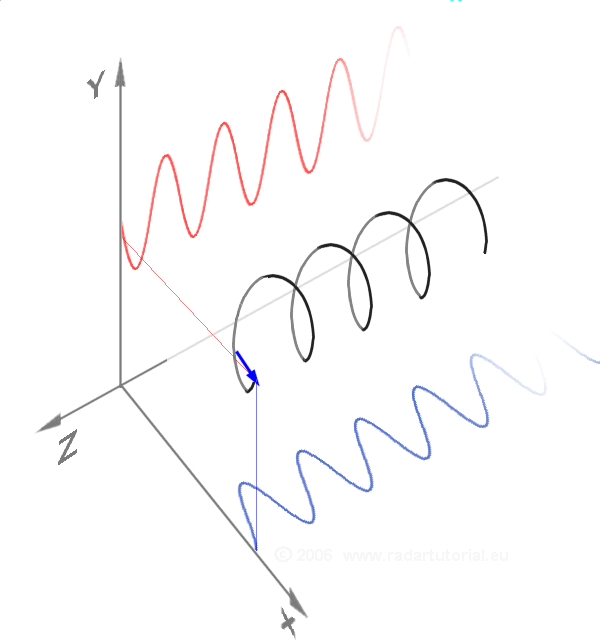
In mathematics and signal processing, an analytic signal is a complex-valued function that has no negative frequency components. The real and imaginary parts of an analytic signal are real-valued functions related to each other by the Hilbert transform. The analytic representation of a real-valued function is an ''analytic signal'', comprising the original function and its Hilbert transform. This representation facilitates many mathematical manipulations. The basic idea is that the negative frequency components of the Fourier transform (or spectrum) of a real-valued function are superfluous, due to the Hermitian symmetry of such a spectrum. These negative frequency components can be discarded with no loss of information, provided one is willing to deal with a complex-valued function instead. That makes certain attributes of the function more accessible and facilitates the derivation of modulation and demodulation techniques, such as single-sideband. As long as the manip ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Hilbert Transform
In mathematics and signal processing, the Hilbert transform is a specific singular integral that takes a function, of a real variable and produces another function of a real variable . The Hilbert transform is given by the Cauchy principal value of the convolution with the function 1/(\pi t) (see ). The Hilbert transform has a particularly simple representation in the frequency domain: It imparts a phase shift of ±90° (/2 radians) to every frequency component of a function, the sign of the shift depending on the sign of the frequency (see ). The Hilbert transform is important in signal processing, where it is a component of the Analytic signal, analytic representation of a real-valued signal . The Hilbert transform was first introduced by David Hilbert in this setting, to solve a special case of the Riemann–Hilbert problem for analytic functions. Definition The Hilbert transform of can be thought of as the convolution of with the function , known as the Cauchy ker ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Euler's Formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that, for any real number , one has e^ = \cos x + i \sin x, where is the base of the natural logarithm, is the imaginary unit, and and are the trigonometric functions cosine and sine respectively. This complex exponential function is sometimes denoted ("cosine plus ''i'' sine"). The formula is still valid if is a complex number, and is also called ''Euler's formula'' in this more general case. Euler's formula is ubiquitous in mathematics, physics, chemistry, and engineering. The physicist Richard Feynman called the equation "our jewel" and "the most remarkable formula in mathematics". When , Euler's formula may be rewritten as or , which is known as Euler's identity. History In 1714, the English mathematician Roger Cotes prese ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Carrier Frequency
In telecommunications, a carrier wave, carrier signal, or just carrier, is a periodic waveform (usually sinusoidal) that conveys information through a process called ''modulation''. One or more of the wave's properties, such as amplitude or frequency, are modified by an information bearing signal, called the ''message signal'' or ''modulation signal''. The carrier frequency is usually much higher than the message signal frequency; this is because it is usually impractical to transmit signals with low frequencies over long distances (due to attenuation). The purpose of the carrier is usually either to transmit the information through space as an electromagnetic wave (as in radio communication), or to allow several carriers at different frequencies to share a common physical transmission medium by frequency division multiplexing (as in a cable television system). The term originated in radio communication, where the carrier wave creates the waves which carry the information (mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Passband Signal
A passband is the range of frequencies or wavelengths that can pass through a filter. For example, a radio receiver contains a bandpass filter to select the frequency of the desired radio signal out of all the radio waves picked up by its antenna. The passband of a receiver is the range of frequencies it can receive when it is tuned into the desired frequency as in a radio station or television channel. A bandpass-filtered signal (that is, a signal with energy only in a passband), is known as a bandpass signal, in contrast to a baseband signal. The bandpass filter usually has two band-stop filters. Filters In telecommunications, optics, and acoustics, a passband (a band-pass filtered signal) is the portion of the frequency spectrum that is transmitted (with minimum relative loss or maximum relative gain) by some filtering device. In other words, it is a ''band'' of frequencies which ''pass''es through some filter or a set of filters. The accompanying figure shows a sc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Baseband
In telecommunications and signal processing, baseband is the range of frequencies occupied by a signal that has not been modulated to higher frequencies. Baseband signals typically originate from transducers, converting some other variable into an electrical signal. For example, the electronic output of a microphone is a baseband signal that is analogous to the applied voice audio. In conventional analog radio broadcasting, the baseband audio signal is used to modulate an RF carrier signal of a much higher frequency. A baseband signal may have frequency components going all the way down to the DC bias, or at least it will have a high ratio bandwidth. A modulated baseband signal is called a passband signal. This occupies a higher range of frequencies and has a lower ratio and fractional bandwidth. Various uses Baseband signal A ''baseband signal'' or ''lowpass signal'' is a signal that can include frequencies that are very near zero, by comparison with its highest ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
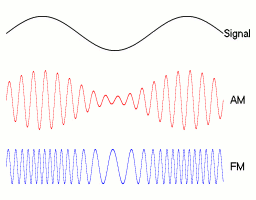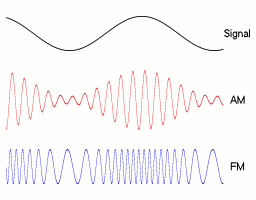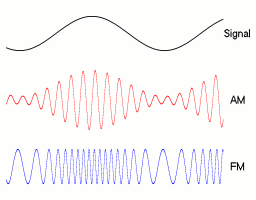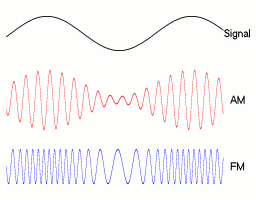 |
Amplitude Modulation
Amplitude modulation (AM) is a signal modulation technique used in electronic communication, most commonly for transmitting messages with a radio wave. In amplitude modulation, the instantaneous amplitude of the wave is varied in proportion to that of the message signal, such as an audio signal. This technique contrasts with angle modulation, in which either the frequency of the carrier wave is varied, as in frequency modulation, or its Phase (waves), phase, as in phase modulation. AM was the earliest modulation method used for transmitting audio in radio broadcasting. It was developed during the first quarter of the 20th century beginning with Roberto Landell de Moura and Reginald Fessenden's radiotelephone experiments in 1900. This original form of AM is sometimes called double-sideband amplitude modulation (DSBAM), because the standard method produces sidebands on either side of the carrier frequency. Single-sideband modulation uses bandpass filters to eliminate one of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Modulation
Signal modulation is the process of varying one or more properties of a periodic waveform in electronics and telecommunication for the purpose of transmitting information. The process encodes information in form of the modulation or message signal onto a carrier signal to be transmitted. For example, the message signal might be an audio signal representing sound from a microphone, a video signal representing moving images from a video camera, or a digital signal representing a sequence of binary digits, a bitstream from a computer. This carrier wave usually has a much higher frequency than the message signal does. This is because it is impractical to transmit signals with low frequencies. Generally, receiving a radio wave requires a radio antenna with a length that is one-fourth of the wavelength of the transmitted wave. For low frequency radio waves, wavelength is on the scale of kilometers and building such a large antenna is not practical. Another purpose of modulation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Hertz
The hertz (symbol: Hz) is the unit of frequency in the International System of Units (SI), often described as being equivalent to one event (or Cycle per second, cycle) per second. The hertz is an SI derived unit whose formal expression in terms of SI base units is 1/s or s−1, meaning that one hertz is one per second or the Inverse second, reciprocal of one second. It is used only in the case of periodic events. It is named after Heinrich Hertz, Heinrich Rudolf Hertz (1857–1894), the first person to provide conclusive proof of the existence of electromagnetic waves. For high frequencies, the unit is commonly expressed in metric prefix, multiples: kilohertz (kHz), megahertz (MHz), gigahertz (GHz), terahertz (THz). Some of the unit's most common uses are in the description of periodic waveforms and musical tones, particularly those used in radio- and audio-related applications. It is also used to describe the clock speeds at which computers and other electronics are driven. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Instantaneous Phase
Instantaneous phase and frequency are important concepts in signal processing that occur in the context of the representation and analysis of time-varying functions. The instantaneous phase (also known as local phase or simply phase) of a ''complex-valued'' function ''s''(''t''), is the real-valued function: :\varphi(t) = \arg\, where arg is the Argument (complex analysis), complex argument function. The instantaneous frequency is the temporal rate of change of the instantaneous phase. And for a ''real-valued'' function ''s''(''t''), it is determined from the function's analytic signal, analytic representation, ''s''a(''t''): :\begin \varphi(t) &= \arg\ \\[4pt] &= \arg\, \end where \hat(t) represents the Hilbert transform of ''s''(''t''). When ''φ''(''t'') is constrained to its principal value, either the interval or , it is called ''wrapped phase''. Otherwise it is called ''unwrapped phase'', which is a continuous function of argument ''t'', assuming ''s''a(''t' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |