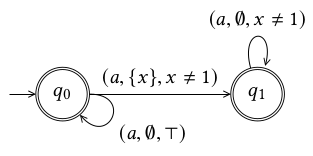|
Alternating Timed Automaton
In automata theory, an alternating timed automaton (ATA) is a mix of both timed automaton and alternating finite automaton. That is, it is a sort of automata which can measure time and in which there exists universal and existential transition. ATAs are more expressive than timed automaton. one clock alternating timed automaton (OCATA) is the restriction of ATA allowing the use of a single clock. OCATAs allow to express timed languages which can not be expressed using timed-automaton. Definition An alternating timed automaton is defined as a timed automaton, where the transitions are more complex. Difference from a timed-automaton Given a set X, let \mathcal B^+(X) the set of positive Boolean combination of elements of X. I.e. the set containing the elements of X, and containing \phi\land\psi and \phi\lor\psi, for \phi,\psi\in\mathcal B^+(X). For each letter a and location \ell, let \mathcal B_ be a set of clock constraints such that their zones partition \mathbb R_^, with , ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Automata Theory
Automata theory is the study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science. The word ''automata'' comes from the Greek word αὐτόματος, which means "self-acting, self-willed, self-moving". An automaton (automata in plural) is an abstract self-propelled computing device which follows a predetermined sequence of operations automatically. An automaton with a finite number of states is called a Finite Automaton (FA) or Finite-State Machine (FSM). The figure on the right illustrates a finite-state machine, which is a well-known type of automaton. This automaton consists of states (represented in the figure by circles) and transitions (represented by arrows). As the automaton sees a symbol of input, it makes a transition (or jump) to another state, according to its transition function, which takes the previous state and current input symbol as its arguments. Automata the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Timed Automaton
In automata theory, a timed automaton is a finite automaton extended with a finite set of real-valued clocks. During a run of a timed automaton, clock values increase all with the same speed. Along the transitions of the automaton, clock values can be compared to integers. These comparisons form guards that may enable or disable transitions and by doing so constrain the possible behaviors of the automaton. Further, clocks can be reset. Timed automata are a sub-class of a type hybrid automata. Timed automata can be used to model and analyse the timing behavior of computer systems, e.g., real-time systems or networks. Methods for checking both safety and liveness properties have been developed and intensively studied over the last 20 years. It has been shown that the state reachability problem for timed automata is decidable,Rajeev Alur, David L. Dill. 199A Theory of Timed Automata In Theoretical Computer Science, vol. 126, 183–235, pp. 194–1955 which makes this an interesting s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alternating Finite Automaton
In automata theory, an alternating finite automaton (AFA) is a nondeterministic finite automaton whose transitions are divided into ''existential'' and ''universal'' transitions. For example, let ''A'' be an alternating automaton. * For an existential transition (q, a, q_1 \vee q_2), ''A'' nondeterministically chooses to switch the state to either q_1 or q_2, reading ''a''. Thus, behaving like a regular nondeterministic finite automaton. * For a universal transition (q, a, q_1 \wedge q_2), ''A'' moves to q_1 and q_2, reading ''a'', simulating the behavior of a parallel machine. Note that due to the universal quantification a run is represented by a run ''tree''. ''A'' accepts a word ''w'', if there ''exists'' a run tree on ''w'' such that ''every'' path ends in an accepting state. A basic theorem states that any AFA is equivalent to a deterministic finite automaton (DFA), hence AFAs accept exactly the regular languages. An alternative model which is frequently used is the one where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Timed Language
In model checking, a subfield of computer science, a timed word is an extension of the notion of words, in a formal language, in which each letter is associated with a positive time tag. The sequence of time tag must be non-decreasing, which intuitively means that letters are received. For example, a system receiving a word over a network may associate to each letter the time at which the letter is received. The non-decreasing condition here means that the letters are received in the correct order. A timed language is a set of timed words. Example Consider an elevator. What is formally called a letter is could be in fact an information such that "someone press the button on the 2nd floor", or "the doors opened on the third floor". In this case, a timed word is a sequence of actions taken by the elevators and its users, with time stamps to recall those actions. The timed word can then be analyzed by formal method to check whether a property such that "each time the elevator is call ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zone (convex Polytope)
In model checking, a field of computer science, a difference bound matrix (DBM) is a data structure used to represent some convex polytopes called zones. This structure can be used to efficiently implement some geometrical operations over zones, such as testing emptyness, inclusion, equality, and computing the intersection and the sum of two zones. It is, for example, used in the Uppaal model checker; where it is also distributed as an independent library. More precisely, there is a notion of canonical DBM; there is a one-to-one relation between canonical DBMs and zones and from each DBM a canonical equivalent DBM can be efficiently computed. Thus, equality of zone can be tested by checking for equality of canonical DBMs. Zone A difference bound matrix is used to represents some kind of convex polytopes. Those polytopes are called zone. They are now defined. Formally, a zone is defined by equations of the form x\le c, x\ge c, x_1\le x_2+c and x_1\ge x_2+c, with x_1 and x_2 some ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite Set
In mathematics, particularly set theory, a finite set is a set that has a finite number of elements. Informally, a finite set is a set which one could in principle count and finish counting. For example, :\ is a finite set with five elements. The number of elements of a finite set is a natural number (possibly zero) and is called the '' cardinality (or the cardinal number)'' of the set. A set that is not a finite set is called an '' infinite set''. For example, the set of all positive integers is infinite: :\. Finite sets are particularly important in combinatorics, the mathematical study of counting. Many arguments involving finite sets rely on the pigeonhole principle, which states that there cannot exist an injective function from a larger finite set to a smaller finite set. Definition and terminology Formally, a set is called finite if there exists a bijection :f\colon S\to\ for some natural number . The number is the set's cardinality, denoted as . The empty s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clock (model Checking)
In model checking, a subfield of computer science, a clock is a mathematical object used to model time. More precisely, a clock measures how much time passed since a particular event occurs, in this sense, a clock is more precisely an abstraction of a stopwatch. In a model of some particular program, the value of the clock may either be the time since the program was started, or the time since a particular event occurred in the program. Those clocks are used in the definition of timed automaton, signal automaton, timed propositional temporal logic and clock temporal logic. They are also used in programs such as UPPAAL which implement timed automata. Generally, the model of a system uses many clocks. Those multiple clocks are required in order to track a bounded number of events. All of those clocks are synchronized. That means that the difference in value between two fixed clocks is constant until one of them is restarted. In the language of electronics, it means that clock's jitter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Disjunctive Normal Form
In boolean logic, a disjunctive normal form (DNF) is a canonical normal form of a logical formula consisting of a disjunction of conjunctions; it can also be described as an OR of ANDs, a sum of products, or (in philosophical logic) a ''cluster concept''. As a normal form, it is useful in automated theorem proving. Definition A logical formula is considered to be in DNF if it is a disjunction of one or more conjunctions of one or more literals. A DNF formula is in full disjunctive normal form if each of its variables appears exactly once in every conjunction. As in conjunctive normal form (CNF), the only propositional operators in DNF are and (\wedge), or (\vee), and not (\neg). The ''not'' operator can only be used as part of a literal, which means that it can only precede a propositional variable. The following is a context-free grammar for DNF: # ''DNF'' → (''Conjunction'') \vee ''DNF'' # ''DNF'' → (''Conjunction'') # ''Conjunction'' → ''Literal'' \wedge ''Conjunc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Game Theory
Game theory is the study of mathematical models of strategic interactions among rational agents. Myerson, Roger B. (1991). ''Game Theory: Analysis of Conflict,'' Harvard University Press, p.&nbs1 Chapter-preview links, ppvii–xi It has applications in all fields of social science, as well as in logic, systems science and computer science. Originally, it addressed two-person zero-sum games, in which each participant's gains or losses are exactly balanced by those of other participants. In the 21st century, game theory applies to a wide range of behavioral relations; it is now an umbrella term for the science of logical decision making in humans, animals, as well as computers. Modern game theory began with the idea of mixed-strategy equilibria in two-person zero-sum game and its proof by John von Neumann. Von Neumann's original proof used the Brouwer fixed-point theorem on continuous mappings into compact convex sets, which became a standard method in game theory and m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rooted Tree
In graph theory, a tree is an undirected graph in which any two vertices are connected by ''exactly one'' path, or equivalently a connected acyclic undirected graph. A forest is an undirected graph in which any two vertices are connected by ''at most one'' path, or equivalently an acyclic undirected graph, or equivalently a disjoint union of trees. A polytreeSee . (or directed tree or oriented treeSee .See . or singly connected networkSee .) is a directed acyclic graph (DAG) whose underlying undirected graph is a tree. A polyforest (or directed forest or oriented forest) is a directed acyclic graph whose underlying undirected graph is a forest. The various kinds of data structures referred to as trees in computer science have underlying graphs that are trees in graph theory, although such data structures are generally rooted trees. A rooted tree may be directed, called a directed rooted tree, either making all its edges point away from the root—in which case it is called a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recursive Language
In mathematics, logic and computer science, a formal language (a set of finite sequences of symbols taken from a fixed alphabet) is called recursive if it is a recursive subset of the set of all possible finite sequences over the alphabet of the language. Equivalently, a formal language is recursive if there exists a total Turing machine (a Turing machine that halts for every given input) that, when given a finite sequence of symbols as input, accepts it if it belongs to the language and rejects it otherwise. Recursive languages are also called decidable. The concept of decidability may be extended to other models of computation. For example, one may speak of languages decidable on a non-deterministic Turing machine. Therefore, whenever an ambiguity is possible, the synonym used for "recursive language" is Turing-decidable language, rather than simply ''decidable''. The class of all recursive languages is often called R, although this name is also used for the class RP. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |