|
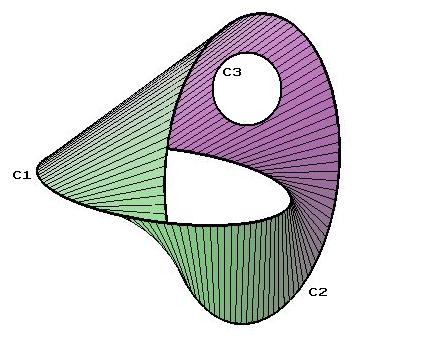
Algebraic Link
In the mathematical field of knot theory In the mathematical field of topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined so it cannot ..., an algebraic link is a link that can be decomposed by Conway spheres into 2-tangles. Algebraic links are also called arborescent links. Although algebraic links and algebraic tangles were originally defined by John H. Conway as having two pairs of open ends, they were subsequently generalized to more pairs.. References Links (knot theory) {{knottheory-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Borromean Link Diagram
Algebraic may refer to any subject related to algebra in mathematics and related branches like algebraic number theory and algebraic topology. The word algebra itself has several meanings. Algebraic may also refer to: * Algebraic data type, a datatype in computer programming each of whose values is data from other datatypes wrapped in one of the constructors of the datatype * Algebraic numbers, a complex number that is a root of a non-zero polynomial in one variable with integer coefficients * Algebraic functions, functions satisfying certain polynomials * Algebraic element, an element of a field extension which is a root of some polynomial over the base field * Algebraic extension, a field extension such that every element is an algebraic element over the base field * Algebraic definition, a definition in mathematical logic which is given using only equalities between terms * Algebraic structure, a set with one or more finitary operations defined on it * Algebraic, the order of en ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Knot Theory
In the mathematical field of topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined so it cannot be undone, the simplest knot being a ring (or "unknot"). In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, \mathbb^3 (in topology, a circle is not bound to the classical geometric concept, but to all of its homeomorphisms). Two mathematical knots are equivalent if one can be transformed into the other via a deformation of \mathbb^3 upon itself (known as an ambient isotopy); these transformations correspond to manipulations of a knotted string that do not involve cutting it or passing through itself. Knots can be described in various ways. Using different description methods, there may be more than one description of the same knot. For example, a common method of describing a knot is a planar d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Link (knot Theory)
In mathematical knot theory, a link is a collection of knots which do not intersect, but which may be linked (or knotted) together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory. Implicit in this definition is that there is a ''trivial'' reference link, usually called the unlink, but the word is also sometimes used in context where there is no notion of a trivial link. For example, a co-dimension 2 link in 3-dimensional space is a subspace of 3-dimensional Euclidean space (or often the 3-sphere) whose connected components are homeomorphic to circle A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is const ...s. The simplest nontrivial example of a link with more than one component is called the Hop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conway Sphere
In mathematical knot theory, a Conway sphere, named after John Horton Conway, is a 2-sphere intersecting a given knot or link in a 3-manifold transversely in four points. In a knot diagram, a Conway sphere can be represented by a simple closed curve crossing four points of the knot, the cross-section of the sphere; such a curve does not always exist for an arbitrary knot diagram of a knot with a Conway sphere, but it is always possible to choose a diagram for the knot in which the sphere can be depicted in this way. A Conway sphere is ''essential'' if it is incompressible in the knot complement In mathematics, the knot complement of a tame knot ''K'' is the space where the knot is not. If a knot is embedded in the 3-sphere, then the complement is the 3-sphere minus the space near the knot. To make this precise, suppose that ''K'' is a .... Sometimes, this condition is included in the definition of Conway spheres. References Knot theory John Horton Conway {{knotth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tangle (mathematics)
In mathematics, a tangle is generally one of two related concepts: * In John Conway's definition, an ''n''-tangle is a proper embedding of the disjoint union of ''n'' arcs into a 3-ball; the embedding must send the endpoints of the arcs to 2''n'' marked points on the ball's boundary. * In link theory, a tangle is an embedding of ''n'' arcs and ''m'' circles into \mathbf^2 \times ,1/math> – the difference from the previous definition is that it includes circles as well as arcs, and partitions the boundary into two (isomorphic) pieces, which is algebraically more convenient – it allows one to add tangles by stacking them, for instance. (A quite different use of 'tangle' appears in Graph minors X. Obstructions to tree-decomposition by N. Robertson and P. D. Seymour, ''Journal of Combinatorial Theory'' B 52 (1991) 153–190, who used it to describe separation in graphs. This usage has been extended to matroids.) The balance of this article discusses Conway's sense of tangles; f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pacific Journal Of Mathematics
The Pacific Journal of Mathematics is a mathematics research journal supported by several universities and research institutes, and currently published on their behalf by Mathematical Sciences Publishers, a non-profit academic publishing organisation, and the University of California, Berkeley. It was founded in 1951 by František Wolf and Edwin F. Beckenbach and has been published continuously since, with five two-issue volumes per year and 12 issues per year. Full-text PDF versions of all journal articles are available on-line via the journal's website with a subscription. The journal is incorporated as a 501(c)(3) organization A 501(c)(3) organization is a United States corporation, Trust (business), trust, unincorporated association or other type of organization exempt from federal income tax under section 501(c)(3) of Title 26 of the United States Code. It is one of t .... References Mathematics journals Publications established in 1951 Mathematical Sciences Publish ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Memoirs Of The American Mathematical Society
''Memoirs of the American Mathematical Society'' is a mathematical journal published in six volumes per year, totalling approximately 33 individually bound numbers, by the American Mathematical Society. It is intended to carry papers on new mathematical research between 80 and 200 pages in length. Usually, a bound number consists of a single paper, i.e., it is a monograph. The journal is indexed by Mathematical Reviews, Zentralblatt MATH, Science Citation Index, Research Alert, CompuMath Citation Index, and Current Contents. Other journals from the AMS * ''Bulletin of the American Mathematical Society'' * ''Journal of the American Mathematical Society'' * ''Notices of the American Mathematical Society'' * ''Proceedings of the American Mathematical Society'' * ''Transactions of the American Mathematical Society The ''Transactions of the American Mathematical Society'' is a monthly peer-reviewed scientific journal of mathematics published by the American Mathematical Society. It ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John H
John is a common English name and surname: * John (given name) * John (surname) John may also refer to: New Testament Works * Gospel of John, a title often shortened to John * First Epistle of John, often shortened to 1 John * Second Epistle of John, often shortened to 2 John * Third Epistle of John, often shortened to 3 John People * John the Baptist (died c. AD 30), regarded as a prophet and the forerunner of Jesus Christ * John the Apostle (lived c. AD 30), one of the twelve apostles of Jesus * John the Evangelist, assigned author of the Fourth Gospel, once identified with the Apostle * John of Patmos, also known as John the Divine or John the Revelator, the author of the Book of Revelation, once identified with the Apostle * John the Presbyter, a figure either identified with or distinguished from the Apostle, the Evangelist and John of Patmos Other people with the given name Religious figures * John, father of Andrew the Apostle and Saint Peter * P ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |