|
Accelerated Life Testing
Accelerated life testing is the process of testing a product by subjecting it to conditions ( stress, strain, temperatures, voltage, vibration rate, pressure etc.) in excess of its normal service parameters in an effort to uncover faults and potential modes of failure in a short amount of time. By analyzing the product's response to such tests, engineers can make predictions about the service life and maintenance intervals of a product. In polymers, testing may be done at elevated temperatures to produce a result in a shorter amount of time than it could be produced at ambient temperatures. Many mechanical properties of polymers have an Arrhenius type relationship with respect to time and temperature (for example, creep, stress relaxation, and tensile properties). If one conducts short tests at elevated temperatures, that data can be used to extrapolate the behavior of the polymer at room temperature, avoiding the need to do lengthy, and hence expensive tests. Purpose ALT is p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stress (mechanics)
In continuum mechanics, stress is a physical quantity that describes forces present during deformation. For example, an object being pulled apart, such as a stretched elastic band, is subject to ''tensile'' stress and may undergo elongation. An object being pushed together, such as a crumpled sponge, is subject to ''compressive'' stress and may undergo shortening. The greater the force and the smaller the cross-sectional area of the body on which it acts, the greater the stress. Stress has dimension of force per area, with SI units of newtons per square meter (N/m2) or pascal (Pa). Stress expresses the internal forces that neighbouring particles of a continuous material exert on each other, while ''strain'' is the measure of the relative deformation of the material. For example, when a solid vertical bar is supporting an overhead weight, each particle in the bar pushes on the particles immediately below it. When a liquid is in a closed container under pressure, each ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weibull Distribution
In probability theory and statistics, the Weibull distribution is a continuous probability distribution. It models a broad range of random variables, largely in the nature of a time to failure or time between events. Examples are maximum one-day rainfalls and the time a user spends on a web page. The distribution is named after Swedish mathematician Waloddi Weibull, who described it in detail in 1939, although it was first identified by René Maurice Fréchet and first applied by to describe a Particle-size distribution, particle size distribution. Definition Standard parameterization The probability density function of a Weibull random variable is : f(x;\lambda,k) = \begin \frac\left(\frac\right)^e^, & x\geq0 ,\\ 0, & x 0 is the ''shape parameter'' and λ > 0 is the ''scale parameter'' of the distribution. Its Cumulative distribution function#Complementary cumulative distribution function (tail distribution), complementary cumulative distribution function is a stretch ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fatigue Testing
Fatigue testing is a specialised form of mechanical testing that is performed by applying cyclic loading to a ''coupon'' or structure. These tests are used either to generate fatigue life and crack growth data, identify critical locations or demonstrate the safety of a structure that may be susceptible to fatigue. Fatigue tests are used on a range of components from coupons through to full size test articles such as automobiles and aircraft. Fatigue tests on coupons are typically conducted using servo hydraulic test machines which are capable of applying large ''variable amplitude'' cyclic loads. ''Constant amplitude'' testing can also be applied by simpler oscillating machines. The ''fatigue life'' of a coupon is the number of cycles it takes to break the coupon. This data can be used for creating stress-life or strain-life curves. The rate of crack growth in a coupon can also be measured, either during the test or afterward using fractography. Testing of coupons can also be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cox Model
Proportional hazards models are a class of survival models in statistics. Survival models relate the time that passes, before some event occurs, to one or more covariates that may be associated with that quantity of time. In a proportional hazards model, the unique effect of a unit increase in a covariate is multiplicative with respect to the hazard rate. The hazard rate at time t is the probability per short time d''t'' that an event will occur between t and t + dt given that up to time t no event has occurred yet. For example, taking a drug may halve one's hazard rate for a stroke occurring, or, changing the material from which a manufactured component is constructed, may double its hazard rate for failure. Other types of survival models such as accelerated failure time models do not exhibit proportional hazards. The accelerated failure time model describes a situation where the biological or mechanical life history of an event is accelerated (or decelerated). Background ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
AFT Model
In the statistical area of survival analysis, an accelerated failure time model (AFT model) is a parametric model that provides an alternative to the commonly used proportional hazards models. Whereas a proportional hazards model assumes that the effect of a covariate is to multiply the hazard by some constant, an AFT model assumes that the effect of a covariate is to accelerate or decelerate the life course of a disease by some constant. There is strong basic science evidence from ''C. elegans'' experiments by Stroustrup et al. indicating that AFT models are the correct model for biological survival processes. Model specification In full generality, the accelerated failure time model can be specified as :: \lambda(t, \theta)=\theta\lambda_0(\theta t) where \theta denotes the joint effect of covariates, typically \theta=\exp(- beta_1X_1 + \cdots + \beta_pX_p. (Specifying the regression coefficients with a negative sign implies that high values of the covariates ''increase'' the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Accelerated Aging
Accelerated aging is testing that uses aggravated conditions of heat, humidity, oxygen, sunlight, vibration, etc. to speed up the normal aging processes of items. It is used to help determine the long-term effects of expected levels of stress within a shorter time, usually in a laboratory by controlled standard test methods. It is used to estimate the useful lifespan of a product or its shelf life when actual lifespan data is unavailable. This occurs with products that have not existed long enough to have gone through their useful lifespan: for example, a new type of car engine or a new polymer for replacement joints. Physical testing or chemical testing is carried out by subjecting the product to * representative levels of stress for long time periods, * unusually high levels of stress used to accelerate the effects of natural aging, or * levels of stress that intentionally force failures (for further analysis). Mechanical parts are run at very high speed, far in excess of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reliability (engineering)
Reliability engineering is a sub-discipline of systems engineering that emphasizes the ability of equipment to function without failure. Reliability is defined as the probability that a product, system, or service will perform its intended function adequately for a specified period of time, OR will operate in a defined environment without failure. Reliability is closely related to availability, which is typically described as the ability of a component or system to function at a specified moment or interval of time. The ''reliability function'' is theoretically defined as the probability of success. In practice, it is calculated using different techniques, and its value ranges between 0 and 1, where 0 indicates no probability of success while 1 indicates definite success. This probability is estimated from detailed (physics of failure) analysis, previous data sets, or through reliability testing and reliability modeling. Availability, testability, maintainability, and maintenance ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Service Life
A product's service life is its period of use in service. Several related terms describe more precisely a product's life, from the point of manufacture, storage, and distribution, and eventual use. Service life has been defined as "a product's total life in use from the point of sale to the point of discard" and distinguished from replacement life, "the period after which the initial purchaser returns to the shop for a replacement". Determining a product's expected service life as part of business policy ( product life cycle management) involves using tools and calculations from maintainability and reliability analysis. Service life represents a commitment made by the item's manufacturer and is usually specified as a median. It is the time that any manufactured item can be expected to be "serviceable" or supported by its manufacturer. Service life is not to be confused with '' shelf life'', which deals with storage time, or with technical life, which is the maximum period ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Product Management
Product management is the business process of planning, developing, launching, and managing a product or service. It includes the entire lifecycle of a product, from ideation to development to go to market. Product managers are responsible for ensuring that a product meets the needs of its target market and contributes to the business strategy, while managing a product or products at all stages of the product lifecycle. Software product management adapts the fundamentals of product management for digital products. History The concept of product management originates from a 1931 memo by Procter & Gamble President Neil H. McElroy. McElroy, requesting additional employees focused on brand management, needed "Brand Men" who would take on the role of managing products, packaging, positioning, distribution, and sales performance. The memo defined a brand man's work as: * Study carefully the shipments of his brands by units. * Where brand development is heavy ... examine care ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Research And Development
Research and development (R&D or R+D), known in some countries as OKB, experiment and design, is the set of innovative activities undertaken by corporations or governments in developing new services or products. R&D constitutes the first stage of development of a potential new service or the production process. Although R&D activities may differ across businesses, the primary goal of an R&D department is to new product development, develop new products and services. R&D differs from the vast majority of corporate activities in that it is not intended to yield immediate profit, and generally carries greater risk and an uncertain return on investment. R&D is crucial for acquiring larger shares of the market through new products. ''R&D&I'' represents R&D with innovation. Background New product design and development is often a crucial factor in the survival of a company. In a global industrial landscape that is changing fast, firms must continually revise their design and range of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
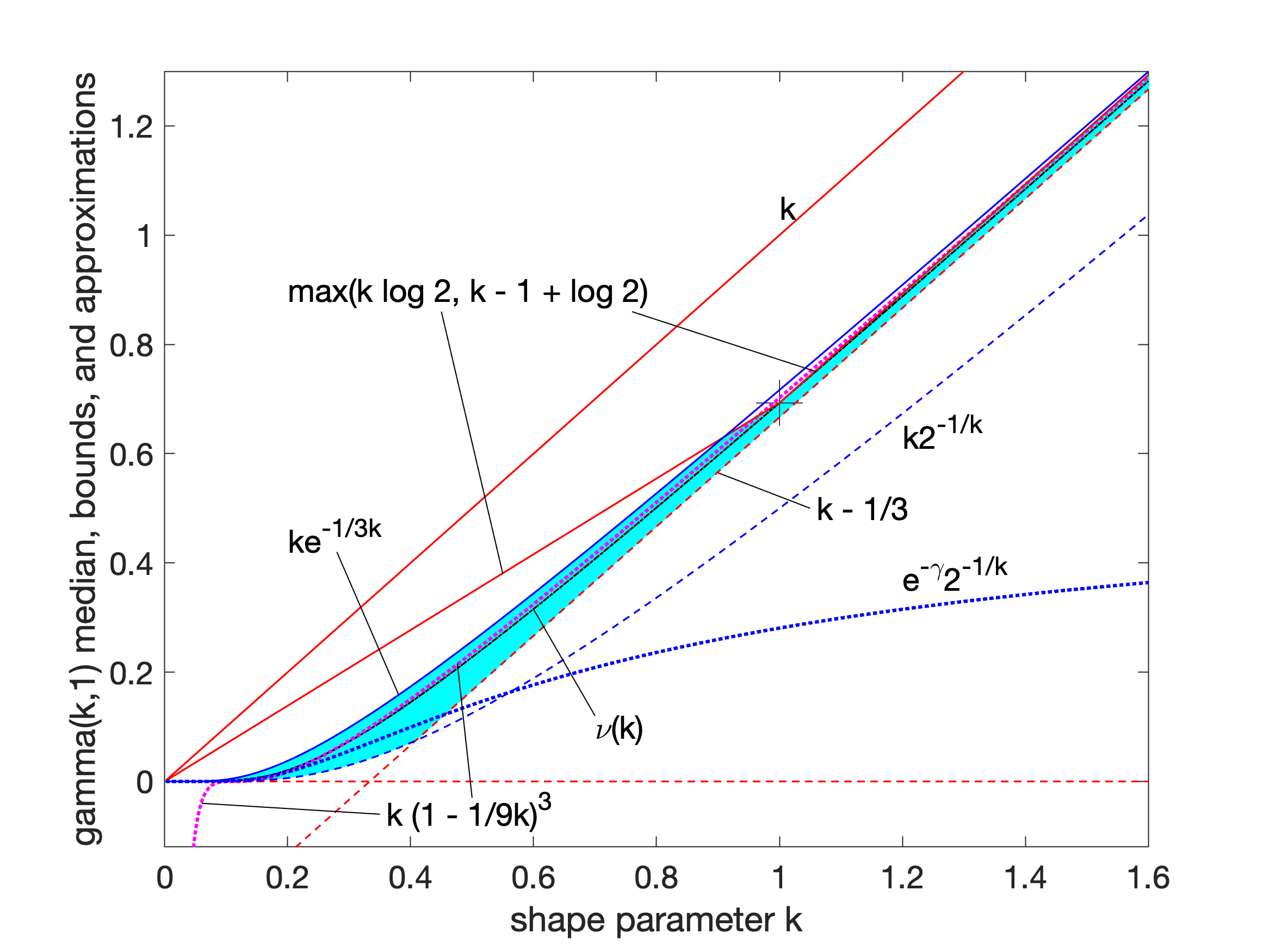
Gamma Distribution
In probability theory and statistics, the gamma distribution is a versatile two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-squared distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use: # With a shape parameter and a scale parameter # With a shape parameter \alpha and a rate parameter In each of these forms, both parameters are positive real numbers. The distribution has important applications in various fields, including econometrics, Bayesian statistics, and life testing. In econometrics, the (''α'', ''θ'') parameterization is common for modeling waiting times, such as the time until death, where it often takes the form of an Erlang distribution for integer ''α'' values. Bayesian statisticians prefer the (''α'',''λ'') parameterization, utilizing the gamma distribution as a conjugate prior for several inverse scale parameters, facilit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |