|
AFT Model
"Aft", in nautical terminology, is an adjective or adverb meaning towards the stern (rear) of the ship, aircraft or spacecraft, when the frame of reference is within the ship, headed at the fore. For example, "Able Seaman Smith; lie aft!" or "What's happening aft?". The corresponding adjective in distinguishing one feature of the vessel from another is "after". Its antonym is "forward". The corresponding preposition is "abaft". For example, the mizzenmast is abaft the mainmast. Its antonym is "before" or, in a more clumsy form, "forward of". The difference between "aft" and "stern" is that aft is the (on board) rearmost part of the vessel, while stern refers to the (offboard) rearmost part of the vessel. The stern is opposite the bow, the outside (offboard) of the front of the boat. The term derives from the Old English ''æftan'' (“behind”). See also * * Port and starboard Port and starboard are nautical terms for watercraft and aircraft, referring respectiv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Glossary Of Nautical Terms (A-L)
This glossary of nautical terms is an alphabetical listing of terms and expressions connected with ships, shipping, seamanship and navigation on water (mostly though not necessarily on the sea). Some remain current, while many date from the 17th to 19th centuries. The word nautical derives from the Latin ''nauticus'', from Greek ''nautikos'', from ''nautēs'': "sailor", from ''naus'': "ship". Further information on nautical terminology may also be found at Nautical metaphors in English, and additional military terms are listed in the Multiservice tactical brevity code article. Terms used in other fields associated with bodies of water can be found at Glossary of fishery terms, Glossary of underwater diving terminology, Glossary of rowing terms, and Glossary of meteorology This glossary of meteorology is a list of terms and concepts relevant to meteorology and atmospheric science, their sub-disciplines, and related fields. A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adjective
In linguistics, an adjective ( abbreviated ) is a word that generally modifies a noun or noun phrase or describes its referent. Its semantic role is to change information given by the noun. Traditionally, adjectives were considered one of the main parts of speech of the English language, although historically they were classed together with nouns. Nowadays, certain words that usually had been classified as adjectives, including ''the'', ''this'', ''my'', etc., typically are classed separately, as determiners. Here are some examples: * That's a funny idea. ( attributive) * That idea is funny. ( predicative) * * The good, the bad, and the funny. (substantive) Etymology ''Adjective'' comes from Latin ', a calque of grc, ἐπίθετον ὄνομα, epítheton ónoma, additional noun (whence also English ''epithet''). In the grammatical tradition of Latin and Greek, because adjectives were inflected for gender, number, and case like nouns (a process called declension), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adverb
An adverb is a word or an expression that generally modifies a verb, adjective, another adverb, determiner, clause, preposition, or sentence. Adverbs typically express manner, place, time, frequency, degree, level of certainty, etc., answering questions such as ''how'', ''in what way'', ''when'', ''where'', ''to what extent''. This is called the adverbial function and may be performed by single words (adverbs) or by multi-word adverbial phrases and adverbial clauses. Adverbs are traditionally regarded as one of the parts of speech. Modern linguists note that the term "adverb" has come to be used as a kind of "catch-all" category, used to classify words with various types of syntactic behavior, not necessarily having much in common except that they do not fit into any of the other available categories (noun, adjective, preposition, etc.) Functions The English word ''adverb'' derives (through French) from Latin ''adverbium'', from ''ad-'' ("to"), ''verbum'' ("word", "verb"), an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
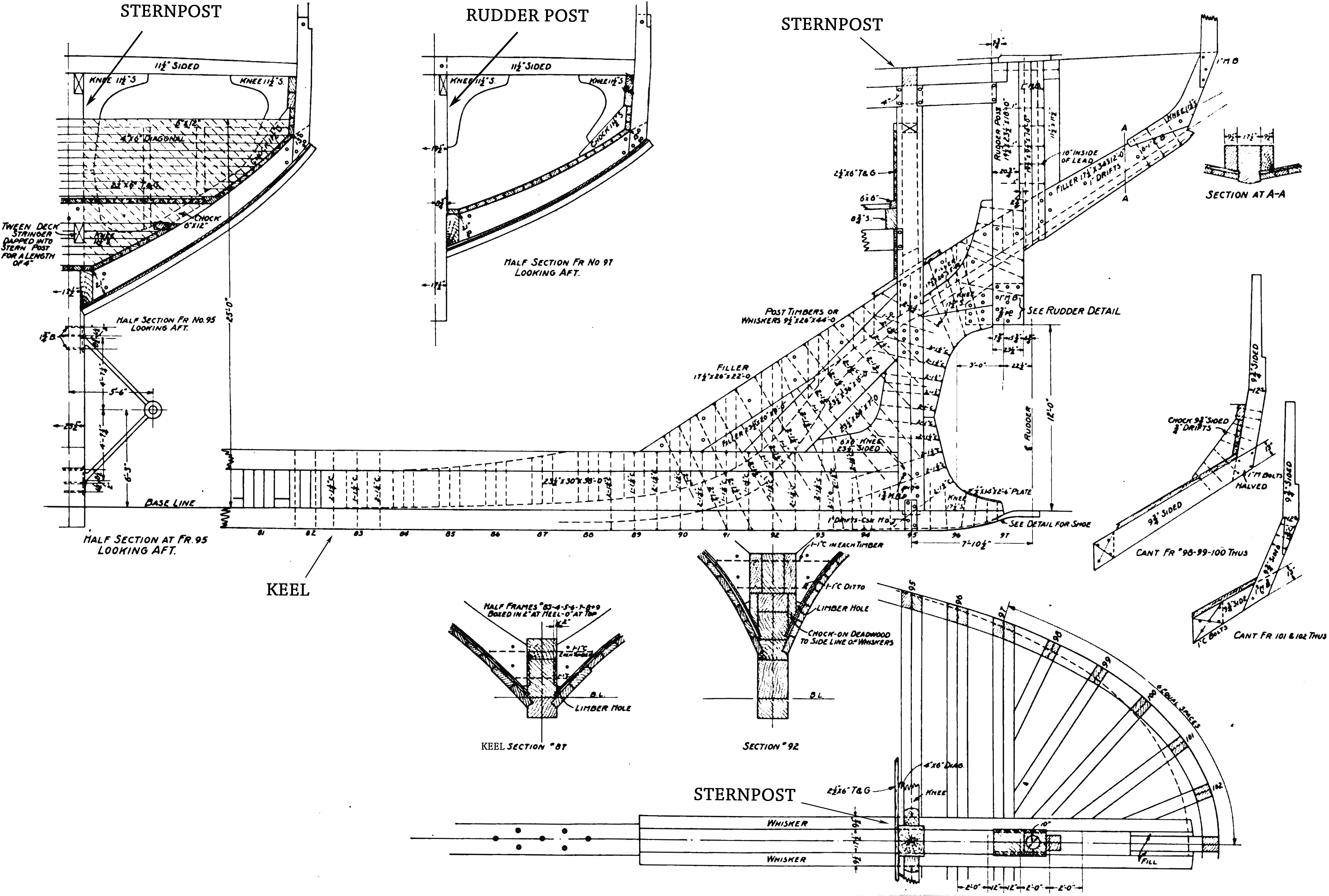
Stern
The stern is the back or aft-most part of a ship or boat, technically defined as the area built up over the sternpost, extending upwards from the counter rail to the taffrail. The stern lies opposite the bow, the foremost part of a ship. Originally, the term only referred to the aft port section of the ship, but eventually came to refer to the entire back of a vessel. The stern end of a ship is indicated with a white navigation light at night. Sterns on European and American wooden sailing ships began with two principal forms: the ''square'' or ''transom'' stern and the ''elliptical'', ''fantail'', or ''merchant'' stern, and were developed in that order. The hull sections of a sailing ship located before the stern were composed of a series of U-shaped rib-like frames set in a sloped or "cant" arrangement, with the last frame before the stern being called the ''fashion timber(s)'' or ''fashion piece(s)'', so called for "fashioning" the after part of the ship. This frame is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ship
A ship is a large watercraft that travels the world's oceans and other sufficiently deep waterways, carrying cargo or passengers, or in support of specialized missions, such as defense, research, and fishing. Ships are generally distinguished from boats, based on size, shape, load capacity, and purpose. Ships have supported exploration, trade, warfare, migration, colonization, and science. After the 15th century, new crops that had come from and to the Americas via the European seafarers significantly contributed to world population growth. Ship transport is responsible for the largest portion of world commerce. The word ''ship'' has meant, depending on the era and the context, either just a large vessel or specifically a ship-rigged sailing ship with three or more masts, each of which is square-rigged. As of 2016, there were more than 49,000 merchant ships, totaling almost 1.8 billion dead weight tons. Of these 28% were oil tankers, 43% were bulk carriers, and 1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aircraft
An aircraft is a vehicle that is able to fly by gaining support from the air. It counters the force of gravity by using either static lift or by using the dynamic lift of an airfoil, or in a few cases the downward thrust from jet engines. Common examples of aircraft include airplanes, helicopters, airships (including blimps), Glider (aircraft), gliders, Powered paragliding, paramotors, and hot air balloons. The human activity that surrounds aircraft is called ''aviation''. The science of aviation, including designing and building aircraft, is called ''aeronautics.'' Aircrew, Crewed aircraft are flown by an onboard Aircraft pilot, pilot, but unmanned aerial vehicles may be remotely controlled or self-controlled by onboard computers. Aircraft may be classified by different criteria, such as lift type, Powered aircraft#Methods of propulsion, aircraft propulsion, usage and others. History Flying model craft and stories of manned flight go back many centuries; however, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spacecraft
A spacecraft is a vehicle or machine designed to spaceflight, fly in outer space. A type of artificial satellite, spacecraft are used for a variety of purposes, including Telecommunications, communications, Earth observation satellite, Earth observation, Weather satellite, meteorology, navigation, space colonization, Planetary science, planetary exploration, and Space transport, transportation of Human spaceflight, humans and cargo spacecraft, cargo. All spacecraft except single-stage-to-orbit vehicles cannot get into space on their own, and require a launch vehicle (carrier rocket). On a sub-orbital spaceflight, a space vehicle enters outer space, space and then returns to the surface without having gained sufficient energy or velocity to make a full Earth orbit. For orbital spaceflights, spacecraft enter closed orbits around the Earth or around other Astronomical object, celestial bodies. Spacecraft used for human spaceflight carry people on board as crew or passengers from ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frame Of Reference
In physics and astronomy, a frame of reference (or reference frame) is an abstract coordinate system whose origin, orientation, and scale are specified by a set of reference points― geometric points whose position is identified both mathematically (with numerical coordinate values) and physically (signaled by conventional markers). For ''n'' dimensions, reference points are sufficient to fully define a reference frame. Using rectangular Cartesian coordinates, a reference frame may be defined with a reference point at the origin and a reference point at one unit distance along each of the ''n'' coordinate axes. In Einsteinian relativity, reference frames are used to specify the relationship between a moving observer and the phenomenon under observation. In this context, the term often becomes observational frame of reference (or observational reference frame), which implies that the observer is at rest in the frame, although not necessarily located at its origin. A rela ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bow (watercraft)
The bow () is the forward part of the hull of a ship or boat, the point that is usually most forward when the vessel is underway. The aft end of the boat is the stern. Prow may be used as a synonym for bow or it may mean the forward-most part of the bow above the waterline. Function A ship's bow should be designed to enable the hull to pass efficiently through the water. Bow shapes vary according to the speed of the boat, the seas or waterways being navigated, and the vessel's function. Where sea conditions are likely to promote pitching, it is useful if the bow provides reserve buoyancy; a flared bow (a raked stem with flared topsides) is ideal to reduce the amount of water shipped over the bow. Ideally, the bow should reduce the resistance and should be tall enough to prevent water from regularly washing over the top of it. Large commercial barges on inland waterways rarely meet big waves and may have remarkably little freeboard at the bow, whereas fast military vess ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Preposition
Prepositions and postpositions, together called adpositions (or broadly, in traditional grammar, simply prepositions), are a class of words used to express spatial or temporal relations (''in'', ''under'', ''towards'', ''before'') or mark various semantic roles (''of'', ''for''). A preposition or postposition typically combines with a noun phrase, this being called its complement, or sometimes object. A preposition comes before its complement; a postposition comes after its complement. English generally has prepositions rather than postpositions – words such as ''in'', ''under'' and ''of'' precede their objects, such as ''in England'', ''under the table'', ''of Jane'' – although there are a few exceptions including "ago" and "notwithstanding", as in "three days ago" and "financial limitations notwithstanding". Some languages that use a different word order have postpositions instead, or have both types. The phrase formed by a preposition or postposition together with its co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mizzenmast
The mast of a sailing vessel is a tall spar, or arrangement of spars, erected more or less vertically on the centre-line of a ship or boat. Its purposes include carrying sails, spars, and derricks, and giving necessary height to a navigation light, look-out position, signal yard, control position, radio aerial or signal lamp. Large ships have several masts, with the size and configuration depending on the style of ship. Nearly all sailing masts are guyed. Until the mid-19th century, all vessels' masts were made of wood formed from a single or several pieces of timber which typically consisted of the trunk of a conifer tree. From the 16th century, vessels were often built of a size requiring masts taller and thicker than could be made from single tree trunks. On these larger vessels, to achieve the required height, the masts were built from up to four sections (also called masts). From lowest to highest, these were called: lower, top, topgallant, and royal masts. Giving the lo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.png)


.jpg)