|
883 Symmetry
In geometry, the truncated order-6 octagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t. Uniform colorings A secondary construction t is called a truncated trioctaoctagonal tiling: : Symmetry The dual to this tiling represent the fundamental domains of 8,8,3)(*883) symmetry. There are 3 small index subgroup symmetries constructed from 8,8,3)by mirror removal and alternation. In these images fundamental domains are alternately colored black and white, and mirrors exist on the boundaries between colors. The symmetry can be doubled as 862 symmetry by adding a mirror bisecting the fundamental domain. Related polyhedra and tiling References * John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ''The Symmetries of Things'' 2008, (Chapter 19, The Hyperbolic Archimedean Tessellations) * See also *Tilings of regular polygons *List of uniform planar tilings This table shows the 11 convex uniform tilings (regular and semiregula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a '' geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
444444 Symmetry
In geometry, the order-8 hexagonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of . Uniform constructions There are four uniform constructions of this tiling, three of them as constructed by mirror removal from the ,6 kaleidoscope. Removing the mirror between the order 2 and 6 points, ,8,1+ gives 6,6,4) (*664). Removing the mirror between the order 8 and 6 points, ,1+,8 gives (*4232). Removing two mirrors as ,8* leaves remaining mirrors (*33333333). Symmetry This tiling represents a hyperbolic kaleidoscope of 4 mirrors meeting as edges of a square, with eight squares around every vertex. This symmetry by orbifold notation is called (*444444) with 6 order-4 mirror intersections. In Coxeter notation can be represented as ,6* removing two of three mirrors (passing through the square center) in the ,6symmetry. Related polyhedra and tiling See also *Uniform tilings in hyperbolic plane *List of regular polytopes References * John H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Truncated Tilings
Truncation is the term used for limiting the number of digits right of the decimal point by discarding the least significant ones. Truncation may also refer to: Mathematics * Truncation (statistics) refers to measurements which have been cut off at some value * Truncation (numerical analysis) refers to truncating an infinite sum by a finite one * Truncation (geometry) is the removal of one or more parts, as for example in truncated cube * Propositional truncation, a type former which truncates a type down to a mere proposition Computer science * Data truncation, an event that occurs when a file or other data is stored in a location too small to accommodate its entire length * Truncate (SQL), a command in the SQL data manipulation language to quickly remove all data from a table Biology * Truncate, a leaf shape * Truncated protein, a protein shortened by a mutation which specifically induces premature termination of messenger RNA translation Other uses * Cheque truncation, th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isogonal Tilings
Isogonal is a mathematical Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ... term which means "having similar angles". It occurs in several contexts: * Isogonal polygon, polyhedron, polytope or tiling. * Isogonal trajectory in curve theory. * Isogonal conjugate in triangle geometry. An Isogonal is also the name for a line connecting points at which the magnetic declination is the same. {{disambig Geometry ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Tilings
Hyperbolic is an adjective describing something that resembles or pertains to a hyperbola (a curve), to hyperbole (an overstatement or exaggeration), or to hyperbolic geometry. The following phenomena are described as ''hyperbolic'' because they manifest hyperbolas, not because something about them is exaggerated. * Hyperbolic angle, an unbounded variable referring to a hyperbola instead of a circle * Hyperbolic coordinates, location by geometric mean and hyperbolic angle in quadrant I * Hyperbolic distribution, a probability distribution characterized by the logarithm of the probability density function being a hyperbola * Hyperbolic equilibrium point, a fixed point that does not have any center manifolds * Hyperbolic function, an analog of an ordinary trigonometric or circular function * Hyperbolic geometric graph, a random network generated by connecting nearby points sprinkled in a hyperbolic space * Hyperbolic geometry, a non-Euclidean geometry * Hyperbolic group, a f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Regular Polytopes
This article lists the regular polytopes and regular polytope compounds in Euclidean, spherical and hyperbolic spaces. The Schläfli symbol describes every regular tessellation of an ''n''-sphere, Euclidean and hyperbolic spaces. A Schläfli symbol describing an ''n''-polytope equivalently describes a tessellation of an (''n'' − 1)-sphere. In addition, the symmetry of a regular polytope or tessellation is expressed as a Coxeter group, which Coxeter expressed identically to the Schläfli symbol, except delimiting by square brackets, a notation that is called Coxeter notation. Another related symbol is the Coxeter-Dynkin diagram which represents a symmetry group with no rings, and the represents regular polytope or tessellation with a ring on the first node. For example, the cube has Schläfli symbol , and with its octahedral symmetry, ,3or , it is represented by Coxeter diagram . The regular polytopes are grouped by dimension and subgrouped by convex, nonconve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Uniform Planar Tilings
This table shows the 11 convex uniform tilings (regular and semiregular) of the Euclidean plane, and their dual tilings. There are three regular and eight semiregular tilings in the plane. The semiregular tilings form new tilings from their duals, each made from one type of irregular face. John Conway calls these uniform duals ''Catalan tilings'', in parallel to the Catalan solid polyhedra. Uniform tilings are listed by their vertex configuration, the sequence of faces that exist on each vertex. For example ''4.8.8'' means one square and two octagons on a vertex. These 11 uniform tilings have 32 different '' uniform colorings''. A uniform coloring allows identical sided polygons at a vertex to be colored differently, while still maintaining vertex-uniformity and transformational congruence between vertices. (Note: Some of the tiling images shown below are ''not'' color-uniform) In addition to the 11 convex uniform tilings, there are also 14 known nonconvex tilings, using ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tilings Of Regular Polygons
Euclidean plane tilings by convex regular polygons have been widely used since antiquity. The first systematic mathematical treatment was that of Kepler in his '' Harmonices Mundi'' ( Latin: ''The Harmony of the World'', 1619). Notation of Euclidean tilings Euclidean tilings are usually named after Cundy & Rollett’s notation. This notation represents (i) the number of vertices, (ii) the number of polygons around each vertex (arranged clockwise) and (iii) the number of sides to each of those polygons. For example: 36; 36; 34.6, tells us there are 3 vertices with 2 different vertex types, so this tiling would be classed as a ‘3-uniform (2-vertex types)’ tiling. Broken down, 36; 36 (both of different transitivity class), or (36)2, tells us that there are 2 vertices (denoted by the superscript 2), each with 6 equilateral 3-sided polygons (triangles). With a final vertex 34.6, 4 more contiguous equilateral triangles and a single regular hexagon. However, this notation has ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John Horton Conway
John Horton Conway (26 December 1937 – 11 April 2020) was an English mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory. He also made contributions to many branches of recreational mathematics, most notably the invention of the cellular automaton called the Game of Life. Born and raised in Liverpool, Conway spent the first half of his career at the University of Cambridge before moving to the United States, where he held the John von Neumann Professorship at Princeton University for the rest of his career. On 11 April 2020, at age 82, he died of complications from COVID-19. Early life and education Conway was born on 26 December 1937 in Liverpool, the son of Cyril Horton Conway and Agnes Boyce. He became interested in mathematics at a very early age. By the time he was 11, his ambition was to become a mathematician. After leaving sixth form, he studied mathematics at Gonville and Caius College ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
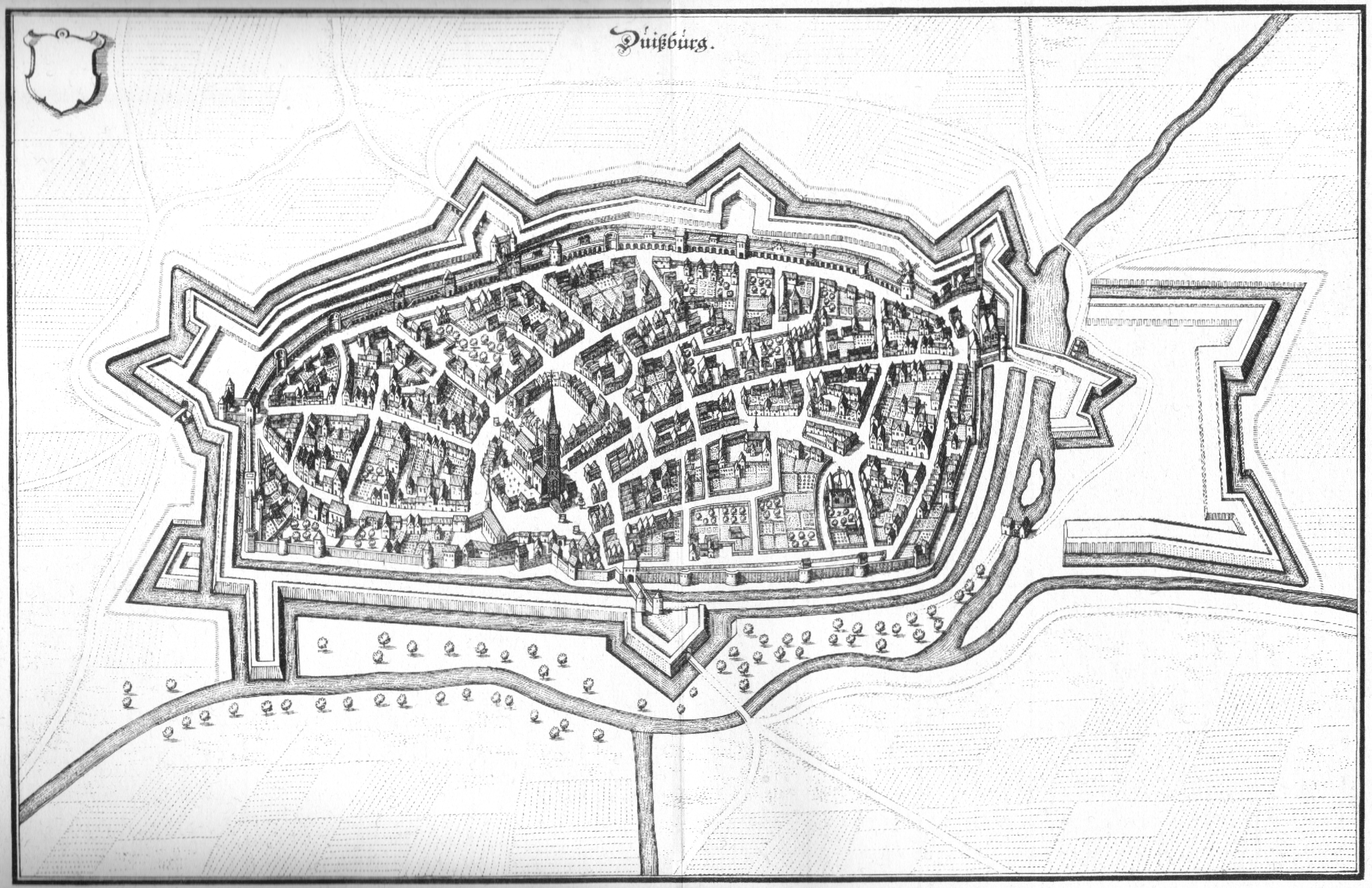
883 Symmetry Zaz
__NOTOC__ Year 883 ( DCCCLXXXIII) was a common year starting on Tuesday (link will display the full calendar) of the Julian calendar. Events By place Europe * Spring – Viking raiders ravage Flanders, and sack the abbey at Saint-Quentin. King Carloman II blocks their passage at Laviers, which had been on the banks of the Somme. Meanwhile, Vikings enter the Rhine, but are turned back by Henry of Franconia (possibly a margrave of Saxony). They over-winter at Duisburg. * King Charles the Fat travels to Nonantola (Northern Italy), where he meets Pope Marinus I. He receives complaints of Guy II of Spoleto, who is the official "protector" of Rome, and invades the Papal States. King Charles orders Guy to appear before a tribunal. * Guy II of Spoleto begins a revolt, and assembles an army supported with Arab auxiliaries. King Charles the Fat sends Berengar of Friuli with an expeditionary force to deprive him of Spoleto. An epidemic ravages Berengar's army, and forces ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |