|
833 Cents Scale
The 833 cents scale is a musical tuning and scale (music), scale proposed by Heinz Bohlen based on combination tones, an interval (music), interval of 833.09 cent (music), cents, and, coincidentally, the Fibonacci number, Fibonacci sequence.Bohlen, Heinz (last updated 2012).An 833 Cents Scale: An experiment on harmony, ''Huygens-Fokker.org''. The golden ratio is \varphi = \frac = 1.6180339887\ldots, which as a musical interval is 833.09 cents (). In the 833 cents scale this interval is taken as an alternative to the octave as the interval of octave-repeating scale, repetition,833 Cent Golden Scale (Bohlen) , ''Xenharmonic Wiki''. however the golden ratio is not regarded as an equivalence class (music), equivalent interval (notes 833.09 cents apart are not "the same" in the 833 cents scale the way notes 1200 cents ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Golden Ratio Line
Golden means made of, or relating to gold. Golden may also refer to: Places United Kingdom *Golden, in the parish of Probus, Cornwall *Golden Cap, Dorset *Golden Square, Soho, London *Golden Valley, a valley on the River Frome, Stroud#Golden Valley, River Frome in Gloucestershire *Golden Valley, Herefordshire United States *Golden, Colorado, a town West of Denver, county seat of Jefferson County *Golden, Idaho, an unincorporated community *Golden, Illinois, a village *Golden Township, Michigan *Golden, Mississippi, a village *Golden City, Missouri, a city *Golden, Missouri, an unincorporated community *Golden, Nebraska, ghost town in Burt County *Golden Township, Holt County, Nebraska *Golden, New Mexico, a sparsely populated ghost town *Golden, Oregon, an abandoned mining town *Golden, Texas, an unincorporated community *Golden, Utah, a ghost town *Golden, Marshall County, West Virginia, an unincorporated community Elsewhere *Golden, County Tipperary, Ireland, a village on the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limit (mathematics)
In mathematics, a limit is the value that a function (or sequence) approaches as the argument (or index) approaches some value. Limits of functions are essential to calculus and mathematical analysis, and are used to define continuity, derivatives, and integrals. The concept of a limit of a sequence is further generalized to the concept of a limit of a topological net, and is closely related to limit and direct limit in category theory. The limit inferior and limit superior provide generalizations of the concept of a limit which are particularly relevant when the limit at a point may not exist. Notation In formulas, a limit of a function is usually written as : \lim_ f(x) = L, and is read as "the limit of of as approaches equals ". This means that the value of the function can be made arbitrarily close to , by choosing sufficiently close to . Alternatively, the fact that a function approaches the limit as approaches is sometimes denoted by a right arrow (→ or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zipf's Law
Zipf's law (; ) is an empirical law stating that when a list of measured values is sorted in decreasing order, the value of the -th entry is often approximately inversely proportional to . The best known instance of Zipf's law applies to the frequency table of words in a text or corpus of natural language: \ \mathsf\ \propto\ \frac ~. It is usually found that the most common word occurs approximately twice as often as the next common one, three times as often as the third most common, and so on. For example, in the Brown Corpus of American English text, the word "''the''" is the most frequently occurring word, and by itself accounts for nearly 7% of all word occurrences (69,971 out of slightly over 1 million). True to Zipf's law, the second-place word "''of''" accounts for slightly over 3.5% of words (36,411 occurrences), followed by "''and''" (28,852). It is often used in the following form, called Zipf-Mandelbrot law: \ \mathsf\ \propto\ \frac\ where \ a\ a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kepler Triangle
A Kepler triangle is a special right triangle with edge lengths in geometric progression. The ratio of the progression is \sqrt\varphi where \varphi=(1+\sqrt)/2 is the golden ratio, and the progression can be written: or approximately . Squares on the edges of this triangle have areas in another geometric progression, 1:\varphi:\varphi^2. Alternative definitions of the same triangle characterize it in terms of the three Pythagorean means of two numbers, or via the inradius of isosceles triangles. This triangle is named after Johannes Kepler, but can be found in earlier sources. Although some sources claim that ancient Egyptian pyramids had proportions based on a Kepler triangle, most scholars believe that the golden ratio was not known to Egyptian mathematics and architecture. History The Kepler triangle is named after the German mathematician and astronomer Johannes Kepler (1571–1630), who wrote about this shape in a 1597 letter. Two concepts that can be used to analyze th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
36 Equal Temperament
''Sixth Tone'' () is a Chinese state-owned English-language online magazine published by Shanghai United Media Group. Name ''Sixth Tone'''s name relates to the number of tones in Mandarin Chinese, but also is stated to carry more metaphorical meaning as well. Mandarin Chinese has four active tones and a fifth dropped tone that has less prominence than the other four. Because of the language's five tones, the publication's name refers to an ideal of expanding beyond traditionally-reported items in Anglophone media, making it the "sixth tone". History The online magazine began publication on April 6, 2016, with an investment of US$4.5 million from the Shanghai United Media Group. It is a sister publication of ''The Paper''. Wei Xing was its first editor-in-chief until May 30, 2016, when he moved to create a start-up company and therefore no longer worked for the paper. Succeeding Wei, Zhang Jun became the new editor-in-chief that year. By 2018, Western media began to cite ''S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generated Collection
In music theory, a generated collection is a collection or scale formed by repeatedly adding a constant interval in integer notation, the generator, also known as an interval cycle, around the chromatic circle until a complete collection or scale is formed. All scales with the deep scale property can be generated by any interval coprime with the number of notes per octave. (Johnson, 2003, p. 83) The C major diatonic collection can be generated by adding a cycle of perfect fifths (C7) starting at F: F-C-G-D-A-E-B = C-D-E-F-G-A-B. Using integer notation and 12-tone equal temperament, the standard tuning of Western music: 5 + 7 = 0, 0 + 7 = 7, 7 + 7 = 2, 2 + 7 = 9, 9 + 7 = 4, 4 + 7 = 11. The C major scale could also be generated using cycle of perfect fourths (C5), as 12 minus any coprime of twelve is also coprime with twelve: 12 − 7&nbs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle Of Fifths
In music theory, the circle of fifths (sometimes also cycle of fifths) is a way of organizing pitches as a sequence of perfect fifths. Starting on a C, and using the standard system of tuning for Western music (12-tone equal temperament), the sequence is: C, G, D, A, E, B, F/G, C/D, G/A, D/E, A/B, F, and C. This order places the most closely related key signatures adjacent to one another. Twelve-tone equal temperament tuning divides each octave into twelve equivalent semitones, and the circle of fifths leads to a C seven octaves above the starting point. If the fifths are tuned with an exact frequency ratio of 3:2 (the system of tuning known as just intonation), this is not the case (the circle does not "close"). Definition The circle of fifths organizes pitches in a sequence of perfect fifths, generally shown as a circle with the pitches (and their corresponding keys) in clockwise order. It can be viewed in a counterclockwise direction as a circle of fourths. Harmonic progres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
833 Cents Scale Generator Circle W P5 And P4 Bnw 7
__NOTOC__ Year 833 ( DCCCXXXIII) was a common year starting on Wednesday of the Julian calendar. Events By place Byzantine Empire * Byzantine-Arab War: Emperor Theophilos signs an armistice for peace with the Abbasid Caliphate. He offers Caliph Al-Ma'mun 100,000 gold dinars, in return for 7,000 Byzantine prisoners.J. Norwich, ''Byzantine: The Apogee'', p. 47. Europe * June – Lothair I, eldest son of Emperor Louis the Pious, joins the rebellion of his brothers Pepin I and Louis the German, with the assistance of Archbishop Ebbo. Louis is forced to abdicate, on the plains of Rothfield (near Colmar). * Mojmir I, Moravian duke, expels Prince Pribina from his homeland (western part of modern Slovakia). He unifies Great Moravia and becomes the first known ruler of the Moravian Slavs, who founds the House of Mojmir (approximate date). * Galindo Aznárez I, Frankish count, usurps the Catalan counties ('' pagi'') of Pallars and Ribagorza, in the Spanish March (mod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heptatonic Scale
A heptatonic scale is a musical scale (music), scale that has seven pitch (music), pitches, or musical tone, tones, per octave. Examples include: * the #Diatonic scale, diatonic scale; including the major scale and its modes (notably the natural minor scale, or Aeolian mode) * the #Melodic minor scale, melodic minor scale, like the Aeolian mode but with raised 6th and 7th ascending * the #Harmonic minor scale, harmonic minor scale, like the Aeolian mode but with raised 7th * the harmonic major scale, like the major scale but with lowered 6th Indian classical theory postulates seventy-two seven-tone scale types, collectively called ''#Melakarta, melakarta'' or ''#Thaat, thaat'', whereas others postulate twelve or ten (depending on the theorist) seven-tone scale types. Several heptatonic scales in Western culture, Western, Roman, Spanish, Hungarian, and Greek music can be analyzed as juxtapositions of Tetrachord#Romantic era, tetrachords.Dupré, Marcel (1962). ''Cours Complet d'Impr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetric Scale
In music, a music scale can have certain symmetries, namely translational symmetry and inversional or mirror symmetry. The most prominent examples are scales which equally divides the octave. The concept and term appears to have been introduced by Joseph Schillinger and further developed by Nicolas Slonimsky as part of his famous ''Thesaurus of Scales and Melodic Patterns''. In twelve-tone equal temperament, the octave can only be equally divided into two, three, four, six, or twelve parts, which consequently may be filled in by adding the same exact interval or sequence of intervals to each resulting note (called "interpolation of notes"). This leads to scales with translational symmetry which include the octatonic scale (also known as the ''symmetric diminished'' scale; its mirror image is known as the ''inverse symmetric diminished'' scale) and the two-semitone tritone scale: As explained above, both are composed of repeating sub-units within an octave. This property allows ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Irrational Number
In mathematics, the irrational numbers are all the real numbers that are not rational numbers. That is, irrational numbers cannot be expressed as the ratio of two integers. When the ratio of lengths of two line segments is an irrational number, the line segments are also described as being '' incommensurable'', meaning that they share no "measure" in common, that is, there is no length ("the measure"), no matter how short, that could be used to express the lengths of both of the two given segments as integer multiples of itself. Among irrational numbers are the ratio of a circle's circumference to its diameter, Euler's number ''e'', the golden ratio ''φ'', and the square root of two. In fact, all square roots of natural numbers, other than of perfect squares, are irrational. Like all real numbers, irrational numbers can be expressed in positional notation, notably as a decimal number. In the case of irrational numbers, the decimal expansion does not terminate, nor end ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
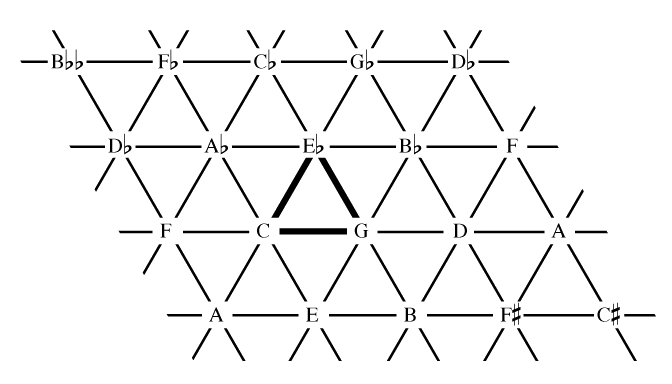
Lattice (music)
In musical tuning, a lattice "is a way of modeling the tuning relationships of a just intonation system. It is an array of points in a periodic multidimensional pattern. Each point on the lattice corresponds to a ratio (i.e., a pitch, or an interval with respect to some other point on the lattice). The lattice can be two-, three-, or ''n''-dimensional, with each dimension corresponding to a different prime-number partial ." When listed in a spreadsheet a lattice may be referred to as a tuning table. The points in a lattice represent pitch classes (or pitches if octaves are represented), and the connectors in a lattice represent the intervals between them. The connecting lines in a lattice display intervals as vectors, so that a line of the same length and angle always has the same intervalic relationship between the points it connects, no matter where it occurs in the lattice. Repeatedly adding the same vector (repeatedly stacking the same interval) moves you further in the sam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |