Kepler triangle

A Kepler triangle is a special right triangle with edge lengths in geometric progression. The ratio of the progression is $\sqrt\varphi$ where $\varphi=(1+\sqrt)/2$ is the golden ratio, and the progression can be written: or approximately . Squares on the edges of this triangle have areas in another geometric progression, $1:\varphi:\varphi^2$. Alternative definitions of the same triangle characterize it in terms of the three Pythagorean means of two numbers, or via the inradius of isosceles triangles.

This triangle is named after Johannes Kepler, but can be found in earlier sources. Although some sources claim that ancient Egyptian pyramids had proportions based on a Kepler triangle, most scholars believe that the golden ratio was not known to Egyptian mathematics and architecture.

History

The Kepler triangle is named after the German mathematician and astronomer Johannes Kepler (1571–1630), who wrote about this shape in a 1597 letter. Two concepts that can be used to analyze this triangle, the Pythagorean theorem and the golden ratio, were both of interest to Kepler, as he wrote elsewhere:

However, Kepler was not the first to describe this triangle. Kepler himself credited it to "a music professor named Magirus". The same triangle appears earlier in a book of Arabic mathematics, the ''Liber mensurationum'' of Abû Bekr, known from a 12th-century translation by Gerard of Cremona into Latin, and in the ' of Fibonacci (published in 1220–1221), who defined it in a similar way to Kepler. A little earlier than Kepler, Pedro Nunes wrote about it in 1567, and it is "likely to have been widespread in late medieval and Renaissance manuscript traditions". It has also been independently rediscovered several times, later than Kepler.

According to some authors, a "golden pyramid" with a doubled Kepler triangle as its cross-section accurately describes the design of Egyptian pyramids such as the Great Pyramid of Giza; one source of this theory is a 19th-century misreading of Herodotus by pyramidologist John Taylor. Many other theories of proportion have been proposed for the same pyramid, unrelated to the Kepler triangle. Because these different theories are very similar in the numeric values they obtain, and because of inaccuracies in measurement, in part caused by the destruction of the outer surface of the pyramid, such theories are difficult to resolve based purely on physical evidence. The match in proportions to the Kepler triangle may well be a numerical coincidence: according to scholars who have investigated this relationship, the ancient Egyptians most likely did not know about or use the golden ratio in their mathematics or architecture. Instead, the proportions of the pyramid can be adequately explained using integer ratios, based on a right triangle with sides

The name "Kepler triangle" for this shape was used by Roger Herz-Fischler, based on Kepler's 1597 letter, as early as 1979. Another name for the same triangle, used by Matila Ghyka in his 1946 book on the golden ratio, ''The Geometry of Art and Life'', is the "triangle of Price", after pyramidologist W. A. Price.

Definitions

The Kepler triangle is uniquely defined by the properties of being a right triangle and of having its side lengths in geometric progression,
or equivalently having the squares on its sides in geometric progression. The ratio of the progression of side lengths is where $\varphi=(1+\sqrt)/2$ is the golden ratio, and the progression can be written: or approximately 1 : 1.272 : 1.618. Squares on the edges of this triangle have areas in another geometric progression, $1:\varphi:\varphi^2$.
The fact that the triangle with these proportions is a right triangle follows from the fact that, for squared edge lengths with these proportions,
the defining polynomial of the golden ratio is the same as the formula given by the Pythagorean theorem for the squared edge lengths of a right triangle:
$\varphi^2 = \varphi + 1.$
Because this equation is true for the golden ratio, these three lengths obey the Pythagorean theorem, and form a right triangle. Conversely, in any right triangle whose squared edge lengths are in geometric progression with any ratio $\rho$, the Pythagorean theorem implies that this ratio obeys the identity $\rho^2=\rho+1$. Therefore, the ratio must be the unique positive solution to this equation, the golden ratio, and the triangle must be a Kepler triangle.

The three edge lengths $1$, $\sqrt\varphi$ and $\varphi$ are the harmonic mean, geometric mean, and arithmetic mean, respectively, of the two numbers These three ways of combining two numbers were all studied in ancient Greek mathematics, and are called the Pythagorean means. Conversely, this can be taken as an alternative definition of the Kepler triangle: it is a right triangle whose edge lengths are the three Pythagorean means of some two numbers. The only triangles for which this is true are the Kepler triangles.

A third, equivalent way of defining this triangle comes from a problem of maximizing the inradius of isosceles triangles.
Among all isosceles triangles with a fixed choice of the length of the two equal sides but with a variable base length, the one with the largest inradius is formed from two copies of the Kepler triangle, reflected across their longer sides from each other. Therefore, the Kepler triangle can be defined as the right triangle that, among all right triangles with the same hypotenuse, forms with its reflection the isosceles triangle of maximum inradius. The same reflection also forms an isosceles triangle that, for a given perimeter, contains the largest possible semicircle.

Properties

If the short side of a Kepler triangle has length $s$, the other sides will have lengths $s\sqrt\varphi$ and $s\varphi$. The area can be calculated by the standard formula for the area of right triangles (half the product of the two short sides) as $\tfrac\sqrt\varphi$. The cosine of the larger of the two non-right angles is the ratio of the adjacent side (the shorter of the two sides) to the hypotenuse, $\varphi$, from which it follows that the two non-right angles are
$\theta=\sin^\frac\approx 38.1727^\circ$
and
$\theta=\cos^\frac\approx 51.8273^\circ.$

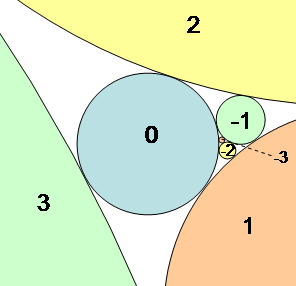
Jerzy Kocik has observed that the larger of these two angles is also the angle formed by the centers of triples of consecutive circles in Coxeter's loxodromic sequence of tangent circles.

See also

* Automedian triangle, a triangle whose squared side lengths form an arithmetic progression, including the right triangle with side lengths $1:\sqrt2:\sqrt3$
* Golden triangle, an isosceles triangle whose ratio of base to side length is the golden ratio.

References

{{Johannes Kepler

Types of triangles
Golden ratio
Johannes Kepler
Eponymous geometric shapes