|
236 (number)
236 (two hundred ndthirty-six) is the natural number following 235 and preceding 237. 236 is a happy number. In mathematics * There are 236 different connected graphs with eight vertices and nine edges, and 236 different degree sequence In graph theory, the degree (or valency) of a vertex of a graph is the number of edges that are incident to the vertex; in a multigraph, a loop contributes 2 to a vertex's degree, for the two ends of the edge. The degree of a vertex v is deno ...s of six-vertex graphs. In other fields There are 236 different phylogenetic trees representing the history of evolutionary divergences among five species. References Integers {{Num-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Number
In mathematics, the natural numbers are those numbers used for counting (as in "there are ''six'' coins on the table") and ordering (as in "this is the ''third'' largest city in the country"). Numbers used for counting are called '' cardinal numbers'', and numbers used for ordering are called '' ordinal numbers''. Natural numbers are sometimes used as labels, known as ''nominal numbers'', having none of the properties of numbers in a mathematical sense (e.g. sports jersey numbers). Some definitions, including the standard ISO 80000-2, begin the natural numbers with , corresponding to the non-negative integers , whereas others start with , corresponding to the positive integers Texts that exclude zero from the natural numbers sometimes refer to the natural numbers together with zero as the whole numbers, while in other writings, that term is used instead for the integers (including negative integers). The natural numbers form a set. Many other number sets are built by succ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
235 (number)
235 (two hundred ndthirty-five) is the integer following 234 and preceding 236. In mathematics 235 is: *a semiprime. *a heptagonal number. *a centered triangular number. *therefore a figurate number in two ways. *palindromic in bases 4 (32234), 7 (4547), 8 (3538), 13 (15113), and 46 (5546). *a Harshad number in bases 6, 47, 48, 95, 116, 189 and 231. *a Smarandache–Wellin number Also: *There are 235 different trees with 11 unlabeled nodes. *If an equilateral triangle is subdivided into smaller equilateral triangles whose side length is 1/9 as small, the resulting "matchstick arrangement" will have exactly 235 different equilateral triangles of varying sizes in it. In science *U-235 is the fissile isotope of uranium used in the first atomic bombs. See also *List of highways numbered 235 *235 film, 35 mm film in daylight-loading spools *Superscope 235, a motion picture film format *2.35 to 1 widescreen aspect ratio in anamorphic format Anamorphic format is the cinema ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
237 (number)
237 (two hundred ndthirty-seven) is the natural number following 236 and preceding 238. 237 is a lucky number, and one of the numbers in Aronson's sequence. The 237th square pyramidal number In mathematics, a pyramid number, or square pyramidal number, is a natural number that counts the number of stacked spheres in a pyramid with a square base. The study of these numbers goes back to Archimedes and Fibonacci. They are part of a broa ..., 4465475, is also a sum of two smaller square pyramidal numbers. There are only four smaller numbers (55, 70, 147, and 226) with the same property. References Integers {{Num-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Happy Number
In number theory, a happy number is a number which eventually reaches 1 when replaced by the sum of the square of each digit. For instance, 13 is a happy number because 1^2+3^2=10, and 1^2+0^2=1. On the other hand, 4 is not a happy number because the sequence starting with 4^2=16 and 1^2+6^2=37 eventually reaches 2^2+0^2=4, the number that started the sequence, and so the process continues in an infinite cycle without ever reaching 1. A number which is not happy is called sad or unhappy. More generally, a b-happy number is a natural number in a given number base b that eventually reaches 1 when iterated over the perfect digital invariant function for p = 2. The origin of happy numbers is not clear. Happy numbers were brought to the attention of Reg Allenby (a British author and senior lecturer in pure mathematics at Leeds University) by his daughter, who had learned of them at school. However, they "may have originated in Russia" . Happy numbers and perfect digital invaria ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Connected Graph
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements (nodes or edges) that need to be removed to separate the remaining nodes into two or more isolated subgraphs. It is closely related to the theory of network flow problems. The connectivity of a graph is an important measure of its resilience as a network. Connected vertices and graphs In an undirected graph , two '' vertices'' and are called connected if contains a path from to . Otherwise, they are called disconnected. If the two vertices are additionally connected by a path of length , i.e. by a single edge, the vertices are called adjacent. A graph is said to be connected if every pair of vertices in the graph is connected. This means that there is a path between every pair of vertices. An undirected graph that is not connected is called disconnected. An undirected graph ''G'' is therefore disconnected if there exist two vertic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degree Sequence
In graph theory, the degree (or valency) of a vertex of a graph is the number of edges that are incident to the vertex; in a multigraph, a loop contributes 2 to a vertex's degree, for the two ends of the edge. The degree of a vertex v is denoted \deg(v) or \deg v. The maximum degree of a graph G, denoted by \Delta(G), and the minimum degree of a graph, denoted by \delta(G), are the maximum and minimum of its vertices' degrees. In the multigraph shown on the right, the maximum degree is 5 and the minimum degree is 0. In a regular graph, every vertex has the same degree, and so we can speak of ''the'' degree of the graph. A complete graph (denoted K_n, where n is the number of vertices in the graph) is a special kind of regular graph where all vertices have the maximum possible degree, n-1. In a signed graph, the number of positive edges connected to the vertex v is called positive deg(v) and the number of connected negative edges is entitled negative deg(v). Handshaking lemma T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
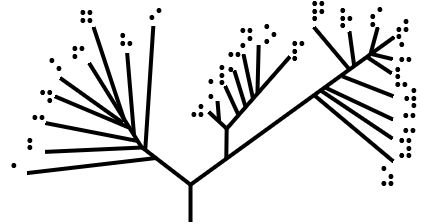
Phylogenetic Tree
A phylogenetic tree (also phylogeny or evolutionary tree Felsenstein J. (2004). ''Inferring Phylogenies'' Sinauer Associates: Sunderland, MA.) is a branching diagram or a tree showing the evolutionary relationships among various biological species or other entities based upon similarities and differences in their physical or genetic characteristics. All life on Earth is part of a single phylogenetic tree, indicating common ancestry. In a ''rooted'' phylogenetic tree, each node with descendants represents the inferred most recent common ancestor of those descendants, and the edge lengths in some trees may be interpreted as time estimates. Each node is called a taxonomic unit. Internal nodes are generally called hypothetical taxonomic units, as they cannot be directly observed. Trees are useful in fields of biology such as bioinformatics, systematics, and phylogenetics. ''Unrooted'' trees illustrate only the relatedness of the leaf nodes and do not require the ancestral root ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |