|
‚ôØP-completeness Of 01-permanent
The #P-completeness of 01-permanent, sometimes known as Valiant's theorem,Christos H. Papadimitriou. ''Computational Complexity.'' Addison-Wesley, 1994. . Page 443 is a mathematical proof about the permanent of matrices, considered a seminal result in computational complexity theory. In a 1979 scholarly paper, Leslie Valiant proved that the computational problem of computing the permanent of a matrix is #P-hard, even if the matrix is restricted to have entries that are all 0 or 1. In this restricted case, computing the permanent is even #P-complete, because it corresponds to the #P problem of counting the number of permutation matrices one can get by changing ones into zeroes. Valiant's 1979 paper also introduced #P as a complexity class. Valiant's definition of completeness, and his proof of completeness of 01-permanent, both used polynomial-time Turing reductions. In this kind of reduction, a single hard instance of some other problem in #P is reduced to computing the p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Christos Papadimitriou
Christos Charilaos Papadimitriou ( el, ŒßœÅŒÆœÉœÑŒøœÇ ŒßŒ±œÅŒØŒªŒ±ŒøœÇ "ŒßœÅŒØœÉœÑŒøœÇ" ŒÝŒ±œÄŒ±Œ¥Œ∑ŒºŒ∑œÑœÅŒØŒøœÖ; born August 16, 1949) is a Greek theoretical computer scientist and the Donovan Family Professor of Computer Science at Columbia University. Education Papadimitriou studied at the National Technical University of Athens, where in 1972 he received his Bachelor of Arts degree in electrical engineering. He then pursued graduate studies at Princeton University, where he received his Ph.D. in electrical engineering and computer science in 1976 after completing a doctoral dissertation titled "The complexity of combinatorial optimization problems." Career Papadimitriou has taught at Harvard, MIT, the National Technical University of Athens, Stanford, UCSD, University of California, Berkeley and is currently the Donovan Family Professor of Computer Science at Columbia University. Papadimitriou co-authored a paper on pancake sorting with Bill Gates, then a Harvard under ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Turing Reduction
In computability theory, a Turing reduction from a decision problem A to a decision problem B is an oracle machine which decides problem A given an oracle for B (Rogers 1967, Soare 1987). It can be understood as an algorithm that could be used to solve A if it had available to it a subroutine for solving ''B''. The concept can be analogously applied to function problems. If a Turing reduction from A to B exists, then every algorithm for B can be used to produce an algorithm for A, by inserting the algorithm for B at each place where the oracle machine computing A queries the oracle for B. However, because the oracle machine may query the oracle a large number of times, the resulting algorithm may require more time asymptotically than either the algorithm for B or the oracle machine computing A. A Turing reduction in which the oracle machine runs in polynomial time is known as a Cook reduction. The first formal definition of relative computability, then called relative reducibili ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Seinosuke Toda
is a computer scientist working at the Nihon University in Tokyo. Toda earned his Ph.D. from the Tokyo Institute of Technology in 1992, under the supervision of Kojiro Kobayashi. He was a recipient of the 1998 Gödel Prize for proving Toda's theorem in computational complexity theory, which states that every problem in the polynomial hierarchy In computational complexity theory, the polynomial hierarchy (sometimes called the polynomial-time hierarchy) is a hierarchy of complexity classes that generalize the classes NP and co-NP. Each class in the hierarchy is contained within PSPACE. ... has a polynomial-time Turing reduction to a counting problem. Notes Japanese computer scientists 20th-century Japanese mathematicians 21st-century Japanese mathematicians Theoretical computer scientists Gödel Prize laureates 1959 births Living people Academic staff of Nihon University {{Compu-scientist-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial Hierarchy
In computational complexity theory, the polynomial hierarchy (sometimes called the polynomial-time hierarchy) is a hierarchy of complexity classes that generalize the classes NP and co-NP. Each class in the hierarchy is contained within PSPACE. The hierarchy can be defined using oracle machines or alternating Turing machines. It is a resource-bounded counterpart to the arithmetical hierarchy and analytical hierarchy from mathematical logic. The union of the classes in the hierarchy is denoted PH. Classes within the hierarchy have complete problems (with respect to polynomial-time reductions) which ask if quantified Boolean formulae hold, for formulae with restrictions on the quantifier order. It is known that equality between classes on the same level or consecutive levels in the hierarchy would imply a "collapse" of the hierarchy to that level. Definitions There are multiple equivalent definitions of the classes of the polynomial hierarchy. Oracle definition For the or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Toda's Theorem
Toda's theorem is a result in computational complexity theory that was proven by Seinosuke Toda in his paper "PP is as Hard as the Polynomial-Time Hierarchy" and was given the 1998 Gödel Prize. Statement The theorem states that the entire polynomial hierarchy PH is contained in PPP; this implies a closely related statement, that PH is contained in P#P. Definitions #P is the problem of exactly counting the number of solutions to a polynomially-verifiable question (that is, to a question in NP), while loosely speaking, PP is the problem of giving an answer that is correct more than half the time. The class P#P consists of all the problems that can be solved in polynomial time if you have access to instantaneous answers to any counting problem in #P (polynomial time relative to a #P oracle). Thus Toda's theorem implies that for any problem in the polynomial hierarchy there is a deterministic polynomial-time Turing reduction to a counting problem. An analogous result in the c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dexter Kozen
Dexter Campbell Kozen (born December 20, 1951) is an American theoretical computer scientist. He is Joseph Newton Pew, Jr. Professor in Engineering at Cornell University. He received his B.A. from Dartmouth College in 1974 and his PhD in computer science in 1977 from Cornell University, where he was advised by Juris Hartmanis. He advised numerous Ph.D. students. He is a Fellow of the Association for Computing Machinery, a Guggenheim Fellow, and has received an Outstanding Innovation Award from IBM Corporation. He has also been named Faculty of the Year by the Association of Computer Science Undergraduates at Cornell. Dexter Kozen was one of the first professors to receive the honor of a professorship at The Radboud Excellence Initiative at Radboud University Nijmegen in the Netherlands. He is known for his work at the intersection of logic and complexity. He is one of the fathers of dynamic logic and developed the version of the modal μ-calculus most used today. Moreover, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adjacency Matrix
In graph theory and computer science, an adjacency matrix is a square matrix used to represent a finite graph. The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph. In the special case of a finite simple graph, the adjacency matrix is a (0,1)-matrix with zeros on its diagonal. If the graph is undirected (i.e. all of its edges are bidirectional), the adjacency matrix is symmetric. The relationship between a graph and the eigenvalues and eigenvectors of its adjacency matrix is studied in spectral graph theory. The adjacency matrix of a graph should be distinguished from its incidence matrix, a different matrix representation whose elements indicate whether vertex–edge pairs are incident or not, and its degree matrix, which contains information about the degree of each vertex. Definition For a simple graph with vertex set , the adjacency matrix is a square matrix such that its element is one when there is an edge from vertex to vert ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Richard Karp
Richard Manning Karp (born January 3, 1935) is an American computer scientist and computational theorist at the University of California, Berkeley. He is most notable for his research in the theory of algorithms, for which he received a Turing Award in 1985, The Benjamin Franklin Medal in Computer and Cognitive Science in 2004, and the Kyoto Prize in 2008. Karp was elected a member of the National Academy of Engineering (1992) for major contributions to the theory and application of NP-completeness, constructing efficient combinatorial algorithms, and applying probabilistic methods in computer science. Biography Born to parents Abraham and Rose Karp in Boston, Massachusetts, Karp has three younger siblings: Robert, David, and Carolyn. His family was Jewish,The Power and Limit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John Hopcroft
John Edward Hopcroft (born October 7, 1939) is an American theoretical computer scientist. His textbooks on theory of computation (also known as the Cinderella book) and data structures are regarded as standards in their fields. He is the IBM Professor of Engineering and Applied Mathematics in Computer Science at Cornell University, Co-Director of the Center on Frontiers of Computing Studies at Peking University, and the Director of the John Hopcroft Center for Computer Science at Shanghai Jiao Tong University. Education He received his bachelor's degree from Seattle University in 1961. He received his master's degree and Ph.D. from Stanford University in 1962 and 1964, respectively. He worked for three years at Princeton University and since then has been at Cornell University. Hopcroft is the grandson of Jacob Nist, founder of the Seattle-Tacoma Box Company. Career In addition to his research work, he is well known for his books on algorithms and formal languages coautho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
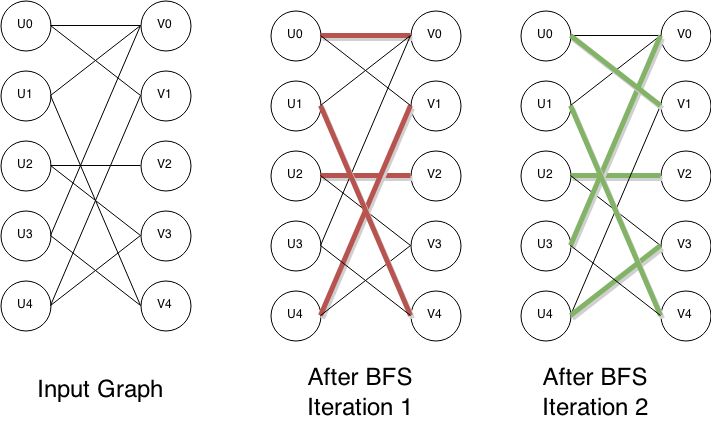
Hopcroft–Karp Algorithm
In computer science, the Hopcroft–Karp algorithm (sometimes more accurately called the Hopcroft–Karp–Karzanov algorithm) is an algorithm that takes a bipartite graph as input and produces a maximum cardinality matching as output – a set of as many edges as possible with the property that no two edges share an endpoint. It runs in O(, E, \sqrt) time in the worst case, where E is set of edges in the graph, V is set of vertices of the graph, and it is assumed that , E, =\Omega(, V, ). In the case of dense graphs the time bound becomes O(, V, ^), and for sparse random graphs it runs in time O(, E, \log , V, ) with high probability. The algorithm was discovered by and independently by . As in previous methods for matching such as the Hungarian algorithm and the work of , the Hopcroft–Karp algorithm repeatedly increases the size of a partial matching by finding ''augmenting paths''. These paths are sequences of edges of the graph, which alternate between edges in the matchi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bipartite Graph
In the mathematical field of graph theory, a bipartite graph (or bigraph) is a graph whose vertices can be divided into two disjoint and independent sets U and V, that is every edge connects a vertex in U to one in V. Vertex sets U and V are usually called the ''parts'' of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles. The two sets U and V may be thought of as a coloring of the graph with two colors: if one colors all nodes in U blue, and all nodes in V red, each edge has endpoints of differing colors, as is required in the graph coloring problem.. In contrast, such a coloring is impossible in the case of a non-bipartite graph, such as a triangle: after one node is colored blue and another red, the third vertex of the triangle is connected to vertices of both colors, preventing it from being assigned either color. One often writes G=(U,V,E) to denote a bipartite graph whose partition has the parts U and V, with E denotin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |