|
Łojasiewicz Inequality
In real algebraic geometry, the ┼üojasiewicz inequality, named after Stanis┼éaw ┼üojasiewicz, gives an upper bound for the distance of a point to the nearest zero of a given real analytic function. Specifically, let ŲÆ : ''U'' ŌåÆ R be a real analytic function on an open set ''U'' in R''n'', and let ''Z'' be the zero locus of ŲÆ. Assume that ''Z'' is not empty. Then for any compact set ''K'' in ''U'', there exist positive constants ╬▒ and ''C'' such that, for all ''x'' in ''K'' :\operatorname(x,Z)^\alpha \le C, f(x), . Here, \alpha can be small. The following form of this inequality is often seen in more analytic contexts: with the same assumptions on ''f'', for every ''p'' Ōłł ''U'' there is a possibly smaller open neighborhood ''W'' of ''p'' and constants ╬Ė Ōłł (0,1) and ''c'' > 0 such that :, f(x)-f(p), ^\theta\le c, \nabla f(x), . Polyak inequality A special case of the ┼üojasiewicz inequality, due to , is comm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Algebraic Geometry
In mathematics, real algebraic geometry is the sub-branch of algebraic geometry studying real algebraic sets, i.e. real-number solutions to algebraic equations with real-number coefficients, and mappings between them (in particular real polynomial mappings). Semialgebraic geometry is the study of semialgebraic sets, i.e. real-number solutions to algebraic inequalities with-real number coefficients, and mappings between them. The most natural mappings between semialgebraic sets are semialgebraic mappings, i.e., mappings whose graphs are semialgebraic sets. Terminology Nowadays the words 'semialgebraic geometry' and 'real algebraic geometry' are used as synonyms, because real algebraic sets cannot be studied seriously without the use of semialgebraic sets. For example, a projection of a real algebraic set along a coordinate axis need not be a real algebraic set, but it is always a semialgebraic set: this is the TarskiŌĆōSeidenberg theorem. Related fields are o-minimal theory ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Invex Function
In vector calculus, an invex function is a differentiable function f from \mathbb^n to \mathbb for which there exists a vector valued function \eta such that :f(x) - f(u) \geq \eta(x, u) \cdot \nabla f(u), \, for all ''x'' and ''u''. Invex functions were introduced by Hanson as a generalization of convex functions. Ben-Israel and Mond provided a simple proof that a function is invex if and only if every stationary point is a global minimum, a theorem first stated by Craven and Glover. Hanson also showed that if the objective and the constraints of an optimization problem are invex with respect to the same function \eta(x,u) , then the KarushŌĆōKuhnŌĆōTucker conditions are sufficient for a global minimum. Type I invex functions A slight generalization of invex functions called Type I invex functions are the most general class of functions for which the KarushŌĆōKuhnŌĆōTucker conditions are necessary and sufficient for a global minimum. Consider a mathematical program of the fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inequalities (mathematics)
Inequality may refer to: * Inequality (mathematics), a relation between two quantities when they are different. * Economic inequality, difference in economic well-being between population groups ** Income inequality, an unequal distribution of income ** Wealth inequality, an unequal distribution of wealth ** Spatial inequality, the unequal distribution of income and resources across geographical regions ** International inequality, economic differences between countries * Social inequality, unequal opportunities and rewards for different social positions or statuses within a group ** Gender inequality, unequal treatment or perceptions due to gender ** Racial inequality, social distinctions between racial and ethnic groups within a society * Health inequality, differences in the quality of health and healthcare across populations * Educational inequality, the unequal distribution of academic resources * Environmental inequality, unequal environmental harms between differe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transactions Of The American Mathematical Society
The ''Transactions of the American Mathematical Society'' is a monthly peer-reviewed scientific journal of pure and applied mathematics published by the American Mathematical Society. It was established in 1900. As a requirement, all articles must be more than 15 printed pages. Its ISSN number is 0002-9947. See also * ''Bulletin of the American Mathematical Society'' * ''Journal of the American Mathematical Society'' * '' Memoirs of the American Mathematical Society'' * '' Notices of the American Mathematical Society'' * ''Proceedings of the American Mathematical Society'' References External links * ''Transactions of the American Mathematical Society''on JSTOR JSTOR ( ; short for ''Journal Storage'') is a digital library of academic journals, books, and primary sources founded in 1994. Originally containing digitized back issues of academic journals, it now encompasses books and other primary source ... American Mathematical Society academic journals Mathematics jo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Publications Math├®matiques De L'IH├ēS
''Publications Math├®matiques de l'IH├ēS'' is a peer-reviewed mathematical journal. It is published by Springer Science+Business Media on behalf of the Institut des Hautes ├ētudes Scientifiques, with the help of the Centre National de la Recherche Scientifique. The journal was established in 1959 and was published at irregular intervals, from one to five volumes a year. It is now biannual. The editor-in-chief is S├®bastien Boucksom (CNRS, Institut de Math├®matique de Jussieu). See also *''Annals of Mathematics The ''Annals of Mathematics'' is a mathematical journal published every two months by Princeton University and the Institute for Advanced Study. History The journal was established as ''The Analyst'' in 1874 and with Joel E. Hendricks as t ...'' *'' Journal of the American Mathematical Society'' *'' Inventiones Mathematicae'' External links * Back issues from 1959 to 2010 Mathematics journals Academic journals established in 1959 Springer Science+Business Me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
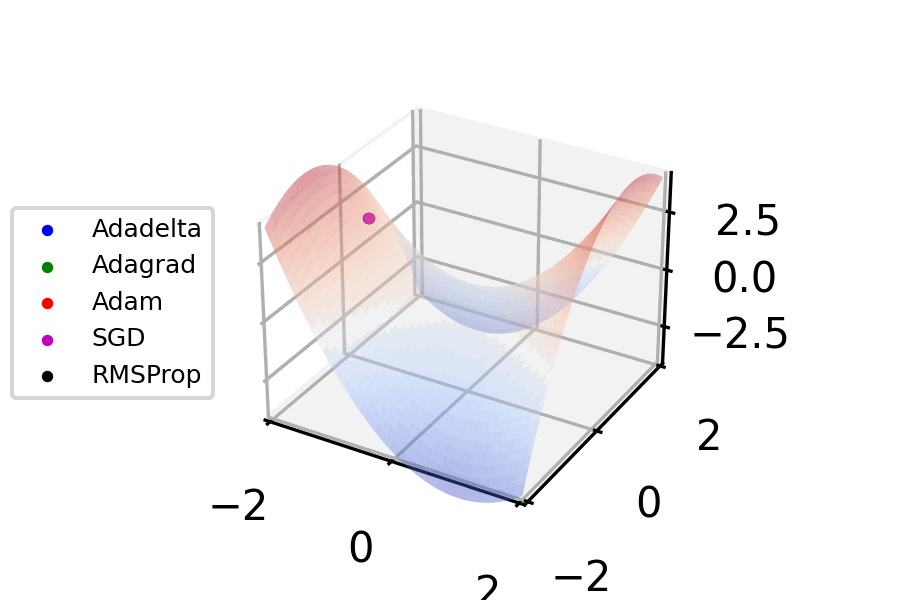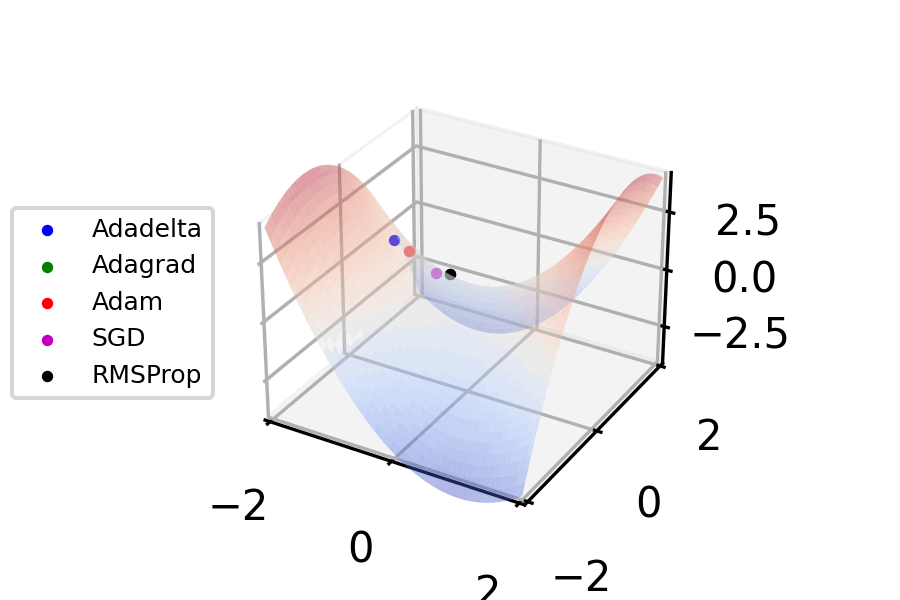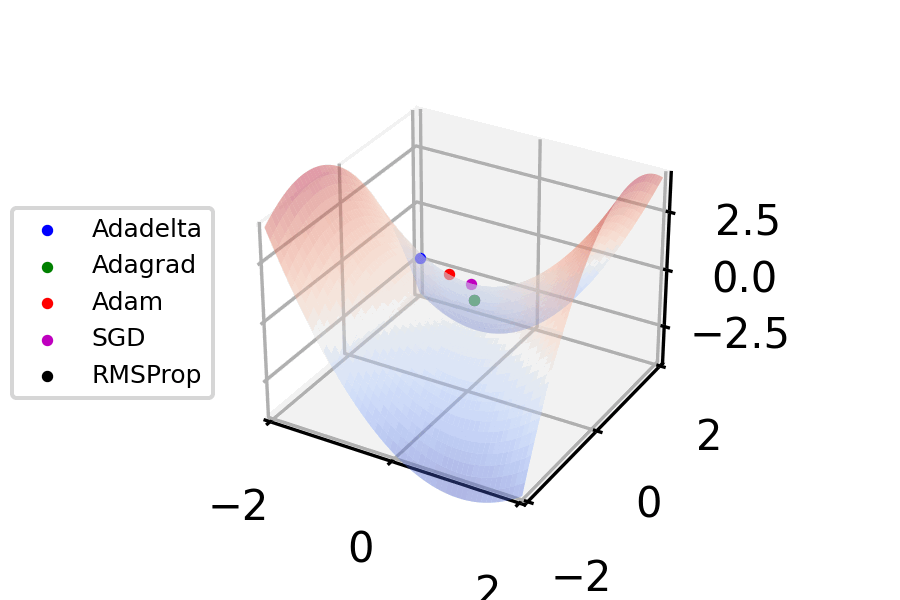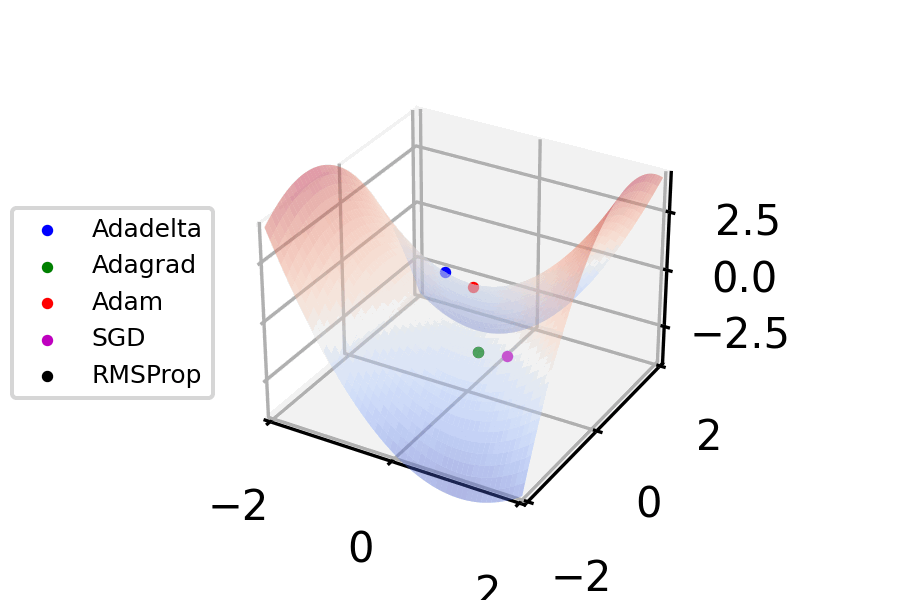
Stochastic Gradient Descent
Stochastic gradient descent (often abbreviated SGD) is an Iterative method, iterative method for optimizing an objective function with suitable smoothness properties (e.g. Differentiable function, differentiable or Subderivative, subdifferentiable). It can be regarded as a stochastic approximation of gradient descent optimization, since it replaces the actual gradient (calculated from the entire data set) by an estimate thereof (calculated from a randomly selected subset of the data). Especially in high-dimensional optimization problems this reduces the very high Computational complexity, computational burden, achieving faster iterations in exchange for a lower Rate of convergence, convergence rate. The basic idea behind stochastic approximation can be traced back to the RobbinsŌĆōMonro algorithm of the 1950s. Today, stochastic gradient descent has become an important optimization method in machine learning. Background Both statistics, statistical M-estimation, estimation and ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coordinate Descent
Coordinate descent is an optimization algorithm that successively minimizes along coordinate directions to find the minimum of a function. At each iteration, the algorithm determines a coordinate or coordinate block via a coordinate selection rule, then exactly or inexactly minimizes over the corresponding coordinate hyperplane while fixing all other coordinates or coordinate blocks. A line search along the coordinate direction can be performed at the current iterate to determine the appropriate step size. Coordinate descent is applicable in both differentiable and derivative-free contexts. Description Coordinate descent is based on the idea that the minimization of a multivariable function F(\mathbf) can be achieved by minimizing it along one direction at a time, i.e., solving univariate (or at least much simpler) optimization problems in a loop. In the simplest case of ''cyclic coordinate descent'', one cyclically iterates through the directions, one at a time, minimizing the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line Search
In optimization, line search is a basic iterative approach to find a local minimum \mathbf^* of an objective function f:\mathbb R^n\to\mathbb R. It first finds a descent direction along which the objective function f will be reduced, and then computes a step size that determines how far \mathbf should move along that direction. The descent direction can be computed by various methods, such as gradient descent or quasi-Newton method. The step size can be determined either exactly or inexactly. One-dimensional line search Suppose ''f'' is a one-dimensional function, f:\mathbb R\to\mathbb R, and assume that it is unimodal, that is, contains exactly one local minimum ''x''* in a given interval 'a'',''z'' This means that ''f'' is strictly decreasing in ,x*and strictly increasing in *,''z'' There are several ways to find an (approximate) minimum point in this case. Zero-order methods Zero-order methods use only function evaluations (i.e., a value oracle) - not derivatives: * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Singular Value
In mathematics, in particular functional analysis, the singular values of a compact operator T: X \rightarrow Y acting between Hilbert spaces X and Y, are the square roots of the (necessarily non-negative) eigenvalues of the self-adjoint operator T^*T (where T^* denotes the adjoint of T). The singular values are non-negative real numbers, usually listed in decreasing order (''Žā''1(''T''), ''Žā''2(''T''), ŌĆ”). The largest singular value ''Žā''1(''T'') is equal to the operator norm of ''T'' (see Min-max theorem). If ''T'' acts on Euclidean space \Reals ^n, there is a simple geometric interpretation for the singular values: Consider the image by T of the unit sphere; this is an ellipsoid, and the lengths of its semi-axes are the singular values of T (the figure provides an example in \Reals^2). The singular values are the absolute values of the eigenvalues of a normal matrix ''A'', because the spectral theorem can be applied to obtain unitary diagonalization of A as A = U\Lambd ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strong Convexity
In mathematics, a real-valued function is called convex if the line segment between any two distinct points on the graph of the function lies above or on the graph between the two points. Equivalently, a function is convex if its ''epigraph'' (the set of points on or above the graph of the function) is a convex set. In simple terms, a convex function graph is shaped like a cup \cup (or a straight line like a linear function), while a concave function's graph is shaped like a cap \cap. A twice-differentiable function of a single variable is convex if and only if its second derivative is nonnegative on its entire domain. Well-known examples of convex functions of a single variable include a linear function f(x) = cx (where c is a real number), a quadratic function cx^2 (c as a nonnegative real number) and an exponential function ce^x (c as a nonnegative real number). Convex functions play an important role in many areas of mathematics. They are especially important in the s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |