Tetrahedral symmetry

150px, A regular tetrahedron, an example of a solid with full tetrahedral symmetry
A regular tetrahedron has 12 rotational (or orientation-preserving) symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.

The group of all (not necessarily orientation preserving) symmetries is isomorphic to the group S₄, the symmetric group of permutations of four objects, since there is exactly one such symmetry for each permutation of the vertices of the tetrahedron. The set of orientation-preserving symmetries forms a group referred to as the alternating subgroup A₄ of S₄.

Details

Chiral and full (or achiral tetrahedral symmetry and pyritohedral symmetry) are discrete point symmetries (or equivalently, symmetries on the sphere). They are among the crystallographic point groups of the cubic crystal system.

Seen in stereographic projection the edges of the tetrakis hexahedron form 6 circles (or centrally radial lines) in the plane. Each of these 6 circles represent a mirror line in tetrahedral symmetry. The intersection of these circles meet at order 2 and 3 gyration points.

Chiral tetrahedral symmetry

''T'', 332, ,3sup>+, or 23, of order 12 – chiral or rotational tetrahedral symmetry. There are three orthogonal 2-fold rotation axes, like chiral dihedral symmetry ''D''₂ or 222, with in addition four 3-fold axes, centered ''between'' the three orthogonal directions. This group is isomorphic to ''A''₄, the alternating group on 4 elements; in fact it is the group of even permutations of the four 3-fold axes: e, (123), (132), (124), (142), (134), (143), (234), (243), (12)(34), (13)(24), (14)(23).

The conjugacy classes of T are:
*identity
*4 × rotation by 120° clockwise (seen from a vertex): (234), (143), (412), (321)
*4 × rotation by 120° counterclockwise (ditto)
*3 × rotation by 180°

The rotations by 180°, together with the identity, form a normal subgroup of type Dih₂, with quotient group of type Z₃. The three elements of the latter are the identity, "clockwise rotation", and "anti-clockwise rotation", corresponding to permutations of the three orthogonal 2-fold axes, preserving orientation.

A₄ is the smallest group demonstrating that the converse of Lagrange's theorem is not true in general: given a finite group ''G'' and a divisor ''d'' of , ''G'', , there does not necessarily exist a subgroup of ''G'' with order ''d'': the group has no subgroup of order 6. Although it is a property for the abstract group in general, it is clear from the isometry group of chiral tetrahedral symmetry: because of the chirality the subgroup would have to be C₆ or D₃, but neither applies.

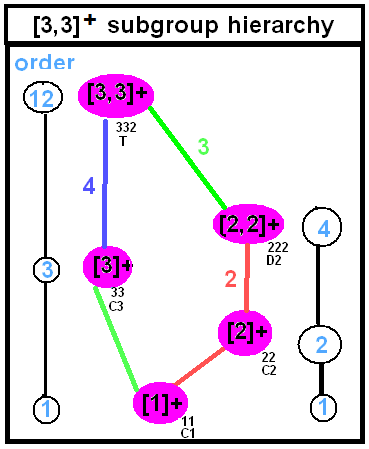
Subgroups of chiral tetrahedral symmetry

Achiral tetrahedral symmetry

T_d, *332, ,3or 3m, of order 24 – achiral or full tetrahedral symmetry, also known as the (2,3,3) triangle group. This group has the same rotation axes as T, but with six mirror planes, each through two 3-fold axes. The 2-fold axes are now S₄ () axes. T_d and O are isomorphic as abstract groups: they both correspond to S₄, the symmetric group on 4 objects. T_d is the union of T and the set obtained by combining each element of with inversion. See also the isometries of the regular tetrahedron.

The conjugacy classes of T_d are:
*identity
*8 × rotation by 120° (C₃)
*3 × rotation by 180° (C₂)
*6 × reflection in a plane through two rotation axes (C_s)
*6 × rotoreflection by 90° (S₄)

Subgroups of achiral tetrahedral symmetry

Pyritohedral symmetry

T_h, 3*2, ,3⁺or m, of order 24 – pyritohedral symmetry. This group has the same rotation axes as T, with mirror planes through two of the orthogonal directions. The 3-fold axes are now S₆ () axes, and there is a central inversion symmetry. T_h is isomorphic to : every element of T_h is either an element of T, or one combined with inversion. Apart from these two normal subgroups, there is also a normal subgroup D_2h (that of a cuboid), of type . It is the direct product of the normal subgroup of T (see above) with C_''i''. The quotient group is the same as above: of type Z₃. The three elements of the latter are the identity, "clockwise rotation", and "anti-clockwise rotation", corresponding to permutations of the three orthogonal 2-fold axes, preserving orientation.

It is the symmetry of a cube with on each face a line segment dividing the face into two equal rectangles, such that the line segments of adjacent faces do not meet at the edge. The symmetries correspond to the even permutations of the body diagonals and the same combined with inversion. It is also the symmetry of a pyritohedron, which is extremely similar to the cube described, with each rectangle replaced by a pentagon with one symmetry axis and 4 equal sides and 1 different side (the one corresponding to the line segment dividing the cube's face); i.e., the cube's faces bulge out at the dividing line and become narrower there. It is a subgroup of the full icosahedral symmetry group (as isometry group, not just as abstract group), with 4 of the 10 3-fold axes.

The conjugacy classes of T_h include those of T, with the two classes of 4 combined, and each with inversion:
*identity
*8 × rotation by 120° (C₃)
*3 × rotation by 180° (C₂)
*inversion (S₂)
*8 × rotoreflection by 60° (S₆)
*3 × reflection in a plane (C_s)

Subgroups of pyritohedral symmetry

Solids with chiral tetrahedral symmetry

The Icosahedron colored as a snub tetrahedron has chiral symmetry.

Solids with full tetrahedral symmetry

See also

* Octahedral symmetry
* Icosahedral symmetry
* Binary tetrahedral group
*

References

* Peter R. Cromwell, ''Polyhedra'' (1997), p. 295
* ''The Symmetries of Things'' 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass,
* ''Kaleidoscopes: Selected Writings of H.S.M. Coxeter'', edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995,

* Norman Johnson (mathematician), N.W. Johnson: ''Geometries and Transformations'', (2018) Chapter 11: ''Finite symmetry groups'', 11.5 Spherical Coxeter groups

External links

*

{{DEFAULTSORT:Tetrahedral Symmetry
Finite groups
Rotational symmetry