Shannon–Hartley theorem on:
[Wikipedia]
[Google]
[Amazon]
In information theory, the Shannon–Hartley theorem tells the maximum rate at which information can be transmitted over a communications channel of a specified
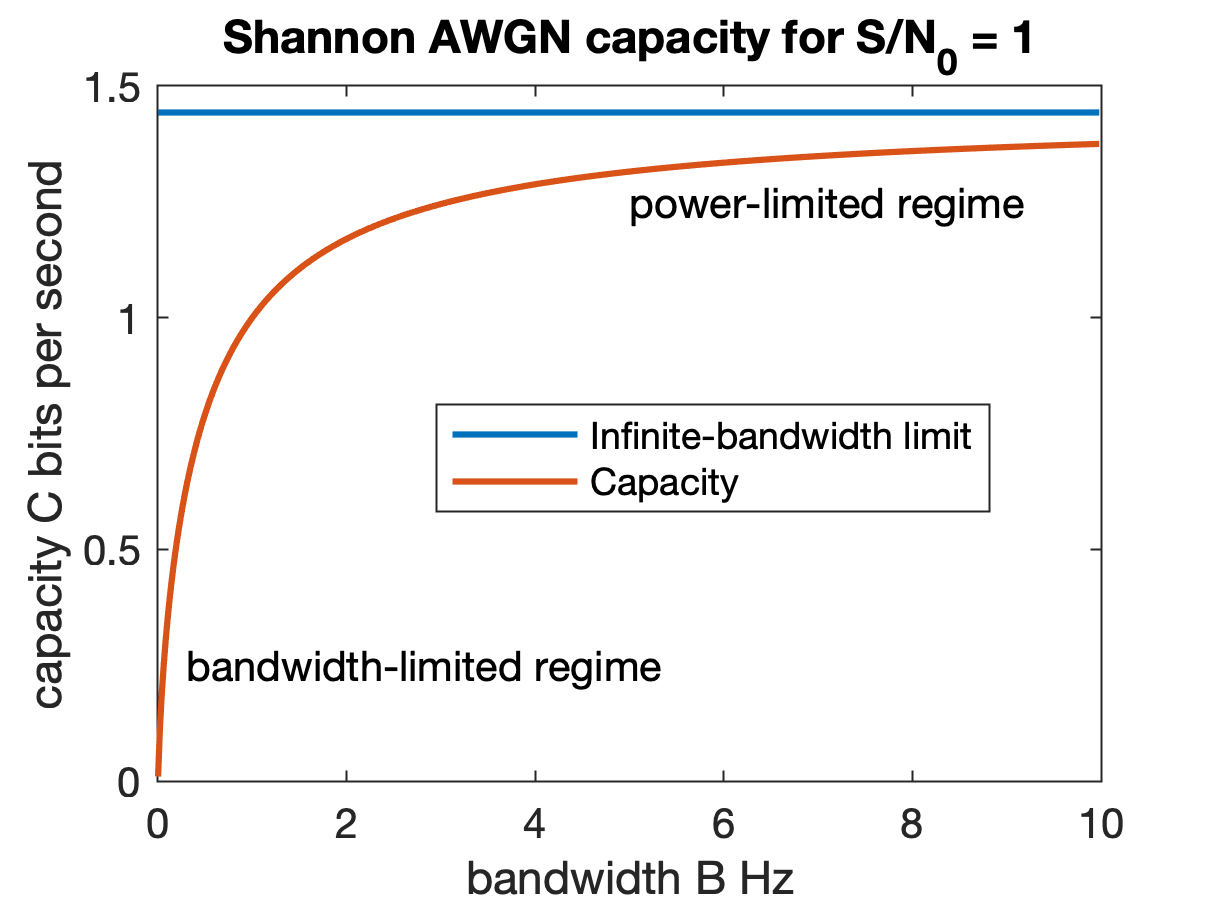 For large or small and constant signal-to-noise ratios, the capacity formula can be approximated:
For large or small and constant signal-to-noise ratios, the capacity formula can be approximated:
On-line textbook: Information Theory, Inference, and Learning Algorithms
by David MacKay - gives an entertaining and thorough introduction to Shannon theory, including two proofs of the noisy-channel coding theorem. This text also discusses state-of-the-art methods from coding theory, such as low-density parity-check codes, and
MIT News article on Shannon Limit
{{DEFAULTSORT:Shannon-Hartley theorem Information theory Telecommunication theory Mathematical theorems in theoretical computer science Theorems in statistics Claude Shannon
bandwidth
Bandwidth commonly refers to:
* Bandwidth (signal processing) or ''analog bandwidth'', ''frequency bandwidth'', or ''radio bandwidth'', a measure of the width of a frequency range
* Bandwidth (computing), the rate of data transfer, bit rate or thr ...
in the presence of noise
Noise is unwanted sound considered unpleasant, loud or disruptive to hearing. From a physics standpoint, there is no distinction between noise and desired sound, as both are vibrations through a medium, such as air or water. The difference aris ...
. It is an application of the noisy-channel coding theorem
In information theory, the noisy-channel coding theorem (sometimes Shannon's theorem or Shannon's limit), establishes that for any given degree of noise contamination of a communication channel, it is possible to communicate discrete data (di ...
to the archetypal case of a continuous-time analog
Analog or analogue may refer to:
Computing and electronics
* Analog signal, in which information is encoded in a continuous variable
** Analog device, an apparatus that operates on analog signals
*** Analog electronics, circuits which use analog ...
communications channel
A communication channel refers either to a physical transmission medium such as a wire, or to a logical connection over a multiplexed medium such as a radio channel in telecommunications and computer networking. A channel is used for informat ...
subject to Gaussian noise
Gaussian noise, named after Carl Friedrich Gauss, is a term from signal processing theory denoting a kind of signal noise that has a probability density function (pdf) equal to that of the normal distribution (which is also known as the Gaussian ...
. The theorem establishes Shannon's channel capacity for such a communication link, a bound on the maximum amount of error-free information
Information is an abstract concept that refers to that which has the power to inform. At the most fundamental level information pertains to the interpretation of that which may be sensed. Any natural process that is not completely random ...
per time unit that can be transmitted with a specified bandwidth
Bandwidth commonly refers to:
* Bandwidth (signal processing) or ''analog bandwidth'', ''frequency bandwidth'', or ''radio bandwidth'', a measure of the width of a frequency range
* Bandwidth (computing), the rate of data transfer, bit rate or thr ...
in the presence of the noise interference, assuming that the signal power is bounded, and that the Gaussian noise process is characterized by a known power or power spectral density. The law is named after Claude Shannon
Claude Elwood Shannon (April 30, 1916 – February 24, 2001) was an American mathematician, electrical engineer, and cryptographer known as a "father of information theory".
As a 21-year-old master's degree student at the Massachusetts Inst ...
and Ralph Hartley
Ralph Vinton Lyon Hartley (November 30, 1888 – May 1, 1970) was an American electronics researcher. He invented the Hartley oscillator and the Hartley transform, and contributed to the foundations of information theory.
Biography
Hartley wa ...
.
Statement of the theorem
The Shannon–Hartley theorem states the channel capacity , meaning the theoretical tightest upper bound on theinformation rate
In telecommunications and computing, bit rate (bitrate or as a variable ''R'') is the number of bits that are conveyed or processed per unit of time.
The bit rate is expressed in the unit bit per second (symbol: bit/s), often in conjunction w ...
of data that can be communicated at an arbitrarily low error rate using an average received signal power through an analog communication channel subject to additive white Gaussian noise (AWGN) of power
where
* is the channel capacity in bits per second, a theoretical upper bound on the net bit rate (information rate, sometimes denoted ) excluding error-correction codes;
* is the bandwidth
Bandwidth commonly refers to:
* Bandwidth (signal processing) or ''analog bandwidth'', ''frequency bandwidth'', or ''radio bandwidth'', a measure of the width of a frequency range
* Bandwidth (computing), the rate of data transfer, bit rate or thr ...
of the channel in hertz
The hertz (symbol: Hz) is the unit of frequency in the International System of Units (SI), equivalent to one event (or cycle) per second. The hertz is an SI derived unit whose expression in terms of SI base units is s−1, meaning that o ...
(passband
A passband is the range of frequencies or wavelengths that can pass through a filter. For example, a radio receiver contains a bandpass filter to select the frequency of the desired radio signal out of all the radio waves picked up by its antenn ...
bandwidth in case of a bandpass signal);
* is the average received signal power over the bandwidth (in case of a carrier-modulated passband transmission, often denoted '' C''), measured in watts (or volts squared);
* is the average power of the noise and interference over the bandwidth, measured in watts (or volts squared); and
* is the signal-to-noise ratio (SNR) or the carrier-to-noise ratio (CNR) of the communication signal to the noise and interference at the receiver (expressed as a linear power ratio, not as logarithmic decibels).
Historical development
During the late 1920s,Harry Nyquist
Harry Nyquist (, ; February 7, 1889 – April 4, 1976) was a Swedish-American physicist and electronic engineer who made important contributions to communication theory.
Personal life
Nyquist was born in the village Nilsby of the parish Stora Ki ...
and Ralph Hartley
Ralph Vinton Lyon Hartley (November 30, 1888 – May 1, 1970) was an American electronics researcher. He invented the Hartley oscillator and the Hartley transform, and contributed to the foundations of information theory.
Biography
Hartley wa ...
developed a handful of fundamental ideas related to the transmission of information, particularly in the context of the telegraph
Telegraphy is the long-distance transmission of messages where the sender uses symbolic codes, known to the recipient, rather than a physical exchange of an object bearing the message. Thus flag semaphore is a method of telegraphy, whereas p ...
as a communications system. At the time, these concepts were powerful breakthroughs individually, but they were not part of a comprehensive theory. In the 1940s, Claude Shannon
Claude Elwood Shannon (April 30, 1916 – February 24, 2001) was an American mathematician, electrical engineer, and cryptographer known as a "father of information theory".
As a 21-year-old master's degree student at the Massachusetts Inst ...
developed the concept of channel capacity, based in part on the ideas of Nyquist and Hartley, and then formulated a complete theory of information and its transmission.
Nyquist rate
In 1927, Nyquist determined that the number of independent pulses that could be put through a telegraph channel per unit time is limited to twice thebandwidth
Bandwidth commonly refers to:
* Bandwidth (signal processing) or ''analog bandwidth'', ''frequency bandwidth'', or ''radio bandwidth'', a measure of the width of a frequency range
* Bandwidth (computing), the rate of data transfer, bit rate or thr ...
of the channel. In symbolic notation,
:
where is the pulse frequency (in pulses per second) and is the bandwidth (in hertz). The quantity later came to be called the ''Nyquist rate
In signal processing, the Nyquist rate, named after Harry Nyquist, is a value (in units of samples per second or hertz, Hz) equal to twice the highest frequency ( bandwidth) of a given function or signal. When the function is digitized at a hi ...
'', and transmitting at the limiting pulse rate of pulses per second as ''signalling at the Nyquist rate''. Nyquist published his results in 1928 as part of his paper "Certain topics in Telegraph Transmission Theory".
Also 2002 Reprint
Hartley's law
During 1928, Hartley formulated a way to quantify information and itsline rate
In telecommunications and computing, bit rate (bitrate or as a variable ''R'') is the number of bits that are conveyed or processed per unit of time.
The bit rate is expressed in the unit bit per second (symbol: bit/s), often in conjunction w ...
(also known as data signalling rate ''R'' bits per second). This method, later known as Hartley's law, became an important precursor for Shannon's more sophisticated notion of channel capacity.
Hartley argued that the maximum number of distinguishable pulse levels that can be transmitted and received reliably over a communications channel is limited by the dynamic range of the signal amplitude and the precision with which the receiver can distinguish amplitude levels. Specifically, if the amplitude of the transmitted signal is restricted to the range of ��''A'' ... +''A''volts, and the precision of the receiver is ±Δ''V'' volts, then the maximum number of distinct pulses ''M'' is given by
:.
By taking information per pulse in bit/pulse to be the base-2-logarithm
In mathematics, the logarithm is the inverse function to exponentiation. That means the logarithm of a number to the base is the exponent to which must be raised, to produce . For example, since , the ''logarithm base'' 10 of ...
of the number of distinct messages ''M'' that could be sent, Hartley constructed a measure of the line rate ''R'' as:
:
where is the pulse rate, also known as the symbol rate, in symbols/second or baud.
Hartley then combined the above quantification with Nyquist's observation that the number of independent pulses that could be put through a channel of bandwidth hertz
The hertz (symbol: Hz) is the unit of frequency in the International System of Units (SI), equivalent to one event (or cycle) per second. The hertz is an SI derived unit whose expression in terms of SI base units is s−1, meaning that o ...
was pulses per second, to arrive at his quantitative measure for achievable line rate.
Hartley's law is sometimes quoted as just a proportionality between the analog bandwidth, , in Hertz and what today is called the digital bandwidth, , in bit/s.
Other times it is quoted in this more quantitative form, as an achievable line rate of bits per second:
:
Hartley did not work out exactly how the number ''M'' should depend on the noise statistics of the channel, or how the communication could be made reliable even when individual symbol pulses could not be reliably distinguished to ''M'' levels; with Gaussian noise statistics, system designers had to choose a very conservative value of to achieve a low error rate.
The concept of an error-free capacity awaited Claude Shannon, who built on Hartley's observations about a logarithmic measure of information and Nyquist's observations about the effect of bandwidth limitations.
Hartley's rate result can be viewed as the capacity of an errorless ''M''-ary channel of symbols per second. Some authors refer to it as a capacity. But such an errorless channel is an idealization, and if M is chosen small enough to make the noisy channel nearly errorless, the result is necessarily less than the Shannon capacity of the noisy channel of bandwidth , which is the Hartley–Shannon result that followed later.
Noisy channel coding theorem and capacity
Claude Shannon
Claude Elwood Shannon (April 30, 1916 – February 24, 2001) was an American mathematician, electrical engineer, and cryptographer known as a "father of information theory".
As a 21-year-old master's degree student at the Massachusetts Inst ...
's development of information theory during World War II provided the next big step in understanding how much information could be reliably communicated through noisy channels. Building on Hartley's foundation, Shannon's noisy channel coding theorem (1948) describes the maximum possible efficiency of error-correcting methods versus levels of noise interference and data corruption. The proof of the theorem shows that a randomly constructed error-correcting code is essentially as good as the best possible code; the theorem is proved through the statistics of such random codes.
Shannon's theorem shows how to compute a channel capacity from a statistical description of a channel, and establishes that given a noisy channel with capacity and information transmitted at a line rate , then if
:
there exists a coding technique which allows the probability of error at the receiver to be made arbitrarily small. This means that theoretically, it is possible to transmit information nearly without error up to nearly a limit of bits per second.
The converse is also important. If
:
the probability of error at the receiver increases without bound as the rate is increased. So no useful information can be transmitted beyond the channel capacity. The theorem does not address the rare situation in which rate and capacity are equal.
The Shannon–Hartley theorem establishes what that channel capacity is for a finite-bandwidth continuous-time channel subject to Gaussian noise. It connects Hartley's result with Shannon's channel capacity theorem in a form that is equivalent to specifying the ''M'' in Hartley's line rate formula in terms of a signal-to-noise ratio, but achieving reliability through error-correction coding rather than through reliably distinguishable pulse levels.
If there were such a thing as a noise-free analog channel, one could transmit unlimited amounts of error-free data over it per unit of time (Note that an infinite-bandwidth analog channel couldn’t transmit unlimited amounts of error-free data absent infinite signal power). Real channels, however, are subject to limitations imposed by both finite bandwidth and nonzero noise.
Bandwidth and noise affect the rate at which information can be transmitted over an analog channel. Bandwidth limitations alone do not impose a cap on the maximum information rate because it is still possible for the signal to take on an indefinitely large number of different voltage levels on each symbol pulse, with each slightly different level being assigned a different meaning or bit sequence. Taking into account both noise and bandwidth limitations, however, there is a limit to the amount of information that can be transferred by a signal of a bounded power, even when sophisticated multi-level encoding techniques are used.
In the channel considered by the Shannon–Hartley theorem, noise and signal are combined by addition. That is, the receiver measures a signal that is equal to the sum of the signal encoding the desired information and a continuous random variable that represents the noise. This addition creates uncertainty as to the original signal's value. If the receiver has some information about the random process that generates the noise, one can in principle recover the information in the original signal by considering all possible states of the noise process. In the case of the Shannon–Hartley theorem, the noise is assumed to be generated by a Gaussian process with a known variance. Since the variance of a Gaussian process is equivalent to its power, it is conventional to call this variance the noise power.
Such a channel is called the Additive White Gaussian Noise channel, because Gaussian noise is added to the signal; "white" means equal amounts of noise at all frequencies within the channel bandwidth. Such noise can arise both from random sources of energy and also from coding and measurement error at the sender and receiver respectively. Since sums of independent Gaussian random variables are themselves Gaussian random variables, this conveniently simplifies analysis, if one assumes that such error sources are also Gaussian and independent.
Implications of the theorem
Comparison of Shannon's capacity to Hartley's law
Comparing the channel capacity to the information rate from Hartley's law, we can find the effective number of distinguishable levels ''M'': : : The square root effectively converts the power ratio back to a voltage ratio, so the number of levels is approximately proportional to the ratio of signal RMS amplitude to noise standard deviation. This similarity in form between Shannon's capacity and Hartley's law should not be interpreted to mean that pulse levels can be literally sent without any confusion. More levels are needed to allow for redundant coding and error correction, but the net data rate that can be approached with coding is equivalent to using that in Hartley's law.Frequency-dependent (colored noise) case
In the simple version above, the signal and noise are fully uncorrelated, in which case is the total power of the received signal and noise together. A generalization of the above equation for the case where the additive noise is not white (or that the is not constant with frequency over the bandwidth) is obtained by treating the channel as many narrow, independent Gaussian channels in parallel: : where * is the channel capacity in bits per second; * is the bandwidth of the channel in Hz; * is the signalpower spectrum
The power spectrum S_(f) of a time series x(t) describes the distribution of power into frequency components composing that signal. According to Fourier analysis, any physical signal can be decomposed into a number of discrete frequencies, ...
* is the noise power spectrum
* is frequency in Hz.
Note: the theorem only applies to Gaussian stationary process
In mathematics and statistics, a stationary process (or a strict/strictly stationary process or strong/strongly stationary process) is a stochastic process whose unconditional joint probability distribution does not change when shifted in time. Con ...
noise. This formula's way of introducing frequency-dependent noise cannot describe all continuous-time noise processes. For example, consider a noise process consisting of adding a random wave whose amplitude is 1 or −1 at any point in time, and a channel that adds such a wave to the source signal. Such a wave's frequency components are highly dependent. Though such a noise may have a high power, it is fairly easy to transmit a continuous signal with much less power than one would need if the underlying noise was a sum of independent noises in each frequency band.
Approximations
 For large or small and constant signal-to-noise ratios, the capacity formula can be approximated:
For large or small and constant signal-to-noise ratios, the capacity formula can be approximated:
Bandwidth-limited case
When the SNR is large (), the logarithm is approximated by : in which case the capacity is logarithmic in power and approximately linear in bandwidth (not quite linear, since increases with bandwidth, imparting a logarithmic effect). This is called the bandwidth-limited regime. : where :Power-limited case
Similarly, when the SNR is small (if ), applying the approximation to the logarithm: : then the capacity is linear in power. This is called the power-limited regime. : In this low-SNR approximation, capacity is independent of bandwidth if the noise is white, ofspectral density
The power spectrum S_(f) of a time series x(t) describes the distribution of power into frequency components composing that signal. According to Fourier analysis, any physical signal can be decomposed into a number of discrete frequencies, ...
watts per hertz, in which case the total noise power is .
:
Examples
# At a SNR of 0 dB (Signal power = Noise power) the Capacity in bits/s is equal to the bandwidth in hertz. # If the SNR is 20 dB, and the bandwidth available is 4 kHz, which is appropriate for telephone communications, then C = 4000 log2(1 + 100) = 4000 log2 (101) = 26.63 kbit/s. Note that the value of S/N = 100 is equivalent to the SNR of 20 dB. # If the requirement is to transmit at 50 kbit/s, and a bandwidth of 10 kHz is used, then the minimum S/N required is given by 50000 = 10000 log2(1+S/N) so C/B = 5 then S/N = 25 − 1 = 31, corresponding to an SNR of 14.91 dB (10 x log10(31)). # What is the channel capacity for a signal having a 1 MHz bandwidth, received with a SNR of −30 dB ? That means a signal deeply buried in noise. −30 dB means a S/N = 10−3. It leads to a maximal rate of information of 106 log2 (1 + 10−3) = 1443 bit/s. These values are typical of the received ranging signals of the GPS, where the navigation message is sent at 50 bit/s (below the channel capacity for the given S/N), and whose bandwidth is spread to around 1 MHz by a pseudo-noise multiplication before transmission. # As stated above, channel capacity is proportional to the bandwidth of the channel and to the logarithm of SNR. This means channel capacity can be increased linearly either by increasing the channel's bandwidth given a fixed SNR requirement or, with fixed bandwidth, by using higher-order modulations that need a very high SNR to operate. As the modulation rate increases, thespectral efficiency
Spectral efficiency, spectrum efficiency or bandwidth efficiency refers to the information rate that can be transmitted over a given Bandwidth (signal processing), bandwidth in a specific communication system. It is a measure of how efficiently a l ...
improves, but at the cost of the SNR requirement. Thus, there is an exponential rise in the SNR requirement if one adopts a 16QAM or 64QAM (see: Quadrature amplitude modulation
Quadrature amplitude modulation (QAM) is the name of a family of digital modulation methods and a related family of analog modulation methods widely used in modern telecommunications to transmit information. It conveys two analog message signa ...
); however, the spectral efficiency improves.
See also
*Nyquist–Shannon sampling theorem
The Nyquist–Shannon sampling theorem is a theorem in the field of signal processing which serves as a fundamental bridge between continuous-time signals and discrete-time signals. It establishes a sufficient condition for a sample rate that per ...
* Eb/N0
Notes
References
* *External links
On-line textbook: Information Theory, Inference, and Learning Algorithms
by David MacKay - gives an entertaining and thorough introduction to Shannon theory, including two proofs of the noisy-channel coding theorem. This text also discusses state-of-the-art methods from coding theory, such as low-density parity-check codes, and
Turbo code
In information theory, turbo codes (originally in French ''Turbocodes'') are a class of high-performance forward error correction (FEC) codes developed around 1990–91, but first published in 1993. They were the first practical codes to closel ...
s.
MIT News article on Shannon Limit
{{DEFAULTSORT:Shannon-Hartley theorem Information theory Telecommunication theory Mathematical theorems in theoretical computer science Theorems in statistics Claude Shannon