hyperbolic angle

In geometry, hyperbolic angle is a real number determined by the area of the corresponding hyperbolic sector of ''xy'' = 1 in Quadrant I of the Cartesian plane. The hyperbolic angle parametrises the unit hyperbola, which has hyperbolic functions as coordinates. In mathematics, hyperbolic angle is an invariant measure as it is preserved under hyperbolic rotation.

The hyperbola ''xy'' = 1 is rectangular with a semi-major axis of $\sqrt 2$, analogous to the magnitude of a circular angle corresponding to the area of a circular sector in a circle with radius $\sqrt 2$.

Hyperbolic angle is used as the independent variable for the hyperbolic functions sinh, cosh, and tanh, because these functions may be premised on hyperbolic analogies to the corresponding circular trigonometric functions by regarding a hyperbolic angle as defining a hyperbolic triangle.
The parameter thus becomes one of the most useful in the calculus of real variables.

Definition

Consider the rectangular hyperbola $\textstyle\$, and (by convention) pay particular attention to the ''branch'' $x > 1$.

First define:
* The hyperbolic angle in ''standard position'' is the angle at $(0, 0)$ between the ray to $(1, 1)$ and the ray to $\textstyle(x, \frac 1 x)$, where $x > 1$.
* The magnitude of this angle is the area of the corresponding hyperbolic sector, which turns out to be $\operatornamex$.

Note that, because of the role played by the natural logarithm:
* Unlike the circular angle, the hyperbolic angle is ''unbounded'' (because $\operatornamex$ is unbounded); this is related to the fact that the harmonic series is unbounded.
* The formula for the magnitude of the angle suggests that, for $0 < x < 1$, the hyperbolic angle should be negative. This reflects the fact that, as defined, the angle is ''directed''.

Finally, extend the definition of ''hyperbolic angle'' to that subtended by any interval on the hyperbola. Suppose $a, b, c, d$ are positive real numbers such that $ab = cd = 1$ and $c > a > 1$, so that $(a, b)$ and $(c, d)$ are points on the hyperbola $xy=1$ and determine an interval on it. Then the squeeze mapping $\textstyle f:(x, y)\to(bx, ay)$ maps the angle $\angle\!\left ((a, b), (0,0), (c, d)\right)$ to the ''standard position'' angle $\angle\!\left ((1, 1), (0,0), (bc, ad)\right)$. By the result of Gregoire de Saint-Vincent, the hyperbolic sectors determined by these angles have the same area, which is taken to be the magnitude of the angle. This magnitude is $\operatorname=\operatorname(c/a) =\operatornamec-\operatornamea$.

Comparison with circular angle

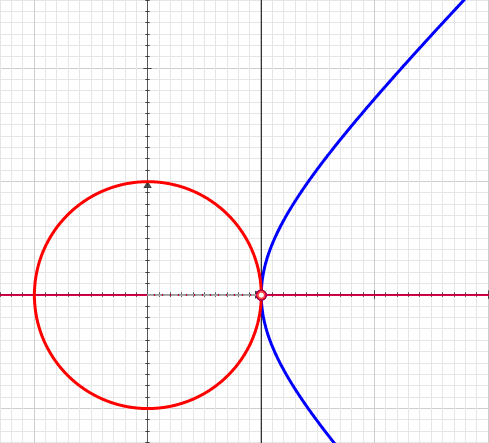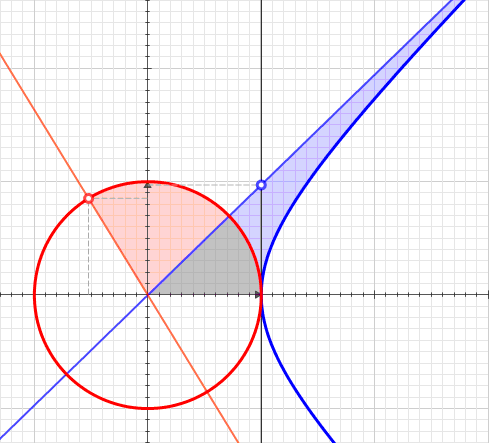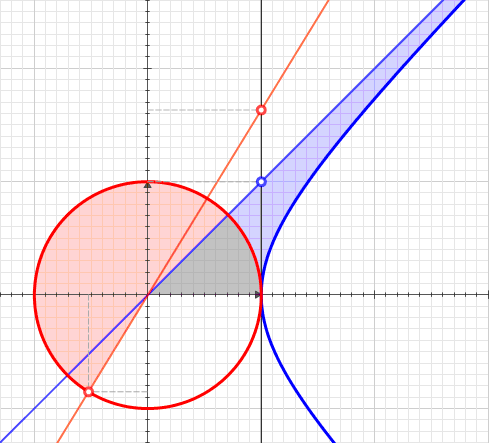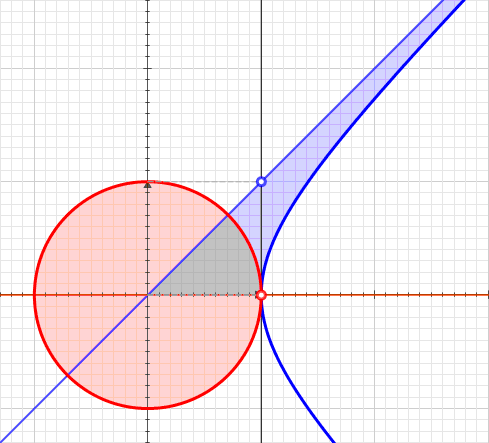
A unit circle $x^2 + y^2 = 1$ has a circular sector with an area half of the circular angle in radians. Analogously, a unit hyperbola $x^2 - y^2 = 1$ has a hyperbolic sector with an area half of the hyperbolic angle.

There is also a projective resolution between circular and hyperbolic cases: both curves are conic sections, and hence are treated as projective ranges in projective geometry. Given an origin point on one of these ranges, other points correspond to angles. The idea of addition of angles, basic to science, corresponds to addition of points on one of these ranges as follows:

Circular angles can be characterised geometrically by the property that if two chords ''P''₀''P''₁ and ''P''₀''P''₂ subtend angles ''L''₁ and ''L''₂ at the centre of a circle, their sum is the angle subtended by a chord ''PQ'', where ''PQ'' is required to be parallel to ''P''₁''P''₂.

The same construction can also be applied to the hyperbola. If ''P''₀ is taken to be the point , ''P''₁ the point , and ''P''₂ the point , then the parallel condition requires that ''Q'' be the point . It thus makes sense to define the hyperbolic angle from ''P''₀ to an arbitrary point on the curve as a logarithmic function of the point's value of ''x''.

Whereas in Euclidean geometry moving steadily in an orthogonal direction to a ray from the origin traces out a circle, in a pseudo-Euclidean plane steadily moving orthogonally to a ray from the origin traces out a hyperbola. In Euclidean space, the multiple of a given angle traces equal distances around a circle while it traces exponential distances upon the hyperbolic line.

Both circular and hyperbolic angle provide instances of an invariant measure. Arcs with an angular magnitude on a circle generate a measure on certain measurable sets on the circle whose magnitude does not vary as the circle turns or rotates. For the hyperbola the turning is by squeeze mapping, and the hyperbolic angle magnitudes stay the same when the plane is squeezed by a mapping
:(''x'', ''y'') ↦ (''rx'', ''y'' / ''r''), with ''r'' > 0 .

Relation To The Minkowski Line Element

There is also a curious relation to a hyperbolic angle and the metric defined on Minkowski space. Just as two dimensional Euclidean geometry defines its line element as
:$ds_^2 = dx^2 + dy^2,$
the line element on Minkowski space is
:$ds_^2 = dx^2 - dy^2.$

Consider a curve imbedded in two dimensional Euclidean space,
:$x = f(t), y=g(t).$
Where the parameter $t$ is a real number that runs between $a$ and $b$ ($a\leqslant t$). The arclength of this curve in Euclidean space is computed as:
:$S = \int_^ds_ = \int_^ \sqrtdt.$

If $x^2 + y^2 = 1$ defines a unit circle, a single parameterized solution set to this equation is $x = \cos t$ and $y = \sin t$. Letting $0\leqslant t < \theta$, computing the arclength $S$ gives $S = \theta$. Now doing the same procedure, except replacing the Euclidean element with the Minkowski line element,
:$S = \int_^ds_ = \int_^ \sqrtdt,$
and defined a "unit" hyperbola as $y^2 - x^2 = 1$ with its corresponding parameterized solution set $y = \cosh t$ and $x = \sinh t$, and by letting $0\leqslant t < \eta$ (the hyperbolic angle), we arrive at the result of $S = \eta$. In other words, this means just as how the circular angle can be defined as the arclength of an arc on the unit circle subtended by the same angle using the Euclidean defined metric, the hyperbolic angle is the arclength of the arc on the "unit" hyperbola subtended by the hyperbolic angle using the Minkowski defined metric.

History

The quadrature of the hyperbola is the evaluation of the area of a hyperbolic sector. It can be shown to be equal to the corresponding area against an asymptote. The quadrature was first accomplished by Gregoire de Saint-Vincent in 1647 in ''Opus geometricum quadrature circuli et sectionum coni''. As expressed by a historian,
: e made thequadrature of a hyperbola to its asymptotes, and showed that as the area increased in arithmetic series the abscissas increased in geometric series.

A. A. de Sarasa interpreted the quadrature as a logarithm and thus the geometrically defined natural logarithm (or "hyperbolic logarithm") is understood as the area under to the right of . As an example of a transcendental function, the logarithm is more familiar than its motivator, the hyperbolic angle. Nevertheless, the hyperbolic angle plays a role when the theorem of Saint-Vincent is advanced with squeeze mapping.

Circular trigonometry was extended to the hyperbola by Augustus De Morgan in his textbook ''Trigonometry and Double Algebra''. In 1878 W.K. Clifford used the hyperbolic angle to parametrize a unit hyperbola, describing it as "quasi- harmonic motion".

In 1894 Alexander Macfarlane circulated his essay "The Imaginary of Algebra", which used hyperbolic angles to generate hyperbolic versors, in his book ''Papers on Space Analysis''. The following year Bulletin of the American Mathematical Society published Mellen W. Haskell's outline of the hyperbolic functions.

When Ludwik Silberstein penned his popular 1914 textbook on the new theory of relativity, he used the rapidity concept based on hyperbolic angle ''a'', where , the ratio of velocity ''v'' to the speed of light. He wrote:

:It seems worth mentioning that to ''unit'' rapidity corresponds a huge velocity, amounting to 3/4 of the velocity of light; more accurately we have for .
: ..the rapidity , ..consequently will represent the velocity .76 ''c'' which is a little above the velocity of light in water.

Silberstein also uses Lobachevsky's concept of angle of parallelism Π(''a'') to obtain . Ludwik Silberstein (1914
The Theory of Relativity
pp. 180–1 via Internet Archive

Imaginary circular angle

The hyperbolic angle is often presented as if it were an imaginary number, $\cos ix = \cosh x$ and $\sin ix = i \sinh x,$ so that the hyperbolic functions cosh and sinh can be presented through the circular functions. But in the Euclidean plane we might alternately consider circular angle measures to be imaginary and hyperbolic angle measures to be real scalars, $\cosh ix = \cos x$ and $\sinh ix = i \sin x.$

These relationships can be understood in terms of the exponential function, which for a complex argument $z$ can be broken into even and odd parts $\cosh z = \tfrac12(e^z + e^)$ and $\sinh z = \tfrac12(e^z - e^),$ respectively. Then

$e^z = \cosh z + \sinh z = \cos(iz) - i \sin(iz),$

or if the argument is separated into real and imaginary parts $z = x + iy,$ the exponential can be split into the product of scaling $e^$ and rotation $e^,$

$e^ = e^e^ = (\cosh x + \sinh x)(\cos y + i \sin y).$

As infinite series,

$\begin e^z &= \,\,\sum_^\infty \frac && = 1 + z + \tfracz^2 + \tfrac16z^3 + \tfrac1z^4 + \dots \\ \cosh z &= \sum_ \frac && = 1 + \tfracz^2 + \tfrac1z^4 + \dots \\ \sinh z &= \,\sum_ \frac && = z + \tfracz^3 + \tfrac1z^5 + \dots \\ \cos z &= \sum_ \frac && = 1 - \tfracz^2 + \tfrac1z^4 - \dots \\ i \sin z &= \,\sum_ \frac && = i\left(z - \tfracz^3 + \tfrac1z^5 - \dots\right) \\ \end$

The infinite series for cosine is derived from cosh by turning it into an alternating series, and the series for sine comes from making sinh into an alternating series.

See also

*Transcendent angle

Notes

References

* Janet Heine Barnett (2004) "Enter, stage center: the early drama of the hyperbolic functions", available in (a) Mathematics Magazine 77(1):15–30 or (b) chapter 7 of ''Euler at 300'', RE Bradley, LA D'Antonio, CE Sandifer editors, Mathematical Association of America .
* Arthur Kennelly (1912
Application of hyperbolic functions to electrical engineering problems
* William Mueller, ''Exploring Precalculus'', § The Number e


* John Stillwell (1998) ''Numbers and Geometry'' exercise 9.5.3, p. 298, Springer-Verlag .

{{DEFAULTSORT:Hyperbolic Angle
Angle
Differential calculus
Integral calculus