|
Projective Range
In mathematics, a projective range is a set of points in projective geometry considered in a unified fashion. A projective range may be a projective line or a conic. A projective range is the dual of a pencil of lines on a given point. For instance, a correlation interchanges the points of a projective range with the lines of a pencil. A projectivity is said to act from one range to another, though the two ranges may coincide as sets. A projective range expresses projective invariance of the relation of projective harmonic conjugates. Indeed, three points on a projective line determine a fourth by this relation. Application of a projectivity to this quadruple results in four points likewise in the harmonic relation. Such a quadruple of points is termed a harmonic range. In 1940 Julian Coolidge described this structure and identified its originator: :Two fundamental one-dimensional forms such as point ranges, pencils of lines, or of planes are defined as projective, when their mem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Oxford University Press
Oxford University Press (OUP) is the publishing house of the University of Oxford. It is the largest university press in the world. Its first book was printed in Oxford in 1478, with the Press officially granted the legal right to print books by decree in 1586. It is the second-oldest university press after Cambridge University Press, which was founded in 1534. It is a department of the University of Oxford. It is governed by a group of 15 academics, the Delegates of the Press, appointed by the Vice Chancellor, vice-chancellor of the University of Oxford. The Delegates of the Press are led by the Secretary to the Delegates, who serves as OUP's chief executive and as its major representative on other university bodies. Oxford University Press has had a similar governance structure since the 17th century. The press is located on Walton Street, Oxford, Walton Street, Oxford, opposite Somerville College, Oxford, Somerville College, in the inner suburb of Jericho, Oxford, Jericho. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hyperbolic Angle
In geometry, hyperbolic angle is a real number determined by the area of the corresponding hyperbolic sector of ''xy'' = 1 in Quadrant I of the Cartesian plane. The hyperbolic angle parametrizes the unit hyperbola, which has hyperbolic functions as coordinates. In mathematics, hyperbolic angle is an invariant measure as it is preserved under hyperbolic rotation. The hyperbola ''xy'' = 1 is rectangular with semi-major axis \sqrt 2, analogous to the circular angle equaling the area of a circular sector in a circle with radius \sqrt 2. Hyperbolic angle is used as the independent variable for the hyperbolic functions sinh, cosh, and tanh, because these functions may be premised on hyperbolic analogies to the corresponding circular (trigonometric) functions by regarding a hyperbolic angle as defining a hyperbolic triangle. The parameter thus becomes one of the most useful in the calculus of real variables. Definition Consider the rectangular hyperbola \textstyle\, and (by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two Ray (geometry), rays, called the ''Side (plane geometry), sides'' of the angle, sharing a common endpoint, called the ''vertex (geometry), vertex'' of the angle. More generally angles are also formed wherever two lines, rays or line segments come together, such as at the corners of triangles and other polygons. An angle can be considered as the region of the plane bounded by the sides. Angles can also be formed by the intersection of two planes or by two intersecting curves, in which case the rays lying tangent to each curve at the point of intersection define the angle. The term ''angle'' is also used for the size, magnitude (mathematics), magnitude or Physical quantity, quantity of these types of geometric figures and in this context an a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hyperbola
In mathematics, a hyperbola is a type of smooth function, smooth plane curve, curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected component (topology), connected components or branches, that are mirror images of each other and resemble two infinite bow (weapon), bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane (mathematics), plane and a double cone (geometry), cone. (The other conic sections are the parabola and the ellipse. A circle is a special case of an ellipse.) If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola. Besides being a conic section, a hyperbola can arise as the locus (mathematics), locus of points whose difference of distances to two fixed focus (geometry), foci is constant, as a curve for each point of which the rays to two fix ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting two points on the circle and passing through the centre is called the diameter. A circle bounds a region of the plane called a Disk (mathematics), disc. The circle has been known since before the beginning of recorded history. Natural circles are common, such as the full moon or a slice of round fruit. The circle is the basis for the wheel, which, with related inventions such as gears, makes much of modern machinery possible. In mathematics, the study of the circle has helped inspire the development of geometry, astronomy and calculus. Terminology * Annulus (mathematics), Annulus: a ring-shaped object, the region bounded by two concentric circles. * Circular arc, Arc: any Connected ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
American Mathematical Society
The American Mathematical Society (AMS) is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, and serves the national and international community through its publications, meetings, advocacy and other programs. The society is one of the four parts of the Joint Policy Board for Mathematics and a member of the Conference Board of the Mathematical Sciences. History The AMS was founded in 1888 as the New York Mathematical Society, the brainchild of Thomas Fiske, who was impressed by the London Mathematical Society on a visit to England. John Howard Van Amringe became the first president while Fiske became secretary. The society soon decided to publish a journal, but ran into some resistance over concerns about competing with the '' American Journal of Mathematics''. The result was the ''Bulletin of the American Mathematical Society'', with Fiske as editor-in-chief. The de facto journal, as intended, was influentia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Karl Von Staudt
Karl Georg Christian von Staudt (24 January 1798 – 1 June 1867) was a German mathematician who used synthetic geometry to provide a foundation for arithmetic. Life and influence Karl was born in the Free Imperial City of Rothenburg, which is now called Rothenburg ob der Tauber in Germany. From 1814 he studied in Gymnasium in Ausbach. He attended the University of Göttingen from 1818 to 1822 where he studied with Gauss who was director of the observatory. Staudt provided an ephemeris for the orbits of Mars and the asteroid Pallas. When in 1821 Comet Nicollet-Pons was observed, he provided the elements of its orbit. These accomplishments in astronomy earned him his doctorate from University of Erlangen in 1822. Staudt's professional career began as a secondary school instructor in Würzburg until 1827 and then Nuremberg until 1835. He married Jeanette Dreschler in 1832. They had a son Eduard and daughter Mathilda, but Jeanette died in 1848. The book ''Geometrie der Lage'' (184 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Dover Publications
Dover Publications, also known as Dover Books, is an American book publisher founded in 1941 by Hayward and Blanche Cirker. It primarily reissues books that are out of print from their original publishers. These are often, but not always, books in the public domain. The original published editions may be scarce or historically significant. Dover republishes these books, making them available at a significantly reduced cost. Classic reprints Dover reprints classic works of literature, classical sheet music, and public-domain images from the 18th and 19th centuries. Dover also publishes an extensive collection of mathematical, scientific, and engineering texts. It often targets its reprints at a niche market, such as woodworking. Starting in 2015, the company branched out into graphic novel reprints, overseen by Dover acquisitions editor and former comics writer and editor Drew Ford. Most Dover reprints are photo facsimiles of the originals, retaining the original pagination ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Julian Coolidge
Julian Lowell Coolidge (September 28, 1873 – March 5, 1954) was an American mathematician, historian, a professor and chairman of the Harvard University Mathematics Department. Biography Born in Brookline, Massachusetts, he graduated from Harvard University and Balliol College, Oxford. Between 1897 and 1899, Julian Coolidge taught at the Groton School, where one of his students was Franklin D. Roosevelt. He left Groton to accept a teaching position at Harvard and in 1902 was given an assistant professorship, but took two years off to further his education with studies in Turin, Italy before receiving his doctorate from the University of Bonn. Julian Coolidge then returned to teach at Harvard where he remained for his entire academic career, interrupted only by a year at the Sorbonne in Paris as an exchange professor. During World War I, he served with the U.S. Army's Overseas Expeditionary Force in France, rising to the rank of major. In 1919, he was awarded a Knight of Fra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Projective Geometry
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting (''projective space'') and a selective set of basic geometric concepts. The basic intuitions are that projective space has more points than Euclidean space, for a given dimension, and that geometric transformations are permitted that transform the extra points (called "Point at infinity, points at infinity") to Euclidean points, and vice versa. Properties meaningful for projective geometry are respected by this new idea of transformation, which is more radical in its effects than can be expressed by a transformation matrix and translation (geometry), translations (the affine transformations). The first issue for geometers is what kind of geometry is adequate for a novel situation. Unlike in Euclidean geometry, the concept of an angle does not ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
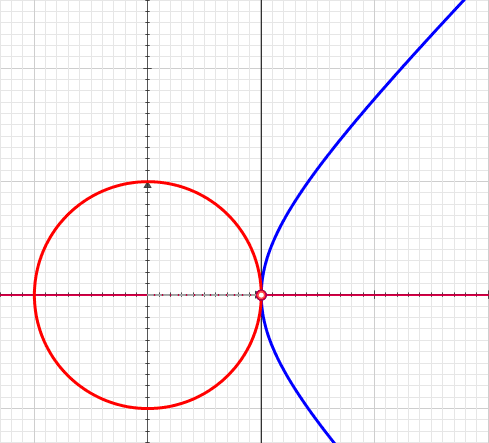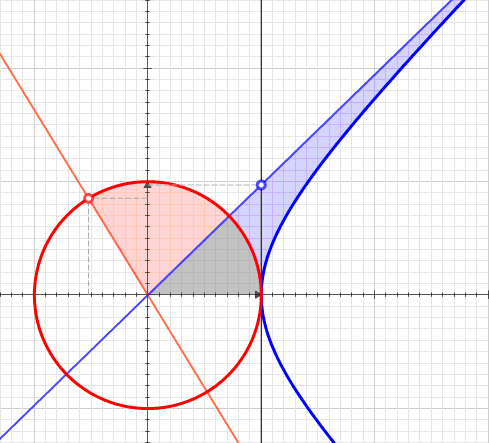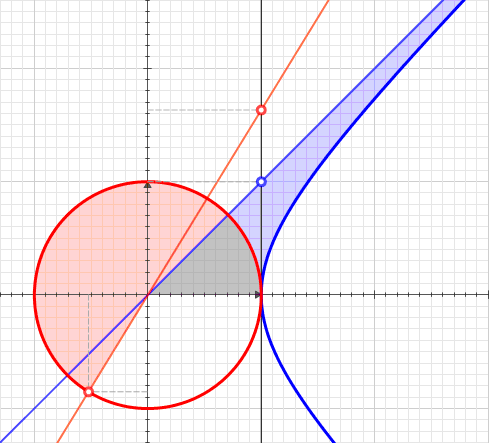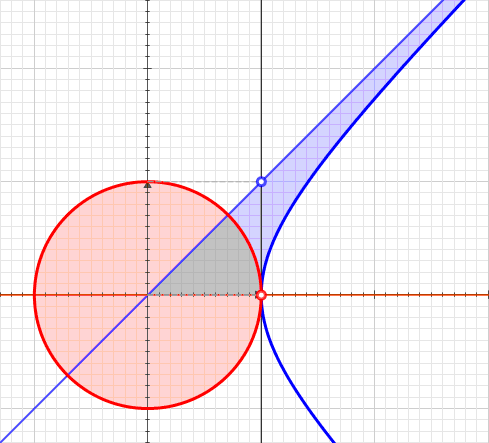
Projective Harmonic Conjugate
In projective geometry, the harmonic conjugate point of a point on the real projective line with respect to two other points is defined by the following construction: :Given three collinear points , let be a point not lying on their join and let any line through meet at respectively. If and meet at , and meets at , then is called the harmonic conjugate of with respect to and . The point does not depend on what point is taken initially, nor upon what line through is used to find and . This fact follows from Desargues theorem. In real projective geometry, harmonic conjugacy can also be defined in terms of the cross-ratio as . Cross-ratio criterion The four points are sometimes called a harmonic range (on the real projective line) as it is found that always divides the segment ''internally'' in the same proportion as divides ''externally''. That is: \overline:\overline = \overline:\overline \, . If these segments are now endowed with the ordinary metri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |