Homography

In projective geometry, a homography is an isomorphism of projective spaces, induced by an isomorphism of the vector spaces from which the projective spaces derive. It is a bijection that maps lines to lines, and thus a collineation. In general, some collineations are not homographies, but the fundamental theorem of projective geometry asserts that is not so in the case of real projective spaces of dimension at least two. Synonyms include projectivity, projective transformation, and projective collineation.

Historically, homographies (and projective spaces) have been introduced to study perspective and projections in Euclidean geometry, and the term ''homography'', which, etymologically, roughly means "similar drawing", dates from this time. At the end of the 19th century, formal definitions of projective spaces were introduced, which differed from extending Euclidean or affine spaces by adding points at infinity. The term "projective transformation" originated in these abstract constructions. These constructions divide into two classes that have been shown to be equivalent. A projective space may be constructed as the set of the lines of a vector space over a given field (the above definition is based on this version); this construction facilitates the definition of projective coordinates and allows using the tools of linear algebra for the study of homographies. The alternative approach consists in defining the projective space through a set of axioms, which do not involve explicitly any field (incidence geometry, see also synthetic geometry); in this context, collineations are easier to define than homographies, and homographies are defined as specific collineations, thus called "projective collineations".

For sake of simplicity, unless otherwise stated, the projective spaces considered in this article are supposed to be defined over a (commutative) field. Equivalently Pappus's hexagon theorem and Desargues's theorem are supposed to be true. A large part of the results remain true, or may be generalized to projective geometries for which these theorems do not hold.

Geometric motivation

Historically, the concept of homography had been introduced to understand, explain and study visual perspective, and, specifically, the difference in appearance of two plane objects viewed from different points of view.

In three-dimensional Euclidean space, a central projection from a point ''O'' (the center) onto a plane ''P'' that does not contain ''O'' is the mapping that sends a point ''A'' to the intersection (if it exists) of the line ''OA'' and the plane ''P''. The projection is not defined if the point ''A'' belongs to the plane passing through ''O'' and parallel to ''P''. The notion of projective space was originally introduced by extending the Euclidean space, that is, by adding points at infinity to it, in order to define the projection for every point except ''O''.

Given another plane ''Q'', which does not contain ''O'', the restriction to ''Q'' of the above projection is called a perspectivity.

With these definitions, a perspectivity is only a partial function, but it becomes a bijection if extended to projective spaces. Therefore, this notion is normally defined for projective spaces. The notion is also easily generalized to projective spaces of any dimension, over any field, in the following way:

If ''f'' is a perspectivity from ''P'' to ''Q'', and ''g'' a perspectivity from ''Q'' to ''P'', with a different center, then is a homography from ''P'' to itself, which is called a ''central collineation'', when the dimension of ''P'' is at least two. (See below and .)

Originally, a homography was defined as the composition of a finite number of perspectivities. It is a part of the fundamental theorem of projective geometry (see below) that this definition coincides with the more algebraic definition sketched in the introduction and detailed below.

Definition and expression in homogeneous coordinates

A projective space P(''V'') of dimension ''n'' over a field ''K'' may be defined as the set of the lines through the origin in a ''K''-vector space ''V'' of dimension . If a basis of ''V'' has been fixed, a point of ''V'' may be represented by a point $(x_0,\ldots,x_n)$ of ''K''^''n''+1. A point of P(''V''), being a line in ''V'', may thus be represented by the coordinates of any nonzero point of this line, which are thus called homogeneous coordinates of the projective point.

Given two projective spaces P(''V'') and P(''W'') of the same dimension, a homography is a mapping from P(''V'') to P(''W''), which is induced by an isomorphism of vector spaces $f:V\rightarrow W$. Such an isomorphism induces a bijection from P(''V'') to P(''W''), because of the linearity of ''f''. Two such isomorphisms, ''f'' and ''g'', define the same homography if and only if there is a nonzero element ''a'' of ''K'' such that .

This may be written in terms of homogeneous coordinates in the following way: A homography ''φ'' may be defined by a nonsingular matrix 'a''_''i'',''j'' called the ''matrix of the homography''. This matrix is defined up to the multiplication by a nonzero element of ''K''. The homogeneous coordinates _0:\cdots:x_n/math> of a point and the coordinates _0:\cdots:y_n/math> of its image by ''φ'' are related by
:$\begin y_0 &= a_x_0 +\dots + a_x_n\\ &\vdots\\ y_n &= a_x_0 +\dots + a_x_n. \end$

When the projective spaces are defined by adding points at infinity to affine spaces (projective completion) the preceding formulas become, in affine coordinates,
:$\begin y_1 &= \frac\\ &\vdots\\ y_n &= \frac \end$
which generalizes the expression of the homographic function of the next section. This defines only a partial function between affine spaces, which is defined only outside the hyperplane where the denominator is zero.

Homographies of a projective line

The projective line over a field ''K'' may be identified with the union of ''K'' and a point, called the "point at infinity" and denoted by ∞ (see projective line). With this representation of the projective line, the homographies are the mappings
:$z \mapsto \frac, \text ad - bc \neq 0,$
which are called homographic functions or linear fractional transformations.

In the case of the complex projective line, which can be identified with the Riemann sphere, the homographies are called Möbius transformations.
These correspond precisely with those bijections of the Riemann sphere that preserve orientation and are conformal.

In the study of collineations, the case of projective lines is special due to the small dimension. When the line is viewed as a projective space in isolation, any permutation of the points of a projective line is a collineation, since every set of points are collinear. However, if the projective line is embedded in a higher-dimensional projective space, the geometric structure of that space can be used to impose a geometric structure on the line. Thus, in synthetic geometry, the homographies and the collineations of the projective line that are considered are those obtained by restrictions to the line of collineations and homographies of spaces of higher dimension. This means that the fundamental theorem of projective geometry (see below) remains valid in the one-dimensional setting. A homography of a projective line may also be properly defined by insisting that the mapping preserves cross-ratios.

Projective frame and coordinates

A projective frame or projective basis of a projective space of dimension is an ordered set of points such that no hyperplane contains of them. A projective frame is sometimes called a simplex, although a simplex in a space of dimension has at most vertices.

Projective spaces over a commutative field are considered in this section, although most results may be generalized to projective spaces over a division ring.

Let be a projective space of dimension , where is a -vector space of dimension , and $p:V\setminus\\to P(V)$ be the canonical projection that maps a nonzero vector to the vector line that contains it.

For every frame of , there exists a basis $e_0, \dots, e_$ of such that the frame is $\left(p(e_0),\ldots, p(e_n),p(e_0+\dots+e_n)\right),$ and this basis is unique up to the multiplication of all its elements by the same nonzero element of . Conversely, if $e_0, \dots, e_$ is a basis of , then $\left(p(e_0), \ldots, p(e_n),p(e_0+\dots+e_n)\right)$ is a frame of

It follows that, given two frames, there is exactly one homography mapping the first one onto the second one. In particular, the only homography fixing the points of a frame is the identity map. This result is much more difficult in synthetic geometry (where projective spaces are defined through axioms). It is sometimes called the ''first fundamental theorem of projective geometry''.

Every frame $(p(e_0), \ldots, p(e_n), p(e_0+\cdots+e_n))$ allows to define ''projective coordinates'', also known as '' homogeneous coordinates'': every point may be written as ; the projective coordinates of on this frame are the coordinates of on the base $(e_0, \ldots, e_n).$ It is not difficult to verify that changing the $e_i$ and , without changing the frame nor ''p''(''v''), results in multiplying the projective coordinates by the same nonzero element of ''K''.

The projective space has a ''canonical frame'' consisting of the image by of the canonical basis of (consisting of the elements having only one nonzero entry, which is equal to 1), and . On this basis, the homogeneous coordinates of are simply the entries (coefficients) of the tuple . Given another projective space of the same dimension, and a frame of it, there is one and only one homography mapping onto the canonical frame of . The projective coordinates of a point on the frame are the homogeneous coordinates of on the canonical frame of .

Central collineations

In above sections, homographies have been defined through linear algebra. In synthetic geometry, they are traditionally defined as the composition of one or several special homographies called ''central collineations''. It is a part of the fundamental theorem of projective geometry that the two definitions are equivalent.

In a projective space, ''P'', of dimension , a collineation of ''P'' is a bijection from ''P'' onto ''P'' that maps lines onto lines. A central collineation (traditionally these were called ''perspectivities'', but this term may be confusing, having another meaning; see Perspectivity) is a bijection ''α'' from ''P'' to ''P'', such that there exists a hyperplane ''H'' (called the ''axis'' of ''α''), which is fixed pointwise by ''α'' (that is, for all points ''X'' in ''H'') and a point ''O'' (called the ''center'' of ''α''), which is fixed linewise by ''α'' (any line through ''O'' is mapped to itself by ''α'', but not necessarily pointwise). There are two types of central collineations. Elations are the central collineations in which the center is incident with the axis and homologies are those in which the center is not incident with the axis. A central collineation is uniquely defined by its center, its axis, and the image ''α''(''P'') of any given point ''P'' that differs from the center ''O'' and does not belong to the axis. (The image ''α''(''Q'') of any other point ''Q'' is the intersection of the line defined by ''O'' and ''Q'' and the line passing through ''α''(''P'') and the intersection with the axis of the line defined by ''P'' and ''Q''.)

A central collineation is a homography defined by a (''n''+1) × (''n''+1) matrix that has an eigenspace of dimension ''n''. It is a homology, if the matrix has another eigenvalue and is therefore diagonalizable. It is an elation, if all the eigenvalues are equal and the matrix is not diagonalizable.

The geometric view of a central collineation is easiest to see in a projective plane. Given a central collineation α, consider a line $\ell$ that does not pass through the center ''O'', and its image under ''α'', $\ell ' = \alpha(\ell)$. Setting $R = \ell \cap \ell '$, the axis of ''α'' is some line ''M'' through ''R''. The image of any point ''A'' of $\ell$ under ''α'' is the intersection of ''OA'' with $\ell '$. The image ''B''′ of a point ''B'' that does not belong to $\ell$ may be constructed in the following way: let $S= AB\cap M$, then $B'=SA'\cap OB$.

The composition of two central collineations, while still a homography in general, is not a central collineation. In fact, every homography is the composition of a finite number of central collineations. In synthetic geometry, this property, which is a part of the fundamental theory of projective geometry is taken as the definition of homographies.

Fundamental theorem of projective geometry

There are collineations besides the homographies. In particular, any field automorphism ''σ'' of a field ''F'' induces a collineation of every projective space over ''F'' by applying ''σ'' to all homogeneous coordinates (over a projective frame) of a point. These collineations are called automorphic collineations.

The fundamental theorem of projective geometry consists of the three following theorems.
# Given two projective frames of a projective space ''P'', there is exactly one homography of ''P'' that maps the first frame onto the second one.
# If the dimension of a projective space ''P'' is at least two, every collineation of ''P'' is the composition of an automorphic collineation and a homography. In particular, over the reals, every collineation of a projective space of dimension at least two is a homography.
# Every homography is the composition of a finite number of perspectivities. In particular, if the dimension of the implied projective space is at least two, every homography is the composition of a finite number of central collineations.

If projective spaces are defined by means of axioms ( synthetic geometry), the third part is simply a definition. On the other hand, if projective spaces are defined by means of linear algebra, the first part is an easy corollary of the definitions. Therefore, the proof of the first part in synthetic geometry, and the proof of the third part in terms of linear algebra both are fundamental steps of the proof of the equivalence of the two ways of defining projective spaces.

Homography groups

As every homography has an inverse mapping and the composition of two homographies is another, the homographies of a given projective space form a group. For example, the Möbius group is the homography group of any complex projective line.

As all the projective spaces of the same dimension over the same field are isomorphic, the same is true for their homography groups. They are therefore considered as a single group acting on several spaces, and only the dimension and the field appear in the notation, not the specific projective space.

Homography groups also called projective linear groups are denoted when acting on a projective space of dimension ''n'' over a field ''F''. Above definition of homographies shows that may be identified to the quotient group , where is the general linear group of the invertible matrices, and ''F''^×''I'' is the group of the products by a nonzero element of ''F'' of the identity matrix of size .

When ''F'' is a Galois field GF(''q'') then the homography group is written . For example, acts on the eight points in the projective line over the finite field GF(7), while , which is isomorphic to the alternating group A₅, is the homography group of the projective line with five points.

The homography group is a subgroup of the ''collineation group'' of the collineations of a projective space of dimension ''n''. When the points and lines of the projective space are viewed as a block design, whose blocks are the sets of points contained in a line, it is common to call the collineation group the ''automorphism group of the design''.

Cross-ratio

The cross-ratio of four collinear points is an invariant under the homography that is fundamental for the study of the homographies of the lines.

Three distinct points , and on a projective line over a field form a projective frame of this line. There is therefore a unique homography of this line onto that maps to , to 0, and to 1. Given a fourth point on the same line, the cross-ratio of the four points , , and , denoted , is the element of . In other words, if has homogeneous coordinates over the projective frame , then .

Over a ring

Suppose ''A'' is a ring and ''U'' is its group of units. Homographies act on a projective line over ''A'', written P(''A''), consisting of points with projective coordinates. The homographies on P(''A'') are described by matrix mappings
:U ,1begina & c \\ b & d \end = U a + b, \ zc + d.
When ''A'' is a commutative ring, the homography may be written
:$z \mapsto \frac \ ,$
but otherwise the linear fractional transformation is seen as an equivalence:
:U a + b,\ zc + d\thicksim U z c + d)^ (z a + b),\ 1

The homography group of the ring of integers Z is modular group . Ring homographies have been used in quaternion analysis, and with dual quaternions to facilitate screw theory. The conformal group of spacetime can be represented with homographies where ''A'' is the composition algebra of biquaternions.

Periodic homographies

The homography $h = \begin1 & 1 \\ 0 & 1 \end$ is periodic when the ring is Z/''n''Z (the integers modulo ''n'') since then
$h^n = \begin1 & n \\ 0 & 1 \end = \begin1 & 0 \\ 0 & 1 \end .$
Arthur Cayley was interested in periodicity when he calculated iterates in 1879.
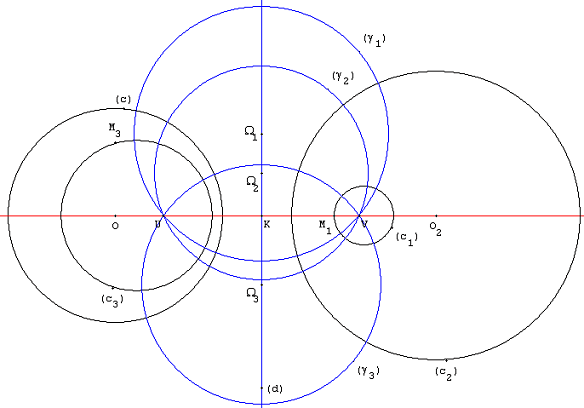
In his review of a brute force approach to periodicity of homographies, H. S. M. Coxeter gave this analysis:
:A real homography is involutory (of period 2) if and only if . If it is periodic with period , then it is elliptic, and no loss of generality occurs by assuming that . Since the characteristic roots are exp(±''hπi''/''m''), where , the trace is .
H. S. M. Coxeter
On periodicity
in Mathematical Reviews

See also

* W-curve

Notes

References

*
*
*, translated from the 1977 French original by M. Cole and S. Levy, fourth printing of the 1987 English translation
*
*
*
*
*

Further reading

*Patrick du Val (1964) ''Homographies, quaternions and rotations'', Oxford Mathematical Monographs, Clarendon Press, Oxford, .
*Gunter Ewald (1971) ''Geometry: An Introduction'', page 263, Belmont: Wadsworth Publishing .

External links

*{{Commonscatinline

Projective geometry
Transformation (function)