In mathematics, the curve-shortening flow is a process that modifies a

smooth curve In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight. Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that ...

in the

Euclidean plane In mathematics, the Euclidean plane is a Euclidean space of dimension two. That is, a geometric setting in which two real quantities are required to determine the position of each point ( element of the plane), which includes affine notions ...

by moving its points perpendicularly to the curve at a speed proportional to the

curvature In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane. For curves, the cano ...

. The curve-shortening flow is an example of a geometric flow, and is the one-dimensional case of the

mean curvature flow In the field of differential geometry in mathematics, mean curvature flow is an example of a geometric flow of hypersurfaces in a Riemannian manifold (for example, smooth surfaces in 3-dimensional Euclidean space). Intuitively, a family of sur ...

. Other names for the same process include the Euclidean shortening flow, geometric heat flow, and arc length evolution. As the points of any smooth

simple closed curve In topology, the Jordan curve theorem asserts that every ''Jordan curve'' (a plane simple closed curve) divides the plane into an "interior" region bounded by the curve and an " exterior" region containing all of the nearby and far away exterior ...

move in this way, the curve remains simple and smooth. It loses area at a constant rate, and its perimeter decreases as quickly as possible for any continuous curve evolution. If the curve is non-convex, its

total absolute curvature In differential geometry, the total absolute curvature of a smooth curve is a number defined by integrating the absolute value of the curvature around the curve. It is a dimensionless quantity that is invariant under similarity transformations of t ...

decreases monotonically, until it becomes convex. Once convex, the isoperimetric ratio of the curve decreases as the curve converges to a circular shape, before collapsing to a single point of singularity. If two disjoint simple smooth closed curves evolve, they remain disjoint until one of them collapses to a point. The circle is the only simple closed curve that maintains its shape under the curve-shortening flow, but some curves that cross themselves or have infinite length keep their shape, including the grim reaper curve, an infinite curve that translates upwards, and

spiral In mathematics, a spiral is a curve which emanates from a point, moving farther away as it revolves around the point. Helices Two major definitions of "spiral" in the American Heritage Dictionary are:polygon In geometry, a polygon () is a plane figure that is described by a finite number of straight line segments connected to form a closed '' polygonal chain'' (or ''polygonal circuit''). The bounded plane region, the bounding circuit, or the two t ...

and using the

finite difference method In numerical analysis, finite-difference methods (FDM) are a class of numerical techniques for solving differential equations by approximating derivatives with finite differences. Both the spatial domain and time interval (if applicable) are ...

to calculate the motion of each polygon vertex. Alternative methods include computing a

convolution In mathematics (in particular, functional analysis), convolution is a mathematical operation on two functions ( and ) that produces a third function (f*g) that expresses how the shape of one is modified by the other. The term ''convolution'' ...

of polygon vertices and then resampling vertices on the resulting curve, or repeatedly applying a

median filter The median filter is a non-linear digital filtering technique, often used to remove noise from an image or signal. Such noise reduction is a typical pre-processing step to improve the results of later processing (for example, edge detection on an ...

to a

digital image A digital image is an image composed of picture elements, also known as ''pixels'', each with ''finite'', '' discrete quantities'' of numeric representation for its intensity or gray level that is an output from its two-dimensional functions f ...

whose black and white pixels represent the inside and outside of the curve. The curve-shortening flow was originally studied as a model for annealing of metal sheets. Later, it was applied in image analysis to give a multi-scale representation of shapes. It can also model

reaction–diffusion system Reaction–diffusion systems are mathematical models which correspond to several physical phenomena. The most common is the change in space and time of the concentration of one or more chemical substances: local chemical reactions in which the s ...

s, and the behavior of

cellular automata A cellular automaton (pl. cellular automata, abbrev. CA) is a discrete model of computation studied in automata theory. Cellular automata are also called cellular spaces, tessellation automata, homogeneous structures, cellular structures, tessel ...

. The curve-shortening flow can be used to find

closed geodesic In differential geometry and dynamical systems, a closed geodesic on a Riemannian manifold is a geodesic that returns to its starting point with the same tangent direction. It may be formalized as the projection of a closed orbit of the geodesic fl ...

s on

Riemannian manifold In differential geometry, a Riemannian manifold or Riemannian space , so called after the German mathematician Bernhard Riemann, is a real, smooth manifold ''M'' equipped with a positive-definite inner product ''g'p'' on the tangent space ' ...

s, and as a model for the behavior of higher-dimensional flows.

Definitions

A flow is a process in which the points of a space continuously change their locations or properties over time. More specifically, in a one-dimensional geometric flow such as the curve-shortening flow, the points undergoing the flow belong to a

curve In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight. Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that ...

, and what changes is the shape of the curve, its

embedding In mathematics, an embedding (or imbedding) is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup. When some object X is said to be embedded in another object Y, the embedding is gi ...

into the Euclidean plane determined by the locations of each of its points. In the curve-shortening flow, each point of a curve moves in the direction of a

normal vector In geometry, a normal is an object such as a line, ray, or vector that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the (infinite) line perpendicular to the tangent line to the curve ...

to the curve, at a rate proportional to the

. For an evolving curve represented by a two-parameter function where parameterizes the arc length along the curve and parameterizes a time in the evolution of the curve, the curve-shortening flow can be described by the

parabolic partial differential equation A parabolic partial differential equation is a type of partial differential equation (PDE). Parabolic PDEs are used to describe a wide variety of time-dependent phenomena, including heat conduction, particle diffusion, and pricing of derivati ...

\frac = \frac = \kappa n,

a form of the

heat equation In mathematics and physics, the heat equation is a certain partial differential equation. Solutions of the heat equation are sometimes known as caloric functions. The theory of the heat equation was first developed by Joseph Fourier in 1822 for t ...

, where is the curvature and is the unit normal vector. Because the ingredients of this equation, the arc length, curvature, and time, are all unaffected by translations and rotations of the Euclidean plane, it follows that the flow defined by this equation is invariant under translations and rotations (or more precisely,

equivariant In mathematics, equivariance is a form of symmetry for functions from one space with symmetry to another (such as symmetric spaces). A function is said to be an equivariant map when its domain and codomain are acted on by the same symmetry group, ...

). If the plane is scaled by a constant dilation factor, the flow remains essentially unchanged, but is slowed down or sped up by the same factor.

Non-smooth curves

In order for the flow to be well defined, the given curve must be sufficiently smooth that it has a continuous curvature. However, once the flow starts, the curve becomes analytic, and remains so until reaching a singularity at which the curvature blows up. For a smooth curve without crossings, the only possible singularity happens when the curve collapses to a point, but immersed curves can have other types of singularity. In such cases, with some care it is possible to continue the flow past these singularities until the whole curve shrinks to a single point. For a simple closed curve, using an extension of the flow to non-smooth curves based on the

level-set method Level-set methods (LSM) are a conceptual framework for using level sets as a tool for numerical analysis of surfaces and shapes. The advantage of the level-set model is that one can perform numerical computations involving curves and surfaces on a ...

, there are only two possibilities. Curves with zero

Lebesgue measure In measure theory, a branch of mathematics, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of ''n''-dimensional Euclidean space. For ''n'' = 1, 2, or 3, it coincides ...

(including all

polygon In geometry, a polygon () is a plane figure that is described by a finite number of straight line segments connected to form a closed '' polygonal chain'' (or ''polygonal circuit''). The bounded plane region, the bounding circuit, or the two t ...

s and piecewise-smooth curves) instantly evolve into smooth curves, after which they evolve as any smooth curve would. However, Osgood curves with nonzero measure instead immediately evolve into a topological annulus with nonzero area and smooth boundaries. The

topologist's sine curve In the branch of mathematics known as topology, the topologist's sine curve or Warsaw sine curve is a topological space with several interesting properties that make it an important textbook example. It can be defined as the graph of the functi ...

is an example that instantly becomes smooth, despite not even being

locally connected In topology and other branches of mathematics, a topological space ''X'' is locally connected if every point admits a neighbourhood basis consisting entirely of open, connected sets. Background Throughout the history of topology, connectedness ...

; examples such as this show that the reverse evolution of the curve-shortening flow can take well-behaved curves to complicated singularities in a finite amount of time.

Non-Euclidean surfaces

The curve-shortening flow, and many of the results about the curve-shortening flow, can be generalized from the Euclidean plane to any two-dimensional

. In order to avoid additional types of singularity, it is important for the manifold to be ''convex at infinity''; this is defined to mean that every

compact set In mathematics, specifically general topology, compactness is a property that seeks to generalize the notion of a closed and bounded subset of Euclidean space by making precise the idea of a space having no "punctures" or "missing endpoints", ...

has a compact

convex hull In geometry, the convex hull or convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean spac ...

, as defined using

geodesic convexity In mathematics — specifically, in Riemannian geometry — geodesic convexity is a natural generalization of convexity for sets and functions to Riemannian manifolds. It is common to drop the prefix "geodesic" and refer simply to "convexi ...

. The curve-shortening flow cannot cause a curve to depart from its convex hull, so this condition prevents parts of the curve from reaching the boundary of the manifold.

Space curves

The curve-shortening flow has also been studied for curves in three-dimensional

Euclidean space Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean ...

. The normal vector in this case can be defined (as in the plane) as the derivative of the tangent vector with respect to arc length, normalized to be a unit vector; it is one of the components of the Frenet–Serret frame. It is not well defined at points of zero curvature, but the product of the curvature and the normal vector remains well defined at those points, allowing the curve-shortening flow to be defined. Curves in space may cross each other or themselves according to this flow, and the flow may lead to singularities in the curves; every singularity is asymptotic to a plane. However, spherical curves and curves which can be orthogonally projected into a regular convex planar curve are known to remain simple. The curve shortening flow for space curves has been used as a way to define flow past singularities in plane curves.

Beyond curves

It is possible to extend the definition of the flow to more general inputs than curves, for instance by using rectifiable varifolds or the

. However, these extended definitions may allow parts of curves to vanish instantaneously or fatten into sets of nonzero area. Curve-shortening ambiguity

A commonly studied variation of the problem involves networks of interior-disjoint smooth curves, with junctions where three or more of the curves meet. When the junctions all have exactly three curves meeting at angles of 2/3 (the same conditions seen in an optimal

Steiner tree In combinatorial mathematics, the Steiner tree problem, or minimum Steiner tree problem, named after Jakob Steiner, is an umbrella term for a class of problems in combinatorial optimization. While Steiner tree problems may be formulated in a nu ...

or two-dimensional

foam Foams are materials formed by trapping pockets of gas in a liquid or solid. A bath sponge and the head on a glass of beer are examples of foams. In most foams, the volume of gas is large, with thin films of liquid or solid separating the ...

soap bubble A soap bubble is an extremely thin film of soap or detergent and water enclosing air that forms a hollow sphere with an iridescent surface. Soap bubbles usually last for only a few seconds before bursting, either on their own or on contact w ...

s) the flow is well-defined for the short term. However, it may eventually reach a singular state with four or more curves meeting at a junction, and there may be more than one way to continue the flow past such a singularity.

Behavior

Avoidance principle, radius, and stretch factor

If two disjoint smooth simple closed curves undergo the curve-shortening flow simultaneously, they remain disjoint as the flow progresses. The reason is that, if two smooth curves move in a way that creates a crossing, then at the time of first crossing the curves would necessarily be tangent to each other, without crossing. But, in such a situation, the two curves' curvatures at the point of tangency would necessarily pull them apart rather than pushing them together into a crossing. For the same reason, a single simple closed curve can never evolve to cross itself. This phenomenon is known as the avoidance principle. The avoidance principle implies that any smooth closed curve must eventually reach a singularity, such as a point of infinite curvature. For, if a given smooth curve is surrounded by a circle, both will remain disjoint for as long as they both exist. But the enclosing circle shrinks under the curvature flow, remaining circular, until it collapses, and by the avoidance principle must remain contained within it. So, if were to never reach a singularity, it would be trapped at a single point at the time when the circle collapses, which is impossible for a smooth curve. This can be quantified by observing that the radius of the smallest circle that encloses must decrease at a rate that is at least as fast as the decrease in radius of a circle undergoing the same flow. quantifies the avoidance principle for a single curve in terms of the ratio between the arc length (of the shorter of two arcs) and Euclidean distance between pairs of points, sometimes called the

stretch factor The stretch factor (i.e., bilipschitz constant) of an embedding measures the factor by which the embedding distorts distances. Suppose that one metric space is embedded into another metric space by a metric map, a continuous one-to-one funct ...

. He shows that the stretch factor is strictly decreasing at each of its local maxima, except for the case of the two ends of a diameter of a circle in which case the stretch factor is constant at . This monotonicity property implies the avoidance principle, for if the curve would ever touch itself the stretch factor would become infinite at the two touching points.

Length

As a curve undergoes the curve-shortening flow, its

length Length is a measure of distance. In the International System of Quantities, length is a quantity with dimension distance. In most systems of measurement a base unit for length is chosen, from which all other units are derived. In the In ...

decreases at a rate given by the formula :

\frac = -\int \kappa^2 \, ds,

where the integral is taken over the curve, is the curvature, and is arc length along the curve. The integrand is always non-negative, and for any smooth closed curve there exist arcs within which it is strictly positive, so the length decreases monotonically. More generally, for any evolution of curves whose normal speed is , the rate of change in length is :

\frac = -\int f\kappa \, ds,

which can be interpreted as a negated

inner product In mathematics, an inner product space (or, rarely, a Hausdorff pre-Hilbert space) is a real vector space or a complex vector space with an operation called an inner product. The inner product of two vectors in the space is a scalar, often de ...

between the given evolution and the curve-shortening flow. Thus, the curve-shortening flow can be described as the gradient flow for length, the flow that (locally) decreases the length of the curve as quickly as possible relative to the norm of the flow. This property is the one that gives the curve-shortening flow its name.

Area

For a simple closed curve, the

area Area is the quantity that expresses the extent of a region on the plane or on a curved surface. The area of a plane region or ''plane area'' refers to the area of a shape or planar lamina, while '' surface area'' refers to the area of an open ...

enclosed by the curve shrinks, at the constant rate of 2 units of area per unit of time, independent of the curve. Therefore, the total time for a curve to shrink to a point is proportional to its area, regardless of its initial shape. Because the area of a curve is reduced at a constant rate, and (by the

isoperimetric inequality In mathematics, the isoperimetric inequality is a geometric inequality involving the perimeter of a set and its volume. In n-dimensional space \R^n the inequality lower bounds the surface area or perimeter \operatorname(S) of a set S\subset\R^n b ...

) a circle has the greatest possible area among simple closed curves of a given length, it follows that circles are the slowest curves to collapse to a point under the curve-shortening flow. All other curves take less time to collapse than a circle of the same length. The constant rate of area reduction is the only

conservation law In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves over time. Exact conservation laws include conservation of energy, conservation of linear momentum, ...

satisfied by the curve-shortening flow. This implies that it is not possible to express the "vanishing point" where the curve eventually collapses as an integral over the curve of any function of its points and their derivatives, because such an expression would lead to a forbidden second conservation law. However, by combining the constant rate of area loss with the avoidance principle, it is possible to prove that the vanishing point always lies within a circle, concentric with the minimum enclosing circle, whose area is the difference in areas between the enclosing circle and the given curve.

Total absolute curvature

The

of a smooth curve is the integral of the

absolute value In mathematics, the absolute value or modulus of a real number x, is the non-negative value without regard to its sign. Namely, , x, =x if is a positive number, and , x, =-x if x is negative (in which case negating x makes -x positive), an ...

of the curvature along the arc length of the curve, :

K=\int, \kappa,  \,ds.

It can also be expressed as a sum of the angles between the normal vectors at consecutive pairs of

inflection point In differential calculus and differential geometry, an inflection point, point of inflection, flex, or inflection (British English: inflexion) is a point on a smooth plane curve at which the curvature changes sign. In particular, in the case o ...

s. It is 2 for convex curves and larger for non-convex curves, serving as a measure of non-convexity of a curve. New inflection points cannot be created by the curve-shortening flow. Each of the angles in the representation of the total absolute curvature as a sum decreases monotonically, except at the instants when two consecutive inflection points reach the same angle or position as each other and are both eliminated. Therefore, the total absolute curvature can never increase as the curve evolves. For convex curves it is constant at 2 and for non-convex curves it decreases monotonically.

Gage–Hamilton–Grayson theorem

If a smooth simple closed curve undergoes the curve-shortening flow, it remains smoothly embedded without self-intersections. It will eventually become

convex Convex or convexity may refer to: Science and technology * Convex lens, in optics Mathematics * Convex set, containing the whole line segment that joins points ** Convex polygon, a polygon which encloses a convex set of points ** Convex polyto ...

, and once it does so it will remain convex. After this time, all points of the curve will move inwards, and the shape of the curve will converge to a

circle A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is con ...

as the whole curve shrinks to a single point. This behavior is sometimes summarized by saying that every simple closed curve shrinks to a "round point". This result is due to Michael Gage, Richard S. Hamilton, and Matthew Grayson. proved convergence to a circle for convex curves that contract to a point. More specifically Gage showed that the isoperimetric ratio (the ratio of squared curve length to area, a number that is 4 for a circle and larger for any other convex curve) decreases monotonically and quickly. proved that all smooth convex curves eventually contract to a point without forming any other singularities, and proved that every non-convex curve will eventually become convex. provide a simpler proof of Grayson's result, based on the monotonicity of the stretch factor. Curve-shortening self-similar lens

Similar results can be extended from closed curves to unbounded curves satisfying a local Lipschitz condition. For such curves, if both sides of the curve have infinite area, then the evolved curve remains smooth and singularity-free for all time. However, if one side of an unbounded curve has finite area, and the curve has finite total absolute curvature, then its evolution reaches a singularity in time proportional to the area on the finite-area side of the curve, with unbounded curvature near the singularity. For curves that are graphs of sufficiently well-behaved functions, asymptotic to a ray in each direction, the solution converges in shape to a unique shape that is asymptotic to the same rays. For networks formed by two disjoint rays on the same line, together with two smooth curves connecting the endpoints of the two rays, an analogue of the Gage–Hamilton–Grayson theorem holds, under which the region between the two curves becomes convex and then converges to a

vesica piscis The vesica piscis is a type of lens, a mathematical shape formed by the intersection of two disks with the same radius, intersecting in such a way that the center of each disk lies on the perimeter of the other. In Latin, "vesica piscis" litera ...

shape.

Singularities of self-crossing curves

Curves that have self-crossings may reach singularities before contracting to a point. For instance, if a

lemniscate In algebraic geometry, a lemniscate is any of several figure-eight or -shaped curves. The word comes from the Latin "''lēmniscātus''" meaning "decorated with ribbons", from the Greek λημνίσκος meaning "ribbons",. or which alternativel ...

(any smooth immersed curve with a single crossing, resembling a figure 8 or

infinity symbol The infinity symbol (\infty) is a mathematical symbol representing the concept of infinity. This symbol is also called a lemniscate, after the lemniscate curves of a similar shape studied in algebraic geometry, or "lazy eight", in the termi ...

) has unequal areas in its two lobes, then eventually the smaller lobe will collapse to a point. However, if the two lobes have equal areas, then they will remain equal throughout the evolution of the curve, and the isoperimetric ratio will diverge as the curve collapses to a singularity. When a locally convex self-crossing curve approaches a singularity as one of its loops shrinks, it either shrinks in a self-similar way or asymptotically approaches the grim reaper curve (described below) as it shrinks. When a loop collapses to a singularity, the amount of total absolute curvature that is lost is either at least 2 or exactly .

On Riemannian manifolds

On a Riemannian manifold, any smooth simple closed curve will remain smooth and simple as it evolves, just as in the Euclidean case. It will either collapse to a point in a finite amount of time, or remain smooth and simple forever. In the latter case, the curve necessarily converges to a

of the surface. Immersed curves on Riemannian manifolds, with finitely many self-crossings, become self-tangent only at a discrete set of times, at each of which they lose a crossing. As a consequence the number of self-crossing points is non-increasing. PelotaTenis

Curve shortening on a

sphere A sphere () is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. A sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the ...

can be used as part of a proof of the

tennis ball theorem In geometry, the tennis ball theorem states that any smooth curve on the surface of a sphere that divides the sphere into two equal-area subsets without touching or crossing itself must have at least four inflection points, points at which the cur ...

. This theorem states that every smooth simple closed curve on the sphere that divides the sphere's surface into two equal areas (like the seam of a

tennis ball A tennis ball is a ball designed for the sport of tennis. Tennis balls are fluorescent yellow in organised competitions, but in recreational play can be virtually any color. Tennis balls are covered in a fibrous felt which modifies their aerodyna ...

) must have at least four

s. The proof comes from the observation that curve shortening preserves the smoothness and area-bisection properties of the curve, and does not increase its number of inflection points. Therefore, it allows the problem to be reduced to the problem for curves near the limiting shape of curve shortening, a

great circle In mathematics, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere's center point. Any arc of a great circle is a geodesic of the sphere, so that great circles in spherical geometry ...

Huisken's monotonicity formula

According to Huisken's monotonicity formula, the convolution of an evolving curve with a time-reversed

heat kernel In the mathematical study of heat conduction and diffusion, a heat kernel is the fundamental solution to the heat equation on a specified domain with appropriate boundary conditions. It is also one of the main tools in the study of the spectrum o ...

is non-increasing. This result can be used to analyze the singularities of the evolution.

Specific curves

Curves with self-similar evolution

Because every other simple closed curve converges to a circle, the circle is the only simple closed curve that keeps its shape under the curve-shortening flow. However, there are many other examples of curves that are either non-simple (they include self-crossings) or non-closed (they extend to infinity) and keep their shape. In particular,; ; ; , "2. Invariant solutions for the curve-shortening flow", pp. 27–44; ; . * Every

line Line most often refers to: * Line (geometry), object with zero thickness and curvature that stretches to infinity * Telephone line, a single-user circuit on a telephone communication system Line, lines, The Line, or LINE may also refer to: Art ...

stays unchanged by the curve-shortening flow. Lines are the only curves that are unaffected by the curve-shortening flow, although there exist more complex stable networks of curves, such as the

hexagonal tiling In geometry, the hexagonal tiling or hexagonal tessellation is a regular tiling of the Euclidean plane, in which exactly three hexagons meet at each vertex. It has Schläfli symbol of or (as a truncated triangular tiling). English mathemati ...

of the plane. * The grim reaper curve moves upwards without changing its shape. In the same way, any curve similar to the grim reaper is

translated Translation is the communication of the meaning of a source-language text by means of an equivalent target-language text. The English language draws a terminological distinction (which does not exist in every language) between ''transl ...

by the curve-shortening flow, shifted in the direction of the

symmetry axis Rotational symmetry, also known as radial symmetry in geometry, is the property a shape has when it looks the same after some rotation by a partial turn. An object's degree of rotational symmetry is the number of distinct orientations in which ...

of the curve without changing its shape or orientation. The grim reaper is the only curve with this property. It is also called the ''hairpin model'' in the physics literature. * A family of self-crossing closed curves, derived from projections of

torus knot In knot theory, a torus knot is a special kind of knot that lies on the surface of an unknotted torus in R3. Similarly, a torus link is a link which lies on the surface of a torus in the same way. Each torus knot is specified by a pair of co ...

s, shrink homothetically but remain self-similar under the curve-shortening flow. These have come to be known as the Abresch–Langer curves, after the work of , although they were mentioned earlier by and rediscovered independently by . These curves are locally convex, and therefore can be described by their support functions. Suitably scaled versions of these support functions obey the

differential equation In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, a ...

h''+h=\frac,

:which has positive periodic solutions (corresponding to curves with self-similar evolution) for any period that is strictly between and

\pi\sqrt

. * Other curves, including some infinite

spiral In mathematics, a spiral is a curve which emanates from a point, moving farther away as it revolves around the point. Helices Two major definitions of "spiral" in the American Heritage Dictionary are: * For networks of smooth curves, meeting in threes at junctions with angles of 2/3, the self-similar shrinking solutions include a double bubble surrounding two equal areas, a

lens A lens is a transmissive optical device which focuses or disperses a light beam by means of refraction. A simple lens consists of a single piece of transparent material, while a compound lens consists of several simple lenses (''elements'' ...

shape (

) bounded by two congruent arcs of circles together with two collinear rays having their apexes at the corners of the lens, and a "fish-shaped" network bounded by a line segment, two rays, and a convex curve. Any other self-similar shrinking networks involve a larger number of curves. Another family of networks grows homothetically and remains self-similar; these are tree-like networks of curves, meeting at angles of 2/3 at triple junctions,

asymptotic In analytic geometry, an asymptote () of a curve is a line such that the distance between the curve and the line approaches zero as one or both of the ''x'' or ''y'' coordinates tends to infinity. In projective geometry and related contexts, ...

to a fan of two or more rays that meet at a common endpoint. The two-ray case of these shapes is an unbounded smooth curve; for three or more rays the evolution of these shapes may be defined using generalized variants of the curve-shortening flow such as the one for varifolds. A given fan of four or more rays may be asymptotic to more than one different solution of this type, so these solutions do not provide a unique definition for the curve-shortening flow starting from a fan of rays.

Ancient solutions

An ancient solution to a flow problem is a curve whose evolution can be extrapolated backwards for all time, without singularities. All of the self-similar solutions that shrink or stay the same size rather than growing are ancient solutions in this sense; they can be extrapolated backwards by reversing the

self-similarity __NOTOC__ In mathematics, a self-similar object is exactly or approximately similar to a part of itself (i.e., the whole has the same shape as one or more of the parts). Many objects in the real world, such as coastlines, are statistically s ...

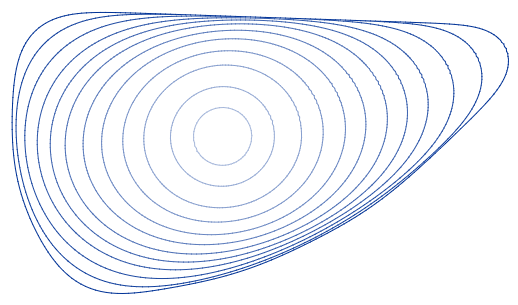
transformation that they would undergo by the forwards curve-shortening flow. Thus, for instance, the circle, grim reaper, and Abresch–Langer curves are all ancient solutions. There are also examples which are not self-similar. An explicit example is the Angenent oval solution after the work of . This family of curves may be parameterized by specifying the curvature as a function of the tangent angle using the formula :

k(\theta,t)=\sqrt

and have as their limiting shape under reverse evolution a pair of grim reaper curves approaching each other from opposite directions. In the

Cartesian coordinate system A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured i ...

, they may be given by the

implicit curve In mathematics, an implicit curve is a plane curve defined by an implicit equation relating two coordinate variables, commonly ''x'' and ''y''. For example, the unit circle is defined by the implicit equation x^2+y^2=1. In general, every impli ...

equation :

\cosh y - e^\cos x = 0.

In the physics literature, the same shapes are known as the ''paperclip model''.; . The Angenent oval and shrinking circle solutions are the only ancient solutions whose timeslices bound bounded convex sets. The Grim Reaper, stationary halfspace and stationary strip solutions are the only examples whose timeslices bound unbounded convex sets. There exist many further (nonembedded) ''locally'' convex examples as well as many further (nonconvex) embedded examples.

Numerical approximations

In order to compute the curve-shortening flow efficiently, both a continuous curve and the continuous evolution of the curve need to be replaced by a discrete approximation.

Front tracking

Front tracking methods have long been used in

fluid dynamics In physics and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids— liquids and gases. It has several subdisciplines, including ''aerodynamics'' (the study of air and other gases in motion) an ...

to model and track the motion of boundaries between different materials, of steep gradients in material properties such as

weather front A weather front is a boundary separating air masses for which several characteristics differ, such as air density, wind, temperature, and humidity. Disturbed and unstable weather due to these differences often arises along the boundary. For ...

s, or of shock waves within a single material. These methods involve deriving the equations of motion of the boundary, and using them to directly simulate the motion of the boundary, rather than simulating the underlying fluid and treating the boundary as an emergent property of the fluid. The same methods can also be used to simulate the curve-shortening flow, even when the curve undergoing the flow is not a boundary or shock. In front tracking methods for curve shortening, the curve undergoing the evolution is discretized as a polygon. The

is used to derive formulas for the approximate normal vector and curvature at each vertex of the polygon, and these values are used to determine how to move each vertex in each time step. Although the curve-shortening flow is defined by the motion of a curve perpendicularly to itself, some parameterizations of the curve-shortening flow may allow the vertices that approximate the curve to move non-perpendicularly. In effect, this allows the vertices to move along the curve, as the curve evolves. Choosing a careful reparameterization can help redistribute the vertices more evenly along the curve in situations where perpendicular motion would cause them to bunch up. write that these methods are fast and accurate but that it is much more complicated to extend them to versions of the curve-shortening flow that apply to more complicated inputs than simple closed curves, where it is necessary to deal with singularities and changes of topology. For most such methods, warns that "The conditions of stability cannot be determined easily and the time step must be chosen ad hoc." Another finite differencing method by modifies the formula for the curvature at each vertex by adding to it a small term based on the

Laplace operator In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean space. It is usually denoted by the symbols \nabla\cdot\nabla, \nabla^2 (where \nabla is the ...

. This modification is called elliptic regularization, and it can be used to help prove the existence of generalized flows as well as in their numerical simulation. Using it, the method of Crandall and Lions can be proven to converge and is the only numerical method listed by Cao that is equipped with bounds on its convergence rate. For an empirical comparison of the forward Euler, backward Euler, and more accurate Crank–Nicolson finite difference methods, see .

Resampled convolution

suggest a numerical method for computing an approximation to the curve-shortening flow that maintains a discrete approximation to the curve and alternates between two steps: * Resample the current curve by placing new sample points at a uniform spacing, as measured by normalized arc length. * Convolve the locations of the points with a

Gaussian function In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function of the base form f(x) = \exp (-x^2) and with parametric extension f(x) = a \exp\left( -\frac \right) for arbitrary real constants , and non-zero . It is ...

with small standard deviation, in effect replacing each point's location with a

weighted average The weighted arithmetic mean is similar to an ordinary arithmetic mean (the most common type of average), except that instead of each of the data points contributing equally to the final average, some data points contribute more than others. The ...

of the locations of nearby points along the curve, with Gaussian weights. The standard deviation of the Gaussian should be chosen to be small enough that, after this step, the sample points still have nearly-uniform spacing. As they show, this method converges to the curve-shortening distribution in the limit as the number of sample points grows and the normalized arc length of the convolution radius shrinks.

Median filtering

describe a scheme operating on a two-dimensional square grid – effectively an array of

pixel In digital imaging, a pixel (abbreviated px), pel, or picture element is the smallest addressable element in a raster image, or the smallest point in an all points addressable display device. In most digital display devices, pixels are the sma ...

s. The curve to be evolved is represented by assigning the value 0 (black) to pixels exterior to the curve, and 1 (white) to pixels interior to the curve, giving the

indicator function In mathematics, an indicator function or a characteristic function of a subset of a set is a function that maps elements of the subset to one, and all other elements to zero. That is, if is a subset of some set , one has \mathbf_(x)=1 if x\i ...

for the interior of the curve. This representation is updated by alternating two steps: * Convolve the pixelated image with a

to simulate its evolution under the

for a short time step. The result is a

Gaussian blur In image processing, a Gaussian blur (also known as Gaussian smoothing) is the result of blurring an image by a Gaussian function (named after mathematician and scientist Carl Friedrich Gauss). It is a widely used effect in graphics software, ...

of the image, or equivalently the

Weierstrass transform In mathematics, the Weierstrass transform of a function , named after Karl Weierstrass, is a "smoothed" version of obtained by averaging the values of , weighted with a Gaussian centered at ''x''. Specifically, it is the function defined ...

of the indicator function, with radius proportional to the square root of the time step. * Set every pixel with numerical value less than 1/2 to 0, and every pixel with numerical value greater than 1/2 to 1, thresholding the image back to its original values in new positions. In order for this scheme to be accurate, the time step must be large enough to cause the curve to move by at least one pixel even at points of low curvature, but small enough to cause the radius of blurring to be less than the minimum radius of curvature. Therefore, the size of a pixel must be , small enough to allow a suitable intermediate time step to be chosen. The method can be generalized to the evolution of networks of curves, meeting at junctions and dividing the plane into more than three regions, by applying the same method simultaneously to each region. Instead of blurring and thresholding, this method can alternatively be described as applying a

with

Gaussian Carl Friedrich Gauss (1777–1855) is the eponym of all of the topics listed below. There are over 100 topics all named after this German mathematician and scientist, all in the fields of mathematics, physics, and astronomy. The English eponymo ...

weights to each pixel. It is possible to use kernels other than the heat kernel, or to adaptively refine the grid so that it has high resolution near the curve but does not waste time and memory on pixels far from the curve that do not contribute to the outcome. Instead of using only the two values in the pixelated image, a version of this method that uses an image whose pixel values represent the signed distance to the curve can achieve subpixel accuracy and require lower resolution.

Applications

Annealing metal sheets

An early reference to the curve-shortening flow by motivates it as a model for the physical process of annealing, in which heat treatment causes the boundaries between grains of crystallized metal to shift. Unlike

soap film Soap films are thin layers of liquid (usually water-based) surrounded by air. For example, if two soap bubbles come into contact, they merge and a thin film is created in between. Thus, foams are composed of a network of films connected by Plate ...

s, which are forced by differences in

air pressure Atmospheric pressure, also known as barometric pressure (after the barometer), is the pressure within the atmosphere of Earth. The standard atmosphere (symbol: atm) is a unit of pressure defined as , which is equivalent to 1013.25 millibars, ...

to become surfaces of constant

mean curvature In mathematics, the mean curvature H of a surface S is an ''extrinsic'' measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space. The ...

, the grain boundaries in annealing are subject only to local effects, which cause them to move according to the mean curvature flow. The one-dimensional case of this flow, the curve-shortening flow, corresponds to annealing sheets of metal that are thin enough for the grains to become effectively two-dimensional and their boundaries to become one-dimensional.

Shape analysis

image processing An image is a visual representation of something. It can be two-dimensional, three-dimensional, or somehow otherwise feed into the visual system to convey information. An image can be an artifact, such as a photograph or other two-dimension ...

and

computer vision Computer vision is an interdisciplinary scientific field that deals with how computers can gain high-level understanding from digital images or videos. From the perspective of engineering, it seeks to understand and automate tasks that the hu ...

, suggest applying the curve-shortening flow to the outline of a shape derived from a digital image, in order to remove noise from the shape and provide a

scale space Scale-space theory is a framework for multi-scale signal representation developed by the computer vision, image processing and signal processing communities with complementary motivations from physics and biological vision. It is a formal the ...

that provides a simplified description of the shape at different levels of resolution. The method of Mokhtarian and Mackworth involves computing the curve-shortening flow, tracking the

s of the curve as they progress through the flow, and drawing a graph that plots the positions of the inflection points around the curve against the time parameter. The inflection points will typically be removed from the curve in pairs as the curve becomes convex (according to the Gage–Hamilton–Grayson theorem) and the lifetime of a pair of points corresponds to the salience of a feature of the shape. Because of the resampled convolution method that they describe for computing a numerical approximation of the curve-shortening flow, they call their method the ''resampled curvature scale space''. They observe that this scale space is invariant under Euclidean transformations of the given shape, and assert that it uniquely determines the shape and is robust against small variations in the shape. They compare it experimentally against several related alternative definitions of a scale space for shapes, and find that the resampled curvature scale space is less computationally intensive, more robust against nonuniform noise, and less strongly influenced by small-scale shape differences.

Reaction–diffusion

s modeled by the Allen–Cahn equation, the limiting behavior for fast reaction, slow diffusion, and two or more local minima of energy with the same energy level as each other is for the system to settle into regions of different local minima, with the fronts delimiting boundaries between these regions evolving according to the curve-shortening flow.

Cellular automata

In a

cellular automaton A cellular automaton (pl. cellular automata, abbrev. CA) is a discrete model of computation studied in automata theory. Cellular automata are also called cellular spaces, tessellation automata, homogeneous structures, cellular structures, tessel ...

, each cell in an infinite grid of cells may have one of a finite set of states, and all cells update their states simultaneously based only on the configuration of a small set of neighboring cells. A Life-like cellular automaton rule is one in which the grid is the infinite square lattice, there are exactly two cell states, the set of neighbors of each cell are the eight neighbors of the

Moore neighborhood In cellular automata, the Moore neighborhood is defined on a two-dimensional square lattice and is composed of a central cell and the eight cells that surround it. Name The neighborhood is named after Edward F. Moore, a pioneer of cellular a ...

, and the update rule depends only on the number of neighbors with each of the two states rather than on any more complicated function of those states. In one particular life-like rule, introduced by Gerard Vichniac and called the twisted majority rule or annealing rule, the update rule sets the new value for each cell to be the majority among the nine cells given by it and its eight neighbors, except when these cells are split among four with one state and five with the other state, in which case the new value of the cell is the minority rather than the majority. The detailed dynamics of this rule are complicated, including the existence of small stable structures. However, in the aggregate (when started with all cells in random states) it tends to form large regions of cells that are all in the same state as each other, with the boundaries between these regions evolving according to the curve-shortening flow.

Construction of closed geodesics

The curve-shortening flow can be used to prove an

for surfaces whose

Gaussian curvature In differential geometry, the Gaussian curvature or Gauss curvature of a surface at a point is the product of the principal curvatures, and , at the given point: K = \kappa_1 \kappa_2. The Gaussian radius of curvature is the reciprocal of . ...

is a non-increasing function of the distance from the

origin Origin(s) or The Origin may refer to: Arts, entertainment, and media Comics and manga * ''Origin'' (comics), a Wolverine comic book mini-series published by Marvel Comics in 2002 * ''The Origin'' (Buffy comic), a 1999 ''Buffy the Vampire Sl ...

, such as the

paraboloid In geometry, a paraboloid is a quadric surface that has exactly one axis of symmetry and no center of symmetry. The term "paraboloid" is derived from parabola, which refers to a conic section that has a similar property of symmetry. Every pla ...

. On such a surface, the smooth compact set that has any given area and minimum perimeter for that area is necessarily a circle centered at the origin. The proof applies the curve-shortening flow to two curves, a metric circle and the boundary of any other compact set, and compares the change in perimeter of the two curves as they are both reduced to a point by the flow. The curve-shortening flow can also be used to prove the

theorem of the three geodesics In differential geometry the theorem of the three geodesics, also known as Lyusternik–Schnirelmann theorem, states that every Riemannian manifold with the topology of a sphere has at least three simple closed geodesics (i.e. three embedded geo ...

, that every smooth Riemannian manifold topologically equivalent to a sphere has three geodesics that form

Related flows

Other geometric flows related to the curve-shortening flow include the following ones. * For simulating the behavior of

crystal A crystal or crystalline solid is a solid material whose constituents (such as atoms, molecules, or ions) are arranged in a highly ordered microscopic structure, forming a crystal lattice that extends in all directions. In addition, macr ...

s or other

anisotropic Anisotropy () is the property of a material which allows it to change or assume different properties in different directions, as opposed to isotropy. It can be defined as a difference, when measured along different axes, in a material's physi ...

materials, it is important to have variants of the curve-shortening flow for which the speed of flow depends on the orientation of a curve as well as on its curvature. One way of doing this is to define the energy of a curve to be the integral of a

smooth function In mathematical analysis, the smoothness of a function is a property measured by the number of continuous derivatives it has over some domain, called ''differentiability class''. At the very minimum, a function could be considered smooth if ...

of its normal vectors, and form the gradient flow of this energy, according to which the normal speed at which the curve flows is proportional to an anisotropic analog of the curvature. This flow can be simulated by discretizing the curve as a polygon. In numerical experiments, initial curves appear to converge to the Wulff shape for before shrinking to a point. Alternatively, one can let the curve flow with speed where is the (usual) curvature and and are smooth functions of the orientation . When and (so that the flow is invariant under

point reflection In geometry, a point reflection (point inversion, central inversion, or inversion through a point) is a type of isometry of Euclidean space. An object that is invariant under a point reflection is said to possess point symmetry; if it is invari ...

), the resulting flow can be shown to obey the avoidance principle and an analog of the Gage–Hamilton–Grayson theorem. * The affine curve-shortening flow was first investigated by and . In this flow, the normal speed of the curve is proportional to the cube root of the curvature. The resulting flow is invariant (with a corresponding time scaling) under the

affine transformation In Euclidean geometry, an affine transformation or affinity (from the Latin, ''affinis'', "connected with") is a geometric transformation that preserves lines and parallelism, but not necessarily Euclidean distances and angles. More generall ...

s of the Euclidean plane, a larger

symmetry group In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the ambi ...

than the similarity transformations under which the curve-shortening flow is invariant. Under this flow, an analogue of the Gage–Hamilton–Grayson theorem applies, under which any simple closed curve eventually becomes convex and then converges to an

ellipse In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in ...

as it collapses to a point.; , Theorem 3.28, p. 47. * Transforming a curve with equal normal speeds at all points has been called the grassfire transform. Curves evolved in this way will in general develop sharp corners, the trace of which forms the

medial axis The medial axis of an object is the set of all points having more than one closest point on the object's boundary. Originally referred to as the topological skeleton, it was introduced in 1967 by Harry Blum as a tool for biological shape reco ...

of the curve. A closely related curve evolution which moves straight segments of a polygonal curve at equal speeds but allows concave corners to move more quickly than unit speed instead forms a different type of

topological skeleton In shape analysis, skeleton (or topological skeleton) of a shape is a thin version of that shape that is equidistant to its boundaries. The skeleton usually emphasizes geometrical and topological properties of the shape, such as its connectivity, ...

of the given curve, its straight skeleton. * For surfaces in higher dimensions, there is more than one definition of curvature, including extrinsic (embedding-dependent) measures such as the

and intrinsic measures such as the

scalar curvature In the mathematical field of Riemannian geometry, the scalar curvature (or the Ricci scalar) is a measure of the curvature of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the geometry ...

and

Ricci curvature In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, is a geometric object which is determined by a choice of Riemannian or pseudo-Riemannian metric on a manifold. It can be considered, broadly, as a measure ...

. Correspondingly, there are several ways of defining geometric flows based on curvature, including the

(in which the normal speed of an embedded surface is its mean curvature), the

Ricci flow In the mathematical fields of differential geometry and geometric analysis, the Ricci flow ( , ), sometimes also referred to as Hamilton's Ricci flow, is a certain partial differential equation for a Riemannian metric. It is often said to be analo ...

(an intrinsic flow on the metric of a space based on its Ricci curvature), the Gauss curvature flow, and the Willmore flow (the gradient flow for an energy functional combining the mean curvature and Gaussian curvature). The curve-shortening flow is a special case of the mean curvature flow and of the Gauss curvature flow for one-dimensional curves. * In real-time path planning for mobile robots, a modified version of the curve-shortening flow with additional forces has been used to find paths that strike a balance between being short and staying clear of obstacles. * Inspired by the curve-shortening flow on smooth curves, researchers have studied methods for flowing

s so that they stay polygonal, with applications including pattern formation and synchronization in distributed systems of robots. Length-preserving polygonal flows can be used to solve the carpenter's rule problem. * In

, the

active contour model Active contour model, also called snakes, is a framework in computer vision introduced by Michael Kass, Andrew Witkin, and Demetri Terzopoulos for delineating an object outline from a possibly noisy 2D image. The snakes model is popular in comput ...

for

edge detection Edge detection includes a variety of mathematical methods that aim at identifying edges, curves in a digital image at which the image brightness changes sharply or, more formally, has discontinuities. The same problem of finding discontinuitie ...

and

image segmentation In digital image processing and computer vision, image segmentation is the process of partitioning a digital image into multiple image segments, also known as image regions or image objects ( sets of pixels). The goal of segmentation is to simpl ...

is based on curve shortening, and evolves curves based on a combination of their curvature and the features of an image.

Notes

References

* . * . * . * . * . * . * . * . * . * . * * * * . * . * . * . * . * . * . * . * . * . See in particular Example 1, pp. 542–544 and 601–604. * . * . * . * . * . * . * . * . *. * . * . * . * . * . * . * . * . * . * . * . * . * . * . * . * . * . * . * . * . * . * . * . * . * * . * . * . Also published in . * . * . * . * . * . Reprinted in . * . * . * . * . * . * . * . * . * . * . * . * . {{refend Geometric flow