Two-state Quantum System

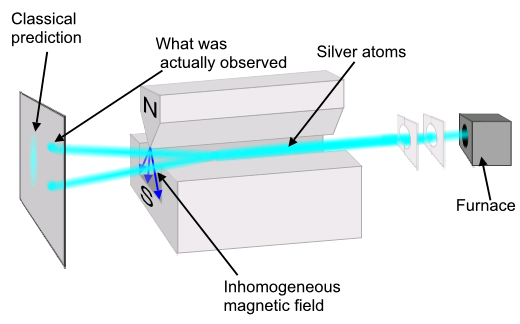In quantum mechanics, a two-state system (also known as a two-level system) is a quantum system that can exist in any quantum superposition of two independent (physically distinguishable) quantum states. The Hilbert space describing such a system is two-dimensional. Therefore, a complete basis spanning the space will consist of two independent states. Any two-state system can also be seen as a qubit.

Two-state systems are the simplest quantum systems that are of interest, since the dynamics of a one-state system is trivial (as there are no other states the system can exist in). The mathematical framework required for the analysis of two-state systems is that of linear differential equations and linear algebra of two-dimensional spaces. As a result, the dynamics of a two-state system can be solved analytically without any approximation. The generic behavior of the system is that the wavefunction's amplitude oscillates between the two states.

A very well known example of a two-state system is the spin of a spin-1/2 particle such as an electron, whose spin can have values +''ħ''/2 or −''ħ''/2, where ''ħ'' is the reduced Planck constant.

The two-state system cannot be used as a description of absorption or decay, because such processes require coupling to a continuum. Such processes would involve exponential decay of the amplitudes, but the solutions of the two-state system are oscillatory.

Analytical solutions for stationary state energies and time-dependence

Representation

Supposing the two available basis states of the system are $, 1\rangle$ and $, 2\rangle$, in general the state can be written as a superposition of these two states with probability amplitudes $c_1, c_2$,
$, \psi\rangle = c_1 , 1\rangle + c_2 , 2\rangle .$

Since the basis states are orthonormal, $\langle i, j\rangle=\delta_$ where $i,j\in$ and $\delta_$ is the Kronecker delta, so $c_i=\langle i, \psi\rangle$. These two complex numbers may be considered coordinates in a two-dimensional complex Hilbert space. Thus the state vector corresponding to the state $, \psi\rangle$ is
$, \psi\rangle \equiv \begin \langle 1, \psi\rangle \\ \langle 2, \psi\rangle\end=\begin c_1 \\ c_2\end=c_1\begin 1 \\ 0\end + c_2\begin 0 \\ 1\end=\mathbf,$
and the basis states correspond to the basis vectors, $, 1\rangle \equiv \begin \langle 1, 1\rangle \\ \langle 2, 1\rangle\end = \begin 1 \\ 0\end$ and $, 2\rangle \equiv \begin \langle 1, 2\rangle \\ \langle 2, 2\rangle\end = \begin 0 \\ 1\end.$

If the state $, \psi\rangle$ is normalized, the norm of the state vector is unity, i.e. $^2+^2 = 1$.

All observable physical quantities, such as energy, are associated with hermitian operators. In the case of energy and the corresponding Hamiltonian, , this means
$H_=\langle i, H, j \rangle=\langle j, H, i \rangle^*=H_^*,$
i.e. $H_$ and $H_$ are real, and $H_ = H_^*$. Thus, these four matrix elements $H_$ produce a 2×2 hermitian matrix,
$\mathbf = \begin \langle 1, H, 1 \rangle & \langle 1, H, 2 \rangle \\ \langle 2, H, 1 \rangle & \langle 2, H, 2 \rangle \end = \begin H_ & H_ \\ H_^* & H_ \end .$

The time-independent Schrödinger equation states that $H, \psi\rangle=E, \psi\rangle$; substituting for $, \psi\rangle$ in terms of the basis states from above, and multiplying both sides by $\langle 1,$ or $\langle 2,$ produces a system of two linear equations that can be written in matrix form,
$\begin H_ & H_ \\ H_^* & H_ \end \begin c_1 \\ c_2 \end = E \begin c_1 \\ c_2 \end ,$
or $\mathbf = E\mathbf$ which is a 2×2 matrix eigenvalues and eigenvectors problem. As mentioned above, this equation comes from plugging a general state into the time-independent Schrödinger equation. Remember that the time-independent Schrödinger equation is a restrictive condition used to specify the eigenstates. Therefore, when plugging a general state into it, we are seeing what form the general state must take to be an eigenstate. Doing so, and distributing, we get $c_1 H , 1 \rangle + c_2 H , 2 \rangle = c_1 E , 1 \rangle + c_2 E , 2 \rangle$, which requires $c_1$ or $c_2$ to be zero ($E$ cannot be equal to both $\varepsilon_1$ and $\varepsilon_2$, the energies of the individual states, which are by definition different). Upon setting $c_1$ or $c_2$ to be 0, only one state remains, and $E$ is the energy of the surviving state. This result is a redundant reminder that the time-independent Schrödinger equation is only satisfied by eigenstates of H, which are (by definition of the state vector) the states where all except one coefficient are zero. Now, if we follow the same derivation, but before acting with the Hamiltonian on the individual states, we multiply both sides by $\langle 1 ,$ or $\langle 2 ,$, we get a system of two linear equations that can be combined into the above matrix equation. Like before, this can only be satisfied if $c_1$ or $c_2$ is zero, and when this happens, the constant $E$ will be the energy of the remaining state. The above matrix equation should thus be interpreted as a restrictive condition on a general state vector to yield an eigenvector of $H$, exactly analogous to the time-independent Schrödinger equation.

Of course, in general, commuting the matrix with a state vector will not result in the same vector multiplied by a constant ''E.'' For general validity, one has to write the equation in the form
$\begin H_ & H_ \\ H_^* & H_ \end \begin c_1 \\ c_2 \end = \begin \varepsilon_1 c_1 \\ \varepsilon_2 c_2 \end ,$
with the individual eigenstate energies still inside the product vector. In either case, the Hamiltonian matrix can be derived using the method specified above, or via the more traditional method of constructing a matrix using boundary conditions; specifically, by using the requirement that when it acts on either basis state, it must return that state multiplied by the energy of that state. (There are no boundary conditions on how it acts on a general state.) This results in a diagonal matrix with the diagonal elements being the energies of the eigenstates and the off-diagonal elements being zero. The form of the matrix above that uses bra-ket-enclosed Hamiltonians is a more generalized version of this matrix.

One might ask why it is necessary to write the Hamiltonian matrix in such a general form with bra-ket-enclosed Hamiltonians, since $H_, i\neq j$ should always equal zero and $H_$ should always equal $\varepsilon_i$. The reason is that, in some more complex problems, the state vectors may not be eigenstates of the Hamiltonian used in the matrix. One place where this occurs is in degenerate perturbation theory, where the off-diagonal elements are nonzero until the problem is solved by diagonalization.

Because of the hermiticity of $\mathbf$ the eigenvalues are real; or, rather, conversely, it is the requirement that the energies are real that implies the hermiticity of $\mathbf$. The eigenvectors represent the stationary states, i.e., those for whom the absolute magnitude of the squares of the probability amplitudes do not change with time.

Eigenvalues of the Hamiltonian

The most general form of a 2×2 Hermitian matrix such as the Hamiltonian of a two-state system is given by
$\mathbf = \begin \varepsilon_1 & \beta - i \gamma \\ \beta + i\gamma & \varepsilon_2\end,$
where $\varepsilon_1, \varepsilon_2, \beta$ and are real numbers with units of energy. The allowed energy levels of the system, namely the eigenvalues of the Hamiltonian matrix, can be found in the usual way.

Equivalently, this matrix can be decomposed as,
$\mathbf = \alpha\cdot\sigma_0 + \beta \cdot\sigma_1 + \gamma\cdot\sigma_2 + \delta\cdot\sigma_3 = \begin \alpha+\delta & \beta-i\gamma\\ \beta+i\gamma & \alpha-\delta \end.$
Here, $\alpha = \frac 1 2 \left(\varepsilon_1 + \varepsilon_2\right)$ and $\delta = \frac 1 2 \left(\varepsilon_1 - \varepsilon_2\right)$ are real numbers. The matrix $\sigma_0$ is the 2×2 identity matrix and the matrices $\sigma_k$ with $k = 1,2,3$ are the Pauli matrices. This decomposition simplifies the analysis of the system, especially in the time-independent case, where the values of $\alpha,\beta,\gamma$ and $\delta$ are constants.

The Hamiltonian can be further condensed as
$\mathbf = \alpha \cdot \sigma_0 + \mathbf\cdot \boldsymbol .$

The vector $\mathbf$ is given by $(\beta,\gamma,\delta)$ and $\sigma$ is given by $(\sigma_1,\sigma_2,\sigma_3)$. This representation simplifies the analysis of the time evolution of the system and is easier to use with other specialized representations such as the Bloch sphere.

If the two-state system's time-independent Hamiltonian is defined as above, then its eigenvalues are given by $E_ = \alpha \pm , \mathbf,$. Evidently, ''α'' is the average energy of the two levels, and the norm of $\mathbf$ is the splitting between them. The corresponding eigenvectors are denoted as $, +\rangle$ and $, -\rangle$.

Time dependence

We now assume that the probability amplitudes are time-dependent, though the basis states are not. The Time-dependent Schrödinger equation states $i\hbar \partial_t , \psi\rangle = H, \psi\rangle$, and proceeding as before (substituting for $, \psi\rangle$ and premultiplying by $\langle 1, , \langle 2,$ again produces a pair of coupled linear equations, but this time they are first order partial differential equations: $i\hbar \partial_t \mathbf = \mathbf$. If $\mathbf$ is time independent there are several approaches to find the time dependence of $c_1, c_2$, such as normal modes. The result is that
$\mathbf(t) = e^ \mathbf_0 = \mathbf(t) \mathbf_0.$
where $\mathbf_0 = \mathbf(0)$ is the statevector at $t = 0$.
Here the exponential of a matrix may be found from the series expansion. The matrix $\mathbf(t)$ is called the time evolution matrix (which comprises the matrix elements of the corresponding time evolution operator $U(t)$). It is easily proved that $\mathbf(t)$ is unitary, meaning that $\mathbf^\dagger \mathbf = 1$.

It can be shown that
$\mathbf(t) = e^ = e^ \left(\cos\left(\fract\right)\sigma_0 - i \sin\left(\fract\right) \hat \cdot \boldsymbol\right) ,$
where $\hat = \frac.$

When one changes the basis to the eigenvectors of the Hamiltonian, in other words, if the basis states $, 1\rangle , , 2\rangle$ are chosen to be the eigenvectors, then $\epsilon_1=H_=\langle 1, H, 1 \rangle=E_1\langle 1, 1 \rangle=E_1$ and $\beta+i\gamma = H_ =\langle 2, H, 1 \rangle = E_1\langle 2, 1 \rangle = 0$ and so the Hamiltonian is diagonal, i.e. $, \mathbf, = \delta$ and is of the form,
$\mathbf = \begin E_1 & 0 \\ 0 & E_2 \end.$

Now, the unitary time evolution operator $U$ is easily seen to be given by:
$\mathbf(t) = e^ = \begin e^ & 0\\ 0 & e^ \end = e^ \begin e^ & 0\\ 0 & e^ \end = e^ \left(\cos\left(\frac \delta \hbar t\right)\sigma_0 - i \sin\left(\frac \delta \hbar t\right) \boldsymbol_3\right) .$
The $e^$ factor merely contributes to the overall phase of the operator, and can usually be ignored to yield a new time evolution operator that is physically indistinguishable from the original operator. Moreover, any perturbation to the system (which will be of the same form as the Hamiltonian) can be added to the system in the eigenbasis of the unperturbed Hamiltonian and analysed in the same way as above. Therefore, for any perturbation the new eigenvectors of the perturbed system can be solved for exactly, as mentioned in the introduction.

Rabi formula for a static perturbation

Suppose that the system starts in one of the basis states at $t = 0$, say $, 1\rangle$ so that $\mathbf_0 = \begin 1\\ 0 \end$, and we are interested in the probability of occupation of each of the basis states as a function of time when $\mathbf$ is the time-independent Hamiltonian.
$\mathbf(t) =\mathbf(t)\mathbf_0= \begin U_(t) & U_(t)\\ U_(t) & U_(t) \end\begin 1\\ 0 \end=\begin U_(t) \\ U_(t) \end.$

The probability of occupation of state is $P_i(t) = , c_i(t), ^2 = , U_(t), ^2$. In the case of the starting state, $P_1(t) = , c_1(t), ^2 = , U_(t), ^2$, and from above, $U_(t) = e^ \left(\cos\left(\frac\hbar t\right) - i \sin\left(\frac\hbar t\right)\frac\right) .$ Hence,
$P_1(t)= \cos^2(\Omega t) + \sin^2(\Omega t)\frac.$

Obviously, $P_1(0)=1$ due to the initial condition. The frequency $\Omega = \frac = \frac 1 \hbar \sqrt = \sqrt$ is called the generalised Rabi frequency, $\Omega_R = (\beta+i \gamma)/\hbar$ is called the Rabi frequency, and $\Delta = \delta/\hbar$ is called the detuning.

At zero detuning, $P_1(t) = \cos^2(, \Omega_R, t)$, i.e., there is Rabi flopping from guaranteed occupation of state 1, to guaranteed occupation of state 2, and back to state 1, etc., with frequency $, \Omega_R,$. As the detuning is increased away from zero, the frequency of the flopping increases (to ) and the amplitude of exciting the electron decreases to $\Omega^2/\Delta^2$.

For time dependent Hamiltonians induced by light waves, see the articles on ''Rabi cycle'' and ''rotating wave approximation''.

Some important two-state systems

Precession in a field

Consider the case of a spin-1/2 particle in a magnetic field $\mathbf = B\mathbf$. The interaction Hamiltonian for this system is

:$H=-\boldsymbol\cdot\mathbf=-\mu\boldsymbol\cdot\mathbf,$

where $\mu$ is the magnitude of the particle's magnetic moment and $\boldsymbol$ is the vector of Pauli matrices. Solving the time dependent Schrödinger equation $H\psi = i\hbar \partial_t \psi$ yields

:$\psi(t) = e^ \psi(0),$

where $\omega = \mu B/\hbar$ and $e^ = \cos I + i\; \mathbf\cdot\boldsymbol \sin$. Physically, this corresponds to the Bloch vector precessing around $\mathbf$ with angular frequency $2\omega$. Without loss of generality, assume the field is uniform points in $\mathbf$, so that the time evolution operator is given as

:$e^ = \begin e^ & 0 \\ 0 & e^ \end.$

It can be seen that such a time evolution operator acting on a general spin state of a spin-1/2 particle will lead to the precession about the axis defined by the applied magnetic field (this is the quantum mechanical equivalent of Larmor precession)

The above method can be applied to the analysis of any generic two-state system that is interacting with some field (equivalent to the magnetic field in the previous case) if the interaction is given by an appropriate coupling term that is analogous to the magnetic moment. The precession of the state vector (which need not be a physical spinning as in the previous case) can be viewed as the precession of the state vector on the Bloch sphere.

The representation on the Bloch sphere for a state vector $\psi(0)$ will simply be the vector of expectation values $\mathbf=\left(\langle \sigma_x \rangle,\langle \sigma_y \rangle,\langle \sigma_z \rangle \right)$. As an example, consider a state vector $\psi(0)$ that is a normalized superposition of $\left, \uparrow\right\rangle$ and $\left, \downarrow\right\rangle$, that is, a vector that can be represented in the $\sigma_z$ basis as

:$\psi(0) = \frac\begin 1 \\ 1 \end$

The components of $\psi(t)$ on the Bloch sphere will simply be $\mathbf=\left(\cos,-\sin,0\right)$. This is a unit vector that begins pointing along $\mathbf$ and precesses around $\mathbf$ in a left-handed manner. In general, by a rotation around $\mathbf$, any state vector $\psi(0)$ can be represented as $a\left, \uparrow\right\rangle + b\left, \downarrow\right\rangle$ with real coefficients $a$ and $b$. Such a state vector corresponds to a Bloch vector in the ''xz''-plane making an angle $\tan(\theta/2) = b/a$ with the ''z''-axis. This vector will proceed to precess around $\mathbf$. In theory, by allowing the system to interact with the field of a particular direction and strength for precise durations, it is possible to obtain any orientation of the Bloch vector, which is equivalent to obtaining any complex superposition. This is the basis for numerous technologies including quantum computing and MRI.

Evolution in a time-dependent field: Nuclear magnetic resonance

Nuclear magnetic resonance (NMR) is an important example in the dynamics of two-state systems because it is involves the exact solution to a time dependent Hamiltonian. The NMR phenomenon is achieved by placing a nucleus in a strong, static field B₀ (the "holding field") and then applying a weak, transverse field B₁ that oscillates at some radiofrequency ''ω''_r.Griffiths, p. 377. Explicitly, consider a spin-1/2 particle in a holding field $B_0 \mathbf$ and a transverse rf field B₁ rotating in the ''xy''-plane in a right-handed fashion around B₀:

:$\mathbf = \begin B_1 \cos\omega_\mathrm t \\ B_1 \sin\omega_\mathrm t\\ B_0 \end.$

As in the free precession case, the Hamiltonian is $H = -\mu\boldsymbol\cdot\mathbf$, and the evolution of a state vector $\psi(t)$ is found by solving the time-dependent Schrödinger equation $H\psi = i\hbar\,\partial \psi/\partial t$. After some manipulation (given in the collapsed section below), it can be shown that the Schrödinger equation becomes

:$\frac=i\left(\omega_1 \sigma_x + \left(w_0+\frac\right)\sigma_z\right)\psi,$
where $\omega_0 = \mu B_0/\hbar$ and $\omega_1 = \mu B_1/\hbar$.

As per the previous section, the solution to this equation has the Bloch vector precessing around $(\omega_1,0,\omega_0 + \omega_r/2)$ with a frequency that is twice the magnitude of the vector. If $\omega_0$ is sufficiently strong, some proportion of the spins will be pointing directly down prior to the introduction of the rotating field. If the angular frequency of the rotating magnetic field is chosen such that $\omega_r = -2 \omega_0$, in the rotating frame the state vector will precess around $\hat$ with frequency $2 \omega_1$, and will thus flip from down to up releasing energy in the form of detectable photons. This is the fundamental basis for NMR, and in practice is accomplished by scanning $\omega_r$ until the resonant frequency is found at which point the sample will emit light. Similar calculations are done in atomic physics, and in the case that the field is not rotating, but oscillating with a complex amplitude, use is made of the rotating wave approximation in deriving such results.

Relation to Bloch equations

The optical Bloch equations for a collection of spin-1/2 particles can be derived from the time dependent Schrödinger equation for a two level system. Starting with the previously stated Hamiltonian $i\hbar\partial_t\psi=-\mu\vec\cdot\vec\psi$, it can be written in summation notation after some rearrangement as

:$\frac=i\frac\sigma_i B_i \psi$

Multiplying by a Pauli matrix $\sigma_i$ and the conjugate transpose of the wavefunction, and subsequently expanding the product of two Pauli matrices yields

:$\psi^\dagger \sigma_j \frac=i\frac\psi^\dagger\sigma_j\sigma_i B_i \psi =i\frac\psi^\dagger \left(I\delta_ - i \sigma_k \varepsilon_\right)B_i\psi=\frac\psi^\dagger \left(iI\delta_ + \sigma_k \varepsilon_\right)B_i\psi$

Adding this equation to its own conjugate transpose yields a left hand side of the form

:$\psi^\dagger \sigma_j \frac + \frac \sigma_j \psi = \frac$

And a right hand side of the form

:$\frac\psi^\dagger \left(iI\delta_ + \sigma_k \varepsilon_\right)B_i\psi + \frac\psi^\dagger \left(-iI\delta_ + \sigma_k \varepsilon_\right)B_i\psi = \frac \left( \psi^\dagger\sigma_k\psi\right) B_i \varepsilon_$

As previously mentioned, the expectation value of each Pauli matrix is a component of the Bloch vector, $\langle \sigma_i \rangle = \psi^\dagger\sigma_i\psi = R_i$. Equating the left and right hand sides, and noting that $\frac$ is the gyromagnetic ratio $\gamma$, yields another form for the equations of motion of the Bloch vector

:$\frac = \gamma R_k B_i \varepsilon_$

where the fact that $\varepsilon_ = \varepsilon_$ has been used. In vector form these three equations can be expressed in terms of a cross product

:$\frac = \gamma \vec \times \vec$
Classically, this equation describes the dynamics of a spin in a magnetic field. An ideal magnet consists of a collection of identical spins behaving independently, and thus the total magnetization $\vec$ is proportional to the Bloch vector $\vec$. All that is left to obtain the final form of the optical Bloch equations is the inclusion of the phenomenological relaxation terms.

As a final aside, the above equation can be derived by considering the time evolution of the angular momentum operator in the Heisenberg picture.

: i\hbar\frac= sigma_j,H sigma_j, -\mu \sigma_i B_i-\mu\left(\sigma_j\sigma_i B_i - \sigma_i\sigma_j B_i\right)=\mu sigma_i,\sigma_j_i = 2\mu i \varepsilon_\sigma_k B_i

When coupled with the fact that $\vec = \langle \sigma_i \rangle$, this equation is the same equation as before.

Validity

Two-state systems are the simplest non-trivial quantum systems that occur in nature, but the above-mentioned methods of analysis are not just valid for simple two-state systems. Any general multi-state quantum system can be treated as a two-state system as long as the observable one is interested in has two eigenvalues. For example, a spin-1/2 particle may in reality have additional translational or even rotational degrees of freedom, but those degrees of freedom are irrelevant to the preceding analysis. Mathematically, the neglected degrees of freedom correspond to the degeneracy of the spin eigenvalues.

Another case where the effective two-state formalism is valid is when the system under consideration has two levels that are effectively decoupled from the system. This is the case in the analysis of the spontaneous or stimulated emission of light by atoms and that of charge qubits. In this case it should be kept in mind that the perturbations (interactions with an external field) are in the right range and do not cause transitions to states other than the ones of interest.

Significance and other examples

Pedagogically, the two-state formalism is among the simplest of mathematical techniques used for the analysis of quantum systems. It can be used to illustrate fundamental quantum mechanical phenomena such as the interference exhibited by particles of the polarization states of the photon, but also more complex phenomena such as neutrino oscillation or the neutral K-meson oscillation.

Two-state formalism can be used to describe simple mixing of states, which leads to phenomena such as resonance stabilization and other level crossing related symmetries. Such phenomena have a wide variety of application in chemistry. Phenomena with tremendous industrial applications such as the maser and laser can be explained using the two-state formalism.

The two-state formalism also forms the basis of quantum computing. Qubits, which are the building blocks of a quantum computer, are nothing but two-state systems. Any quantum computational operation is a unitary operation that rotates the state vector on the Bloch sphere.

Further reading

* An excellent treatment of the two-state formalism and its application to almost all the applications mentioned in this article is presented in the third volume of ''The Feynman Lectures on Physics''.
* The following set of lecture notes covers the necessary mathematics and also treats a few examples in some detail:
** from the ''Quantum mechanics II'' course offered at MIT, http://web.mit.edu/8.05/handouts/Twostates_03.pdf
** from the same course dealing with neutral particle oscillation, http://web.mit.edu/8.05/handouts/nukaon_07.pdf
** from the ''Quantum mechanics I'' course offered at TIFR, http://theory.tifr.res.in/~sgupta/courses/qm2013/hand4.pdf covers the essential mathematics
** http://theory.tifr.res.in/~sgupta/courses/qm2013/hand5.pdf ; from the same course deals with the some physical two-state systems and other important aspects of the formalism
** the mathematical in the initial section is done in a manner similar to these notes http://www.math.columbia.edu/~woit/QM/qubit.pdf, which are from the ''Quantum Mechanics for Mathematicians'' course offered at University of Columbia.
** a book version of the same ; http://www.math.columbia.edu/~woit/QM/qmbook.pdf
** Two-state systems and the two-sphere, R J Plymen, Il Nuovo Cimento B 13 (1973) 55-58

See also

* Rabi cycle
* Doublet
* Nuclear magnetic resonance
* Quantum optics

References

{{DEFAULTSORT:Two-State Quantum System
Quantum models