Theodorus of Cyrene

Theodorus of Cyrene (; 450 BC) was an ancient Greek mathematician. The only first-hand accounts of him that survive are in three of Plato's dialogues: the '' Theaetetus'', the ''Sophist'', and the ''Statesman''. In the first dialogue, he posits a mathematical construction now known as the Spiral of Theodorus.

Life

Little is known as Theodorus' biography beyond what can be inferred from Plato's dialogues. He was born in the northern African colony of Cyrene, and apparently taught both there and in Athens. He complains of old age in the ''Theaetetus'', the dramatic date of 399 BC of which suggests his period of flourishing to have occurred in the mid-5th century. The text also associates him with the sophist Protagoras, with whom he claims to have studied before turning to geometry. A dubious tradition repeated among ancient biographers like Diogenes Laërtius held that Plato later studied with him in Cyrene, Libya.
This eminent mathematician Theodorus was, along with Alcibiades and many other of Socrates' companions (many of whom would be associated with the Thirty Tyrants), accused of distributing the mysteries at a symposium, according to Plutarch, who himself was priest of the temple at Delphi.

Work in mathematics

Theodorus' work is known through a sole theorem, which is delivered in the literary context of the ''Theaetetus'' and has been argued alternately to be historically accurate or fictional. In the text, his student Theaetetus attributes to him the theorem that the square roots of the non-square numbers up to 17 are irrational:

The square containing ''two'' square units is not mentioned, perhaps because the incommensurability of its side with the unit was already known.) Theodorus's method of proof is not known. It is not even known whether, in the quoted passage, "up to" (μέχρι) means that seventeen is included. If seventeen is excluded, then Theodorus's proof may have relied merely on considering whether numbers are even or odd. Indeed, Hardy and Wright
and Knorr suggest proofs that rely ultimately on the following theorem: If $x^2=ny^2$ is soluble in integers, and $n$ is odd, then $n$ must be congruent to 1 ''modulo'' 8 (since $x$ and $y$ can be assumed odd, so their squares are congruent to 1 ''modulo'' 8.

That one cannot prove the irrationality the square root of 17 by considerations restricted to the arithmetic of the even and the odd has been shown in one system of the arithmetic of the even and the odd in . and,. but it is an open problem in a stronger natural axiom system for the arithmetic of the even and the odd .

A possibility suggested earlier by Zeuthen is that Theodorus applied the so-called Euclidean algorithm, formulated in Proposition X.2 of the ''Elements'' as a test for incommensurability. In modern terms, the theorem is that a real number with an ''infinite'' continued fraction expansion is irrational. Irrational square roots have periodic expansions. The period of the square root of 19 has length 6, which is greater than the period of the square root of any smaller number. The period of √17 has length one (so does √18; but the irrationality of √18 follows from that of √2).

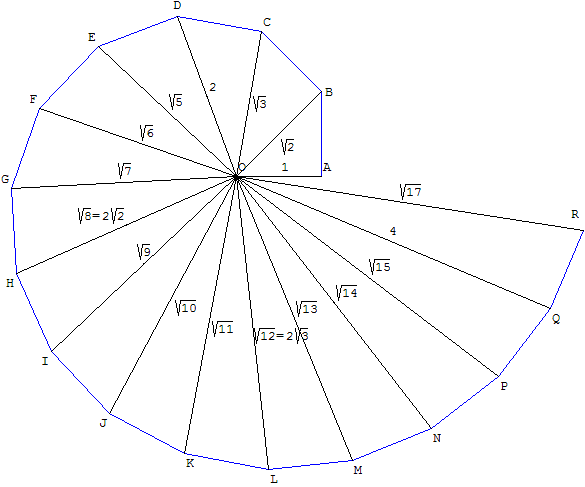
The so-called Spiral of Theodorus is composed of contiguous right triangles with hypotenuse lengths equal √2, √3, √4, …, √17; additional triangles cause the diagram to overlap. Philip J. Davis interpolated the vertices of the spiral to get a continuous curve. He discusses the history of attempts to determine Theodorus' method in his book ''Spirals: From Theodorus to Chaos'', and makes brief references to the matter in his fictional ''Thomas Gray'' series.

That Theaetetus established a more general theory of irrationals, whereby square roots of non-square numbers are irrational, is suggested in the eponymous Platonic dialogue as well as commentary on, and scholia to, the ''Elements''.

See also

* Chronology of ancient Greek mathematicians
*List of speakers in Plato's dialogues
*Quadratic irrational
* Wilbur Knorr

References

Further reading

*
*

{{DEFAULTSORT:Theodorus Of Cyrene
Ancient Greek geometers
Cyrenean Greeks
5th-century BC Greek mathematicians