HPP Model on:
[Wikipedia]
[Google]
[Amazon]
The Hardy–Pomeau–Pazzis (HPP) model is a fundamental lattice gas automaton for the simulation of gases and liquids. It was a precursor to the
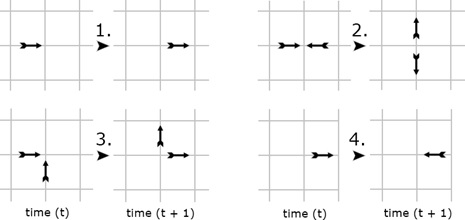 In this model, the lattice takes the form of a two-dimensional square grid, with particles capable of moving to any of the four adjacent grid points which share a common edge, and particles cannot move diagonally. This means each grid point can only have one of sixteen possible interactions.
* Particles exist only on the grid points, never on the edges or surface of the lattice.
* Each particle has an associated direction (from one grid point to another immediately adjacent grid point).
* Each lattice grid cell can only contain a maximum of one particle for each direction, i.e., contain a total of between zero and four particles.
The following rules also govern the model:
# A single particle moves in a fixed direction until it experiences a collision.
# Two particles experiencing a head-on collision are deflected perpendicularly.
# Two particles experience a collision which isn't head-on simply pass through each other and continue in the same direction.
# Optionally, when a particles collides with the edges of a lattice it can rebound.
The HPP models follows a two-stage update process.
In this model, the lattice takes the form of a two-dimensional square grid, with particles capable of moving to any of the four adjacent grid points which share a common edge, and particles cannot move diagonally. This means each grid point can only have one of sixteen possible interactions.
* Particles exist only on the grid points, never on the edges or surface of the lattice.
* Each particle has an associated direction (from one grid point to another immediately adjacent grid point).
* Each lattice grid cell can only contain a maximum of one particle for each direction, i.e., contain a total of between zero and four particles.
The following rules also govern the model:
# A single particle moves in a fixed direction until it experiences a collision.
# Two particles experiencing a head-on collision are deflected perpendicularly.
# Two particles experience a collision which isn't head-on simply pass through each other and continue in the same direction.
# Optionally, when a particles collides with the edges of a lattice it can rebound.
The HPP models follows a two-stage update process.
lattice Boltzmann methods
The lattice Boltzmann methods (LBM), originated from the lattice gas automata (LGA) method (Hardy- Pomeau-Pazzis and Frisch- Hasslacher- Pomeau models), is a class of computational fluid dynamics (CFD) methods for fluid simulation. Instead of solvi ...
. From lattice gas automata, it is possible to derive the macroscopic Navier-Stokes equations. Interest in lattice gas automaton methods levelled off in the early 1990s, due to rising interest in the lattice Boltzmann methods.
It was first introduced in papers published in 1973 and 1976 by Jean Hardy, Yves Pomeau
Yves Pomeau, born in 1942, is a French mathematician and physicist, emeritus research director at the CNRS and corresponding member of the French Academy of sciences. He was one of the founders of thLaboratoire de Physique Statistique, École No ...
and Olivier de Pazzis, whose initials give the model its name. The model can be used as a simple model for both the movement of gases and fluid.
Model
 In this model, the lattice takes the form of a two-dimensional square grid, with particles capable of moving to any of the four adjacent grid points which share a common edge, and particles cannot move diagonally. This means each grid point can only have one of sixteen possible interactions.
* Particles exist only on the grid points, never on the edges or surface of the lattice.
* Each particle has an associated direction (from one grid point to another immediately adjacent grid point).
* Each lattice grid cell can only contain a maximum of one particle for each direction, i.e., contain a total of between zero and four particles.
The following rules also govern the model:
# A single particle moves in a fixed direction until it experiences a collision.
# Two particles experiencing a head-on collision are deflected perpendicularly.
# Two particles experience a collision which isn't head-on simply pass through each other and continue in the same direction.
# Optionally, when a particles collides with the edges of a lattice it can rebound.
The HPP models follows a two-stage update process.
In this model, the lattice takes the form of a two-dimensional square grid, with particles capable of moving to any of the four adjacent grid points which share a common edge, and particles cannot move diagonally. This means each grid point can only have one of sixteen possible interactions.
* Particles exist only on the grid points, never on the edges or surface of the lattice.
* Each particle has an associated direction (from one grid point to another immediately adjacent grid point).
* Each lattice grid cell can only contain a maximum of one particle for each direction, i.e., contain a total of between zero and four particles.
The following rules also govern the model:
# A single particle moves in a fixed direction until it experiences a collision.
# Two particles experiencing a head-on collision are deflected perpendicularly.
# Two particles experience a collision which isn't head-on simply pass through each other and continue in the same direction.
# Optionally, when a particles collides with the edges of a lattice it can rebound.
The HPP models follows a two-stage update process.
Collision step
In this step, the above rules 2., 3., and 4. are checked and applied if any collisions have occurred. This results in head-on collision particles changing direction, pass-through collisions continuing unchanged, or non-colliding particles simple remaining the same.Transport step
The second step consists of each particle moving one lattice step in the direction they are currently travelling, which could have been changed by the above Collision Step.Shortcomings
The model is badly flawed, as momentum is always conserved in both the horizontal and vertical lanes. No energy is ever removed from the model, either by collisions or movement, so it will continue indefinitely. The HPP model lackedrotational invariance In mathematics, a function defined on an inner product space is said to have rotational invariance if its value does not change when arbitrary rotations are applied to its argument.
Mathematics
Functions
For example, the function
:f(x,y) = ...
, which made the model highly anisotropic
Anisotropy () is the property of a material which allows it to change or assume different properties in different directions, as opposed to isotropy. It can be defined as a difference, when measured along different axes, in a material's phys ...
. This means for example, that the vortices produced by the HPP model are square-shaped.Succi, footnote p. 22
Notes
References
* (Chapter 2 on Lattice gas Cellular Automata) *{{cite book, author=Neil Gershenfeld, title=The Nature of Mathematical Modeling, publisher=Cambridge University Press, year=1998, isbn=978-0521570954 Computational fluid dynamics