Complex quadratic polynomial on:
[Wikipedia]
[Google]
[Amazon]
 See also :
* Boettcher map which maps exterior of Mandelbrot set to the exterior of unit disc
* multiplier map which maps interior of hyperbolic component of Mandelbrot set to the interior of unit disc
See also :
* Boettcher map which maps exterior of Mandelbrot set to the exterior of unit disc
* multiplier map which maps interior of hyperbolic component of Mandelbrot set to the interior of unit disc
The Schwarzian Derivative & the Critical Orbit by Wes McKinney 18.091 20 April 2005
/ref> :
Quadratic maps as dynamical systems on the p-adic numbers
Wolf Jung : Homeomorphisms on Edges of the Mandelbrot Set. Ph.D. thesis of 2002
*More about Quadratic Maps : https://mathworld.wolfram.com/QuadraticMap.html {{DEFAULTSORT:Complex Quadratic Polynomial Complex dynamics Fractals Polynomials
A complex quadratic polynomial is a
Paritition of dynamic plane of quadratic polynomial for 1 4.svg, 1/4
Paritition of dynamic plane of quadratic polynomial for 1 6.svg, 1/6
Paritition of dynamic plane of quadratic polynomial for 9 56.svg, 9/56
Paritition of dynamic plane of quadratic polynomial for 129 over 16256.svg, 129/16256
Julia set for z^2+0.7i*z.png, attracting
IntLSM_J.jpg, attracting
ILSMJ.png, attracting
Level sets of attraction time to parabolic fixed point in the fat basilica Julia set.png, parabolic
Quadratic Julia set with Internal level sets for internal ray 0.ogv, Video for c along internal ray 0



 The forward orbit of a critical point is called a critical orbit. Critical orbits are very important because every attracting
The forward orbit of a critical point is called a critical orbit. Critical orbits are very important because every attracting
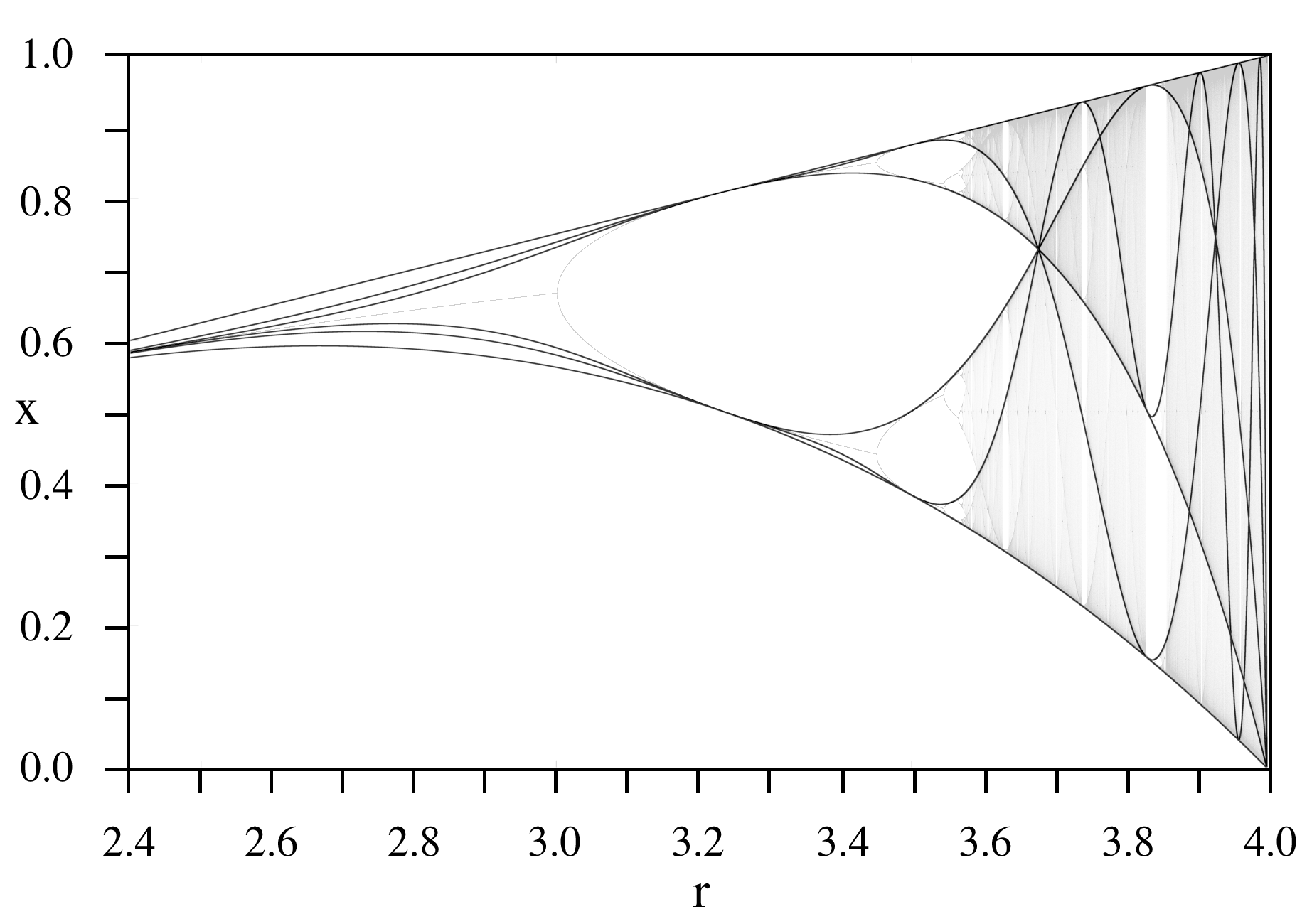 Diagrams of critical polynomials are called critical curves.
These curves create the skeleton (the dark lines) of a
Diagrams of critical polynomials are called critical curves.
These curves create the skeleton (the dark lines) of a
 In this space there are two basic types of 2D planes:
* the dynamical (dynamic) plane, -plane or ''c''-plane
* the parameter plane or ''z''-plane
There is also another plane used to analyze such dynamical systems ''w''-plane:
* the conjugation plane
* model plane
In this space there are two basic types of 2D planes:
* the dynamical (dynamic) plane, -plane or ''c''-plane
* the parameter plane or ''z''-plane
There is also another plane used to analyze such dynamical systems ''w''-plane:
* the conjugation plane
* model plane
phase space
In dynamical system theory, a phase space is a space in which all possible states of a system are represented, with each possible state corresponding to one unique point in the phase space. For mechanical systems, the phase space usuall ...
of a quadratic map is called its parameter plane. Here:
is constant and is variable.
There is no dynamics here. It is only a set of parameter values. There are no orbits on the parameter plane.
The parameter plane consists of:
* The quadratic polynomial
In mathematics, a quadratic polynomial is a polynomial of degree two in one or more variables. A quadratic function is the polynomial function defined by a quadratic polynomial. Before 20th century, the distinction was unclear between a polynomial ...
whose coefficient
In mathematics, a coefficient is a multiplicative factor in some term of a polynomial, a series, or an expression; it is usually a number, but may be any expression (including variables such as , and ). When the coefficients are themselves ...
s and variable are complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the fo ...
s.
Properties
Quadratic polynomials have the following properties, regardless of the form: *It is a unicritical polynomial, i.e. it has one finite critical point in the complex plane, Dynamical plane consist of maximally 2 basins: basin of infinity and basin of finite critical point ( if finite critical point do not escapes) *It can be postcritically finite, i.e. the orbit of the critical point can be finite, because the critical point is periodic or preperiodic. * It is a unimodal function, * It is arational function
In mathematics, a rational function is any function that can be defined by a rational fraction, which is an algebraic fraction such that both the numerator and the denominator are polynomials. The coefficients of the polynomials need not be ...
,
* It is an entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic on the whole complex plane. Typical examples of entire functions are polynomials and the exponential function, and any fin ...
.
Forms
When the quadratic polynomial has only one variable (univariate
In mathematics, a univariate object is an expression, equation, function or polynomial involving only one variable. Objects involving more than one variable are multivariate. In some cases the distinction between the univariate and multivariate ...
), one can distinguish its four main forms:
* The general form: where
* The factored form used for the logistic map
The logistic map is a polynomial mapping (equivalently, recurrence relation) of degree 2, often referred to as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations. The map was popula ...
:
* which has an indifferent fixed point with multiplier at the origin
Origin(s) or The Origin may refer to:
Arts, entertainment, and media
Comics and manga
* Origin (comics), ''Origin'' (comics), a Wolverine comic book mini-series published by Marvel Comics in 2002
* The Origin (Buffy comic), ''The Origin'' (Bu ...
* The monic and centered form,
The monic and centered form has been studied extensively, and has the following properties:
* It is the simplest form of a nonlinear
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many oth ...
function with one coefficient (parameter
A parameter (), generally, is any characteristic that can help in defining or classifying a particular system (meaning an event, project, object, situation, etc.). That is, a parameter is an element of a system that is useful, or critical, when ...
),
* It is a centered polynomial (the sum of its critical points is zero).
* it is a binomial
Binomial may refer to:
In mathematics
*Binomial (polynomial), a polynomial with two terms
*Binomial coefficient, numbers appearing in the expansions of powers of binomials
*Binomial QMF, a perfect-reconstruction orthogonal wavelet decomposition
* ...
The lambda form is:
* the simplest non-trivial perturbation of unperturbated system
* "the first family of dynamical system
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water i ...
s in which explicit necessary and sufficient conditions are known for when a small divisor problem is stable"
Conjugation
Between forms
Since isaffine
Affine may describe any of various topics concerned with connections or affinities.
It may refer to:
* Affine, a relative by marriage in law and anthropology
* Affine cipher, a special case of the more general substitution cipher
* Affine comb ...
conjugate to the general form of the quadratic polynomial it is often used to study complex dynamics
Complex dynamics is the study of dynamical systems defined by iteration of functions on complex number spaces. Complex analytic dynamics is the study of the dynamics of specifically analytic functions.
Techniques
*General
**Montel's theorem
** P ...
and to create images of Mandelbrot, Julia
Julia is usually a feminine given name. It is a Latinate feminine form of the name Julio and Julius. (For further details on etymology, see the Wiktionary entry "Julius".) The given name ''Julia'' had been in use throughout Late Antiquity (e.g ...
and Fatou sets.
When one wants change from to :
:
When one wants change from to , the parameter transformation is
:
and the transformation between the variables in and is
:
With doubling map
There is semi-conjugacy between the dyadic transformation (the doubling map) and the quadratic polynomial case of ''c'' = –2.Notation
Iteration
Here denotes the ''n''-thiterate
Iteration is the repetition of a process in order to generate a (possibly unbounded) sequence of outcomes. Each repetition of the process is a single iteration, and the outcome of each iteration is then the starting point of the next iteration. ...
of the function :
:
so
:
Because of the possible confusion with exponentiation, some authors write for the ''n''th iterate of .
Parameter
The monic and centered form can be marked by: * the parameter * the external angle of the ray that lands: ** at ''c'' in Mandelbrot set on the parameter plane ** on the critical value:''z'' = ''c'' in Julia set on the dynamic plane so : : : Examples: * c is the landing point of the 1/6 external ray of theMandelbrot set
The Mandelbrot set () is the set of complex numbers c for which the function f_c(z)=z^2+c does not diverge to infinity when iterated from z=0, i.e., for which the sequence f_c(0), f_c(f_c(0)), etc., remains bounded in absolute value.
This ...
, and is z->z^2+i (where i^2=-1)
* c is the landing point the 5/14 external ray and is z->z^2+c with c = -1.23922555538957 + 0.412602181602004*i
Map
The monic and centered form, sometimes called the Douady-Hubbard family of quadratic polynomials, is typically used with variable andparameter
A parameter (), generally, is any characteristic that can help in defining or classifying a particular system (meaning an event, project, object, situation, etc.). That is, a parameter is an element of a system that is useful, or critical, when ...
:
:
When it is used as an evolution function
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a ...
of the discrete nonlinear dynamical system
:
it is named the quadratic map
A map is a symbolic depiction emphasizing relationships between elements of some space, such as objects, regions, or themes.
Many maps are static, fixed to paper or some other durable medium, while others are dynamic or interactive. Although ...
:
:
The Mandelbrot set
The Mandelbrot set () is the set of complex numbers c for which the function f_c(z)=z^2+c does not diverge to infinity when iterated from z=0, i.e., for which the sequence f_c(0), f_c(f_c(0)), etc., remains bounded in absolute value.
This ...
is the set of values of the parameter ''c'' for which the initial condition ''z''0 = 0 does not cause the iterates to diverge to infinity.
Critical items
Critical points
complex plane
A critical point of is a point on the dynamical plane such that thederivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. ...
vanishes:
:
Since
:
implies
:
we see that the only (finite) critical point of is the point .
is an initial point for Mandelbrot set
The Mandelbrot set () is the set of complex numbers c for which the function f_c(z)=z^2+c does not diverge to infinity when iterated from z=0, i.e., for which the sequence f_c(0), f_c(f_c(0)), etc., remains bounded in absolute value.
This ...
iteration.
For the quadratic family the critical point z = 0 is the center of symmetry of the Julia set
In the context of complex dynamics, a branch of mathematics, the Julia set and the Fatou set are two complementary sets (Julia "laces" and Fatou "dusts") defined from a function. Informally, the Fatou set of the function consists of values wi ...
Jc, so it is a convex
Convex or convexity may refer to:
Science and technology
* Convex lens, in optics
Mathematics
* Convex set, containing the whole line segment that joins points
** Convex polygon, a polygon which encloses a convex set of points
** Convex polytop ...
combination of two points in Jc.
extended complex plane
In theRiemann sphere
In mathematics, the Riemann sphere, named after Bernhard Riemann, is a model of the extended complex plane: the complex plane plus one point at infinity. This extended plane represents the extended complex numbers, that is, the complex numbers ...
polynomial has 2d-2 critical points. Here zero and infinity
Infinity is that which is boundless, endless, or larger than any natural number. It is often denoted by the infinity symbol .
Since the time of the ancient Greeks, the philosophical nature of infinity was the subject of many discussions am ...
are critical points.
Critical value
A critical value of is the image of a critical point: : Since : we have : So the parameter is the critical value of .Critical level curves
A critical level curve the level curve which contain critical point. It acts as a sort of skeleton of dynamical plane Example : level curves cross atsaddle point
In mathematics, a saddle point or minimax point is a point on the surface of the graph of a function where the slopes (derivatives) in orthogonal directions are all zero (a critical point), but which is not a local extremum of the functi ...
, which is a special type of critical point.
Critical limit set
Critical limit set is the set of forward orbit of all critical pointsCritical orbit



 The forward orbit of a critical point is called a critical orbit. Critical orbits are very important because every attracting
The forward orbit of a critical point is called a critical orbit. Critical orbits are very important because every attracting periodic orbit In mathematics, in the study of iterated functions and dynamical systems, a periodic point of a function is a point which the system returns to after a certain number of function iterations or a certain amount of time.
Iterated functions
Given a ...
attracts a critical point, so studying the critical orbits helps us understand the dynamics in the Fatou set.
:
:
:
:
::
This orbit falls into an attracting periodic cycle if one exists.
Critical sector
The critical sector is a sector of the dynamical plane containing the critical point.Critical set
Critical set is a set of critical pointsCritical polynomial
: so : : : : These polynomials are used for: * finding centers of these Mandelbrot set components of period ''n''. Centers areroots
A root is the part of a plant, generally underground, that anchors the plant body, and absorbs and stores water and nutrients.
Root or roots may also refer to:
Art, entertainment, and media
* ''The Root'' (magazine), an online magazine focusing ...
of ''n''-th critical polynomials
::
* finding roots of Mandelbrot set components of period ''n'' (local minimum
In mathematical analysis, the maxima and minima (the respective plurals of maximum and minimum) of a function, known collectively as extrema (the plural of extremum), are the largest and smallest value of the function, either within a given ran ...
of )
* Misiurewicz points
::
Critical curves
 Diagrams of critical polynomials are called critical curves.
These curves create the skeleton (the dark lines) of a
Diagrams of critical polynomials are called critical curves.
These curves create the skeleton (the dark lines) of a bifurcation diagram
In mathematics, particularly in dynamical systems, a bifurcation diagram shows the values visited or approached asymptotically (fixed points, periodic orbits, or chaotic attractors) of a system as a function of a bifurcation parameter in the sy ...
.
Spaces, planes
4D space
One can use the Julia-Mandelbrot 4-dimension
In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coord ...
al (4D) space for a global analysis of this dynamical system.
 In this space there are two basic types of 2D planes:
* the dynamical (dynamic) plane, -plane or ''c''-plane
* the parameter plane or ''z''-plane
There is also another plane used to analyze such dynamical systems ''w''-plane:
* the conjugation plane
* model plane
In this space there are two basic types of 2D planes:
* the dynamical (dynamic) plane, -plane or ''c''-plane
* the parameter plane or ''z''-plane
There is also another plane used to analyze such dynamical systems ''w''-plane:
* the conjugation plane
* model plane
2D Parameter plane
Mandelbrot set
The Mandelbrot set () is the set of complex numbers c for which the function f_c(z)=z^2+c does not diverge to infinity when iterated from z=0, i.e., for which the sequence f_c(0), f_c(f_c(0)), etc., remains bounded in absolute value.
This ...
** The bifurcation locus = boundary of Mandelbrot set
The Mandelbrot set () is the set of complex numbers c for which the function f_c(z)=z^2+c does not diverge to infinity when iterated from z=0, i.e., for which the sequence f_c(0), f_c(f_c(0)), etc., remains bounded in absolute value.
This ...
with
*** root points
** Bounded hyperbolic components of the Mandelbrot set = interior of Mandelbrot set with internal rays
* exterior of Mandelbrot set with
** external rays
** equipotential lines
There are many different subtypes of the parameter plane.
 See also :
* Boettcher map which maps exterior of Mandelbrot set to the exterior of unit disc
* multiplier map which maps interior of hyperbolic component of Mandelbrot set to the interior of unit disc
See also :
* Boettcher map which maps exterior of Mandelbrot set to the exterior of unit disc
* multiplier map which maps interior of hyperbolic component of Mandelbrot set to the interior of unit disc
2D Dynamical plane
"The polynomial Pc maps each dynamical ray to another ray doubling the angle (which we measure in full turns, i.e. 0 = 1 = 2π rad = 360°), and the dynamical rays of any polynomial “look like straight rays” near infinity. This allows us to study the Mandelbrot and Julia sets combinatorially, replacing the dynamical plane by the unit circle, rays by angles, and the quadratic polynomial by the doubling modulo one map." Virpi KaukoOn the dynamical plane one can find: * The
Julia set
In the context of complex dynamics, a branch of mathematics, the Julia set and the Fatou set are two complementary sets (Julia "laces" and Fatou "dusts") defined from a function. Informally, the Fatou set of the function consists of values wi ...
* The Filled Julia set
* The Fatou set
* Orbits
The dynamical plane consists of:
* Fatou set
* Julia set
In the context of complex dynamics, a branch of mathematics, the Julia set and the Fatou set are two complementary sets (Julia "laces" and Fatou "dusts") defined from a function. Informally, the Fatou set of the function consists of values wi ...
Here, is a constant and is a variable.
The two-dimensional dynamical plane can be treated as a Poincaré cross-section of three-dimensional space of continuous dynamical system.
Dynamical ''z''-planes can be divided into two groups:
* plane for (see complex squaring map)
* planes (all other planes for )
Riemann sphere
The extended complex plane plus apoint at infinity
In geometry, a point at infinity or ideal point is an idealized limiting point at the "end" of each line.
In the case of an affine plane (including the Euclidean plane), there is one ideal point for each pencil of parallel lines of the plane. ...
* the Riemann sphere
Derivatives
First derivative with respect to ''c''
On the parameter plane: * is a variable * is constant The firstderivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. ...
of with respect to ''c'' is
:
This derivative can be found by iteration
Iteration is the repetition of a process in order to generate a (possibly unbounded) sequence of outcomes. Each repetition of the process is a single iteration, and the outcome of each iteration is then the starting point of the next iteration. ...
starting with
:
and then replacing at every consecutive step
:
This can easily be verified by using the chain rule
In calculus, the chain rule is a formula that expresses the derivative of the composition of two differentiable functions and in terms of the derivatives of and . More precisely, if h=f\circ g is the function such that h(x)=f(g(x)) for every , ...
for the derivative.
This derivative is used in the distance estimation method for drawing a Mandelbrot set.
First derivative with respect to ''z''
On the dynamical plane: * is a variable; * is a constant. At a fixed point , : At aperiodic point In mathematics, in the study of iterated functions and dynamical systems, a periodic point of a function is a point which the system returns to after a certain number of function iterations or a certain amount of time.
Iterated functions
Given a ...
''z''0 of period ''p'' the first derivative of a function
:
is often represented by and referred to as the multiplier or the Lyapunov characteristic number. Its logarithm
In mathematics, the logarithm is the inverse function to exponentiation. That means the logarithm of a number to the base is the exponent to which must be raised, to produce . For example, since , the ''logarithm base'' 10 ...
is known as the Lyapunov exponent. Absolute value of multiplier is used to check the stability
Stability may refer to:
Mathematics
*Stability theory, the study of the stability of solutions to differential equations and dynamical systems
** Asymptotic stability
** Linear stability
** Lyapunov stability
** Orbital stability
** Structural sta ...
of periodic (also fixed) points.
At a nonperiodic point, the derivative, denoted by , can be found by iteration
Iteration is the repetition of a process in order to generate a (possibly unbounded) sequence of outcomes. Each repetition of the process is a single iteration, and the outcome of each iteration is then the starting point of the next iteration. ...
starting with
:
and then using
:
This derivative is used for computing the external distance to the Julia set.
Schwarzian derivative
TheSchwarzian derivative
In mathematics, the Schwarzian derivative is an operator similar to the derivative which is invariant under Möbius transformations. Thus, it occurs in the theory of the complex projective line, and in particular, in the theory of modular forms an ...
(SD for short) of ''f'' is:/ref> :
See also
* Misiurewicz point * Periodic points of complex quadratic mappings *Mandelbrot set
The Mandelbrot set () is the set of complex numbers c for which the function f_c(z)=z^2+c does not diverge to infinity when iterated from z=0, i.e., for which the sequence f_c(0), f_c(f_c(0)), etc., remains bounded in absolute value.
This ...
*Julia set
In the context of complex dynamics, a branch of mathematics, the Julia set and the Fatou set are two complementary sets (Julia "laces" and Fatou "dusts") defined from a function. Informally, the Fatou set of the function consists of values wi ...
*Milnor–Thurston kneading theory The Milnor–Thurston kneading theory is a mathematics, mathematical theory which analyzes the iterates of piecewise monotone map (mathematics), mappings of an interval (mathematics), interval into itself. The emphasis is on understanding the proper ...
* Tent map
*Logistic map
The logistic map is a polynomial mapping (equivalently, recurrence relation) of degree 2, often referred to as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations. The map was popula ...
References
External links
* Monica Nevins and Thomas D. Rogers,Quadratic maps as dynamical systems on the p-adic numbers
Wolf Jung : Homeomorphisms on Edges of the Mandelbrot Set. Ph.D. thesis of 2002
*More about Quadratic Maps : https://mathworld.wolfram.com/QuadraticMap.html {{DEFAULTSORT:Complex Quadratic Polynomial Complex dynamics Fractals Polynomials