Complex Numbers on:
[Wikipedia]
[Google]
[Amazon]
 In mathematics, a complex number is an element of a number system that extends the
In mathematics, a complex number is an element of a number system that extends the
 A complex number is a number of the form , where and are
A complex number is a number of the form , where and are
 A complex number can thus be identified with an
A complex number can thus be identified with an

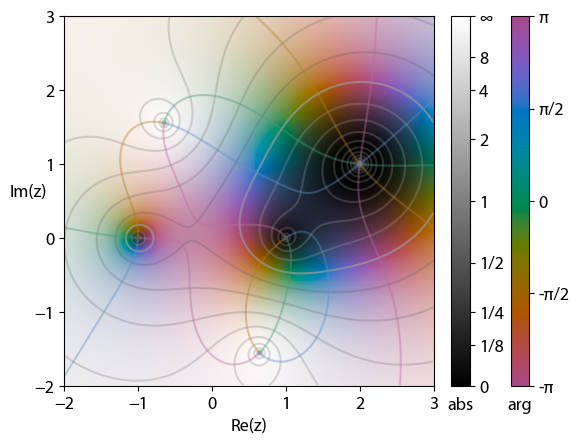 When visualizing complex functions, both a complex input and output are needed. Because each complex number is represented in two dimensions, visually graphing a complex function would require the perception of a
When visualizing complex functions, both a complex input and output are needed. Because each complex number is represented in two dimensions, visually graphing a complex function would require the perception of a
 The ''
The ''
 Two complex numbers and are most easily added by separately adding their real and imaginary parts. That is to say:
Similarly, subtraction can be performed as
Multiplication of a complex number and a real number can be done similarly by multiplying separately and the real and imaginary parts of :
In particular, subtraction can be done by negating the subtrahend (that is multiplying it with ) and adding the result to the minuend:
Using the visualization of complex numbers in the complex plane, addition has the following geometric interpretation: the sum of two complex numbers and , interpreted as points in the complex plane, is the point obtained by building a parallelogram from the three vertices , and the points of the arrows labeled and (provided that they are not on a line). Equivalently, calling these points , , respectively and the fourth point of the parallelogram the
Two complex numbers and are most easily added by separately adding their real and imaginary parts. That is to say:
Similarly, subtraction can be performed as
Multiplication of a complex number and a real number can be done similarly by multiplying separately and the real and imaginary parts of :
In particular, subtraction can be done by negating the subtrahend (that is multiplying it with ) and adding the result to the minuend:
Using the visualization of complex numbers in the complex plane, addition has the following geometric interpretation: the sum of two complex numbers and , interpreted as points in the complex plane, is the point obtained by building a parallelogram from the three vertices , and the points of the arrows labeled and (provided that they are not on a line). Equivalently, calling these points , , respectively and the fourth point of the parallelogram the
 Formulas for multiplication, division and exponentiation are simpler in polar form than the corresponding formulas in Cartesian coordinates. Given two complex numbers and , because of the trigonometric identities
we may derive
In other words, the absolute values are multiplied and the arguments are added to yield the polar form of the product. For example, multiplying by corresponds to a quarter-
Formulas for multiplication, division and exponentiation are simpler in polar form than the corresponding formulas in Cartesian coordinates. Given two complex numbers and , because of the trigonometric identities
we may derive
In other words, the absolute values are multiplied and the arguments are added to yield the polar form of the product. For example, multiplying by corresponds to a quarter-
real number
In mathematics, a real number is a number that can be used to measurement, measure a ''continuous'' one-dimensional quantity such as a distance, time, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small var ...
s with a specific element denoted , called the imaginary unit
The imaginary unit or unit imaginary number () is a solution to the quadratic equation x^2+1=0. Although there is no real number with this property, can be used to extend the real numbers to what are called complex numbers, using addition a ...
and satisfying the equation ; every complex number can be expressed in the form , where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes
René Descartes ( or ; ; Latinized: Renatus Cartesius; 31 March 1596 – 11 February 1650) was a French philosopher, scientist, and mathematician, widely considered a seminal figure in the emergence of modern philosophy and science. Mathe ...
. For the complex number , is called the , and is called the . The set of complex numbers is denoted by either of the symbols or . Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers and are fundamental in many aspects of the scientific description of the natural world.
Complex numbers allow solutions to all polynomial equation
In mathematics, an algebraic equation or polynomial equation is an equation of the form
:P = 0
where ''P'' is a polynomial with coefficients in some field, often the field of the rational numbers. For many authors, the term ''algebraic equati ...
s, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real or complex coefficients has a solution which is a complex number. For example, the equation
has no real solution, since the square of a real number cannot be negative, but has the two nonreal complex solutions and .
Addition, subtraction and multiplication of complex numbers can be naturally defined by using the rule combined with the associative, commutative, and distributive laws. Every nonzero complex number has a multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number ''x'', denoted by 1/''x'' or ''x''−1, is a number which when multiplied by ''x'' yields the multiplicative identity, 1. The multiplicative inverse of a fraction ''a''/''b ...
. This makes the complex numbers a field that has the real numbers as a subfield. The complex numbers also form a real vector space of dimension two, with as a standard basis.
This standard basis makes the complex numbers a Cartesian plane, called the complex plane
In mathematics, the complex plane is the plane formed by the complex numbers, with a Cartesian coordinate system such that the -axis, called the real axis, is formed by the real numbers, and the -axis, called the imaginary axis, is formed by th ...
. This allows a geometric interpretation of the complex numbers and their operations, and conversely expressing in terms of complex numbers some geometric properties and constructions. For example, the real numbers form the real line
In elementary mathematics, a number line is a picture of a graduated straight line that serves as visual representation of the real numbers. Every point of a number line is assumed to correspond to a real number, and every real number to a po ...
which is identified to the horizontal axis of the complex plane. The complex numbers of absolute value one form the unit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucli ...
. The addition of a complex number is a translation
Translation is the communication of the Meaning (linguistic), meaning of a #Source and target languages, source-language text by means of an Dynamic and formal equivalence, equivalent #Source and target languages, target-language text. The ...
in the complex plane, and the multiplication by a complex number is a similarity centered at the origin. The complex conjugation is the reflection symmetry with respect to the real axis. The complex absolute value is a Euclidean norm.
In summary, the complex numbers form a rich structure that is simultaneously an algebraically closed field, a commutative algebra
Commutative algebra, first known as ideal theory, is the branch of algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra. Promi ...
over the reals, and a Euclidean vector space of dimension two.
Definition
real numbers
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every ...
, and is an indeterminate satisfying . For example, is a complex number.
This way, a complex number is defined as a polynomial
In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An ex ...
with real coefficients in the single indeterminate , for which the relation is imposed. Based on this definition, complex numbers can be added and multiplied, using the addition and multiplication for polynomials. The relation induces the equalities and which hold for all integers ; these allow the reduction of any polynomial that results from the addition and multiplication of complex numbers to a linear polynomial in , again of the form with real coefficients
The real number is called the ''real part'' of the complex number ; the real number is called its ''imaginary part''. To emphasize, the imaginary part does not include a factor ; that is, the imaginary part is , not .
Formally, the complex numbers are defined as the quotient ring of the polynomial ring in the indeterminate , by the ideal generated by the polynomial (see below
Below may refer to:
*Earth
* Ground (disambiguation)
* Soil
* Floor
* Bottom (disambiguation)
* Less than
*Temperatures below freezing
* Hell or underworld
People with the surname
* Ernst von Below (1863–1955), German World War I general
* Fr ...
).
Notation
A real number can be regarded as a complex number , whose imaginary part is 0. A purely imaginary number is a complex number , whose real part is zero. As with polynomials, it is common to write for and for . Moreover, when the imaginary part is negative, that is, , it is common to write instead of ; for example, for , can be written instead of . Since the multiplication of the indeterminate and a real is commutative in polynomials with real coefficients, the polynomial may be written as This is often expedient for imaginary parts denoted by expressions, for example, when is a radical. The real part of a complex number is denoted by , , or ; the imaginary part of a complex number is denoted by , , or For example, The set of all complex numbers is denoted by ( blackboard bold) or (upright bold). In some disciplines, particularly inelectromagnetism
In physics, electromagnetism is an interaction that occurs between particles with electric charge. It is the second-strongest of the four fundamental interactions, after the strong force, and it is the dominant force in the interactions o ...
and electrical engineering, is used instead of as is frequently used to represent electric current
An electric current is a stream of charged particles, such as electrons or ions, moving through an electrical conductor or space. It is measured as the net rate of flow of electric charge through a surface or into a control volume. The movin ...
. In these cases, complex numbers are written as , or .
Visualization
ordered pair
In mathematics, an ordered pair (''a'', ''b'') is a pair of objects. The order in which the objects appear in the pair is significant: the ordered pair (''a'', ''b'') is different from the ordered pair (''b'', ''a'') unless ''a'' = ''b''. (In co ...
of real numbers, which in turn may be interpreted as coordinates of a point in a two-dimensional space. The most immediate space is the Euclidean plane with suitable coordinates, which is then called ''complex plane'' or '' Argand diagram,'' named after Jean-Robert Argand. Another prominent space on which the coordinates may be projected is the two-dimensional surface of a sphere, which is then called Riemann sphere.
Cartesian complex plane
The definition of the complex numbers involving two arbitrary real values immediately suggests the use of Cartesian coordinates in the complex plane. The horizontal (''real'') axis is generally used to display the real part, with increasing values to the right, and the imaginary part marks the vertical (''imaginary'') axis, with increasing values upwards. A charted number may be viewed either as the coordinatized point or as a position vector from the origin to this point. The coordinate values of a complex number can hence be expressed in its ''Cartesian'', ''rectangular'', or ''algebraic'' form. Notably, the operations of addition and multiplication take on a very natural geometric character, when complex numbers are viewed as position vectors: addition corresponds to vector addition, while multiplication (seebelow
Below may refer to:
*Earth
* Ground (disambiguation)
* Soil
* Floor
* Bottom (disambiguation)
* Less than
*Temperatures below freezing
* Hell or underworld
People with the surname
* Ernst von Below (1863–1955), German World War I general
* Fr ...
) corresponds to multiplying their magnitudes and adding the angles they make with the real axis. Viewed in this way, the multiplication of a complex number by corresponds to rotating the position vector counterclockwise
Two-dimensional rotation can occur in two possible directions. Clockwise motion (abbreviated CW) proceeds in the same direction as a clock's hands: from the top to the right, then down and then to the left, and back up to the top. The opposite s ...
by a quarter turn
Turn may refer to:
Arts and entertainment
Dance and sports
* Turn (dance and gymnastics), rotation of the body
* Turn (swimming), reversing direction at the end of a pool
* Turn (professional wrestling), a transition between face and heel
* Turn, ...
( 90°) about the origin—a fact which can be expressed algebraically as follows:
Polar complex plane
Modulus and argument
An alternative option for coordinates in the complex plane is thepolar coordinate system
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point (analogous to th ...
that uses the distance of the point from the origin
Origin(s) or The Origin may refer to:
Arts, entertainment, and media
Comics and manga
* ''Origin'' (comics), a Wolverine comic book mini-series published by Marvel Comics in 2002
* ''The Origin'' (Buffy comic), a 1999 ''Buffy the Vampire Sl ...
(), and the angle subtended between the positive real axis and the line segment in a counterclockwise sense. This leads to the polar form
:
of a complex number, where is the absolute value of , and is the argument
An argument is a statement or group of statements called premises intended to determine the degree of truth or acceptability of another statement called conclusion. Arguments can be studied from three main perspectives: the logical, the dialect ...
of .
The ''absolute value'' (or ''modulus'' or ''magnitude'') of a complex number is
If is a real number (that is, if ), then . That is, the absolute value of a real number equals its absolute value as a complex number.
By Pythagoras' theorem, the absolute value of a complex number is the distance to the origin of the point representing the complex number in the complex plane
In mathematics, the complex plane is the plane formed by the complex numbers, with a Cartesian coordinate system such that the -axis, called the real axis, is formed by the real numbers, and the -axis, called the imaginary axis, is formed by th ...
.
The ''argument'' of (in many applications referred to as the "phase" ) is the angle of the radius
In classical geometry, a radius ( : radii) of a circle or sphere is any of the line segments from its center to its perimeter, and in more modern usage, it is also their length. The name comes from the latin ''radius'', meaning ray but also the ...
with the positive real axis, and is written as . As with the modulus, the argument can be found from the rectangular form —by applying the inverse tangent to the quotient of imaginary-by-real parts. By using a half-angle identity, a single branch of the arctan suffices to cover the range of the -function, and avoids a more subtle case-by-case analysis
Normally, as given above, the principal value in the interval is chosen. If the arg value is negative, values in the range or can be obtained by adding . The value of is expressed in radians in this article. It can increase by any integer multiple of and still give the same angle, viewed as subtended by the rays of the positive real axis and from the origin through . Hence, the arg function is sometimes considered as multivalued. The polar angle for the complex number 0 is indeterminate, but arbitrary choice of the polar angle 0 is common.
The value of equals the result of atan2:
Together, and give another way of representing complex numbers, the ''polar form'', as the combination of modulus and argument fully specify the position of a point on the plane. Recovering the original rectangular co-ordinates from the polar form is done by the formula called ''trigonometric form''
Using Euler's formula this can be written as
Using the function, this is sometimes abbreviated to
In angle notation, often used in electronics
The field of electronics is a branch of physics and electrical engineering that deals with the emission, behaviour and effects of electrons using electronic devices. Electronics uses active devices to control electron flow by amplification ...
to represent a phasor with amplitude and phase , it is written as
Complex graphs
 When visualizing complex functions, both a complex input and output are needed. Because each complex number is represented in two dimensions, visually graphing a complex function would require the perception of a
When visualizing complex functions, both a complex input and output are needed. Because each complex number is represented in two dimensions, visually graphing a complex function would require the perception of a four dimensional space
A four-dimensional space (4D) is a mathematical extension of the concept of three-dimensional or 3D space. Three-dimensional space is the simplest possible abstraction of the observation that one only needs three numbers, called ''dimensions'', ...
, which is possible only in projections. Because of this, other ways of visualizing complex functions have been designed.
In domain coloring the output dimensions are represented by color and brightness, respectively. Each point in the complex plane as domain is ''ornated'', typically with ''color'' representing the argument of the complex number, and ''brightness'' representing the magnitude. Dark spots mark moduli near zero, brighter spots are farther away from the origin, the gradation may be discontinuous, but is assumed as monotonous. The colors often vary in steps of for to from red, yellow, green, cyan, blue, to magenta. These plots are called color wheel graphs. This provides a simple way to visualize the functions without losing information. The picture shows zeros for and poles at
History
The solution inradicals
Radical may refer to:
Politics and ideology Politics
*Radical politics, the political intent of fundamental societal change
*Radicalism (historical), the Radical Movement that began in late 18th century Britain and spread to continental Europe and ...
(without trigonometric functions) of a general cubic equation, when all three of its roots are real numbers, contains the square roots of negative numbers, a situation that cannot be rectified by factoring aided by the rational root test, if the cubic is irreducible; this is the so-called '' casus irreducibilis'' ("irreducible case"). This conundrum led Italian mathematician Gerolamo Cardano
Gerolamo Cardano (; also Girolamo or Geronimo; french: link=no, Jérôme Cardan; la, Hieronymus Cardanus; 24 September 1501– 21 September 1576) was an Italian polymath, whose interests and proficiencies ranged through those of mathematician, ...
to conceive of complex numbers in around 1545 in his ''Ars Magna'', though his understanding was rudimentary; moreover he later dismissed complex numbers as "subtle as they are useless". Cardano did use imaginary numbers, but described using them as “mental torture.” This was prior to the use of the graphical complex plane. Cardano and other Italian mathematicians, notably Scipione del Ferro, in the 1500s created an algorithm for solving cubic equations which generally had one real solution and two solutions containing an imaginary number. Since they ignored the answers with the imaginary numbers, Cardano found them useless.
Work on the problem of general polynomials ultimately led to the fundamental theorem of algebra, which shows that with complex numbers, a solution exists to every polynomial equation
In mathematics, an algebraic equation or polynomial equation is an equation of the form
:P = 0
where ''P'' is a polynomial with coefficients in some field, often the field of the rational numbers. For many authors, the term ''algebraic equati ...
of degree one or higher. Complex numbers thus form an algebraically closed field, where any polynomial equation has a root
In vascular plants, the roots are the organs of a plant that are modified to provide anchorage for the plant and take in water and nutrients into the plant body, which allows plants to grow taller and faster. They are most often below the sur ...
.
Many mathematicians contributed to the development of complex numbers. The rules for addition, subtraction, multiplication, and root extraction of complex numbers were developed by the Italian mathematician Rafael Bombelli. A more abstract formalism for the complex numbers was further developed by the Irish mathematician William Rowan Hamilton
Sir William Rowan Hamilton LL.D, DCL, MRIA, FRAS (3/4 August 1805 – 2 September 1865) was an Irish mathematician, astronomer, and physicist. He was the Andrews Professor of Astronomy at Trinity College Dublin, and Royal Astronomer of Ire ...
, who extended this abstraction to the theory of quaternions
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. Hamilton defined a quatern ...
.
The earliest fleeting reference to square root
In mathematics, a square root of a number is a number such that ; in other words, a number whose ''square'' (the result of multiplying the number by itself, or ⋅ ) is . For example, 4 and −4 are square roots of 16, because .
...
s of negative number
In mathematics, a negative number represents an opposite. In the real number system, a negative number is a number that is inequality (mathematics), less than 0 (number), zero. Negative numbers are often used to represent the magnitude of a loss ...
s can perhaps be said to occur in the work of the Greek mathematician
Greek mathematics refers to mathematics texts and ideas stemming from the Archaic through the Hellenistic and Roman periods, mostly extant from the 7th century BC to the 4th century AD, around the shores of the Eastern Mediterranean. Greek mathem ...
Hero of Alexandria
Hero of Alexandria (; grc-gre, Ἥρων ὁ Ἀλεξανδρεύς, ''Heron ho Alexandreus'', also known as Heron of Alexandria ; 60 AD) was a Greek mathematician and engineer who was active in his native city of Alexandria, Roman Egypt. He ...
in the 1st century AD, where in his '' Stereometrica'' he considered, apparently in error, the volume of an impossible frustum of a pyramid
A pyramid (from el, πυραμίς ') is a structure whose outer surfaces are triangular and converge to a single step at the top, making the shape roughly a pyramid in the geometric sense. The base of a pyramid can be trilateral, quadrila ...
to arrive at the term in his calculations, which today would simplify to . Negative quantities were not conceived of in Hellenistic mathematics
Greek mathematics refers to mathematics texts and ideas stemming from the Archaic through the Hellenistic and Roman periods, mostly extant from the 7th century BC to the 4th century AD, around the shores of the Eastern Mediterranean. Greek math ...
and Hero merely replaced it by its positive
The impetus to study complex numbers as a topic in itself first arose in the 16th century when algebraic solutions for the roots of cubic
Cubic may refer to:
Science and mathematics
* Cube (algebra), "cubic" measurement
* Cube, a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex
** Cubic crystal system, a crystal system w ...
and quartic polynomial
In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An ex ...
s were discovered by Italian mathematicians (see Niccolò Fontana Tartaglia, Gerolamo Cardano
Gerolamo Cardano (; also Girolamo or Geronimo; french: link=no, Jérôme Cardan; la, Hieronymus Cardanus; 24 September 1501– 21 September 1576) was an Italian polymath, whose interests and proficiencies ranged through those of mathematician, ...
). It was soon realized (but proved much later) that these formulas, even if one were interested only in real solutions, sometimes required the manipulation of square roots of negative numbers. As an example, Tartaglia's formula for a cubic equation of the form gives the solution to the equation as
At first glance this looks like nonsense. However, formal calculations with complex numbers show that the equation has three solutions: Substituting these in turn for in Tartaglia's cubic formula and simplifying, one gets 0, 1 and −1 as the solutions of . Of course this particular equation can be solved at sight but it does illustrate that when general formulas are used to solve cubic equations with real roots then, as later mathematicians showed rigorously, the use of complex numbers is unavoidable. Rafael Bombelli was the first to address explicitly these seemingly paradoxical solutions of cubic equations and developed the rules for complex arithmetic trying to resolve these issues.
The term "imaginary" for these quantities was coined by René Descartes
René Descartes ( or ; ; Latinized: Renatus Cartesius; 31 March 1596 – 11 February 1650) was a French philosopher, scientist, and mathematician, widely considered a seminal figure in the emergence of modern philosophy and science. Mathe ...
in 1637, who was at pains to stress their unreal nature
A further source of confusion was that the equation seemed to be capriciously inconsistent with the algebraic identity , which is valid for non-negative real numbers and , and which was also used in complex number calculations with one of , positive and the other negative. The incorrect use of this identity (and the related identity ) in the case when both and are negative even bedeviled Leonhard Euler
Leonhard Euler ( , ; 15 April 170718 September 1783) was a Swiss mathematician, physicist, astronomer, geographer, logician and engineer who founded the studies of graph theory and topology and made pioneering and influential discoveries in ma ...
. This difficulty eventually led to the convention of using the special symbol in place of to guard against this mistake. Even so, Euler considered it natural to introduce students to complex numbers much earlier than we do today. In his elementary algebra text book, '' Elements of Algebra'', he introduces these numbers almost at once and then uses them in a natural way throughout.
In the 18th century complex numbers gained wider use, as it was noticed that formal manipulation of complex expressions could be used to simplify calculations involving trigonometric functions. For instance, in 1730 Abraham de Moivre noted that the identities relating trigonometric functions of an integer multiple of an angle to powers of trigonometric functions of that angle could be re-expressed by the following de Moivre's formula:
In 1748, Euler went further and obtained Euler's formula of complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is helpful in many branches of mathematics, including algebra ...
:
by formally manipulating complex power series
In mathematics, a power series (in one variable) is an infinite series of the form
\sum_^\infty a_n \left(x - c\right)^n = a_0 + a_1 (x - c) + a_2 (x - c)^2 + \dots
where ''an'' represents the coefficient of the ''n''th term and ''c'' is a con ...
and observed that this formula could be used to reduce any trigonometric identity to much simpler exponential identities.
The idea of a complex number as a point in the complex plane ( above) was first described by Danish– Norwegian mathematician
A mathematician is someone who uses an extensive knowledge of mathematics in their work, typically to solve mathematical problems.
Mathematicians are concerned with numbers, data, quantity, mathematical structure, structure, space, Mathematica ...
Caspar Wessel in 1799, although it had been anticipated as early as 1685 in Wallis's ''A Treatise of Algebra''.
Wessel's memoir appeared in the Proceedings of the Copenhagen Academy
The Royal Danish Academy of Fine Arts ( da, Det Kongelige Danske Kunstakademi - Billedkunst Skolerne) has provided education in the arts for more than 250 years, playing its part in the development of the art of Denmark.
History
The Royal Dani ...
but went largely unnoticed. In 1806 Jean-Robert Argand independently issued a pamphlet on complex numbers and provided a rigorous proof of the fundamental theorem of algebra. Carl Friedrich Gauss
Johann Carl Friedrich Gauss (; german: Gauß ; la, Carolus Fridericus Gauss; 30 April 177723 February 1855) was a German mathematician and physicist who made significant contributions to many fields in mathematics and science. Sometimes refe ...
had earlier published an essentially topological proof of the theorem in 1797 but expressed his doubts at the time about "the true metaphysics of the square root of −1". It was not until 1831 that he overcame these doubts and published his treatise on complex numbers as points in the plane, largely establishing modern notation and terminology:
If one formerly contemplated this subject from a false point of view and therefore found a mysterious darkness, this is in large part attributable to clumsy terminology. Had one not called +1, -1, positive, negative, or imaginary (or even impossible) units, but instead, say, direct, inverse, or lateral units, then there could scarcely have been talk of such darkness.In the beginning of the 19th century, other mathematicians discovered independently the geometrical representation of the complex numbers: Buée, Mourey, Warren, Français and his brother, Bellavitis. The English mathematician G.H. Hardy remarked that Gauss was the first mathematician to use complex numbers in 'a really confident and scientific way' although mathematicians such as Norwegian Niels Henrik Abel and Carl Gustav Jacob Jacobi were necessarily using them routinely before Gauss published his 1831 treatise.
Augustin-Louis Cauchy
Baron Augustin-Louis Cauchy (, ; ; 21 August 178923 May 1857) was a French mathematician, engineer, and physicist who made pioneering contributions to several branches of mathematics, including mathematical analysis and continuum mechanics. H ...
and Bernhard Riemann together brought the fundamental ideas of complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is helpful in many branches of mathematics, including algebra ...
to a high state of completion, commencing around 1825 in Cauchy's case.
The common terms used in the theory are chiefly due to the founders. Argand called the ''direction factor'', and the ''modulus''; Cauchy (1821) called the ''reduced form'' (l'expression réduite) and apparently introduced the term ''argument''; Gauss used for , introduced the term ''complex number'' for , and called the ''norm''. The expression ''direction coefficient'', often used for , is due to Hankel (1867), and ''absolute value,'' for ''modulus,'' is due to Weierstrass.
Later classical writers on the general theory include Richard Dedekind
Julius Wilhelm Richard Dedekind (6 October 1831 – 12 February 1916) was a German mathematician who made important contributions to number theory, abstract algebra (particularly ring theory), and
the axiomatic foundations of arithmetic. His ...
, Otto Hölder, Felix Klein
Christian Felix Klein (; 25 April 1849 – 22 June 1925) was a German mathematician and mathematics educator, known for his work with group theory, complex analysis, non-Euclidean geometry, and on the associations between geometry and grou ...
, Henri Poincaré
Jules Henri Poincaré ( S: stress final syllable ; 29 April 1854 – 17 July 1912) was a French mathematician, theoretical physicist, engineer, and philosopher of science. He is often described as a polymath, and in mathematics as "The ...
, Hermann Schwarz, Karl Weierstrass and many others. Important work (including a systematization) in complex multivariate calculus has been started at beginning of the 20th century. Important results have been achieved by Wilhelm Wirtinger in 1927.
Relations and operations
Equality
Complex numbers have a similar definition of equality to real numbers; two complex numbers and are equalif and only if
In logic and related fields such as mathematics and philosophy, "if and only if" (shortened as "iff") is a biconditional logical connective between statements, where either both statements are true or both are false.
The connective is bi ...
both their real and imaginary parts are equal, that is, if and . Nonzero complex numbers written in polar form are equal if and only if they have the same magnitude and their arguments differ by an integer multiple of .
Ordering
Unlike the real numbers, there is no natural ordering of the complex numbers. In particular, there is no linear ordering on the complex numbers that is compatible with addition and multiplication. Hence, the complex numbers do not have the structure of an ordered field. One explanation for this is that every non-trivial sum of squares in an ordered field is nonzero, and is a non-trivial sum of squares. Thus, complex numbers are naturally thought of as existing on a two-dimensional plane.Conjugate
complex conjugate
In mathematics, the complex conjugate of a complex number is the number with an equal real part and an imaginary part equal in magnitude but opposite in sign. That is, (if a and b are real, then) the complex conjugate of a + bi is equal to a - ...
'' of the complex number is given by . It is denoted by either or . This unary operation
In mathematics, an unary operation is an operation with only one operand, i.e. a single input. This is in contrast to binary operations, which use two operands. An example is any function , where is a set. The function is a unary operation ...
on complex numbers cannot be expressed by applying only their basic operations addition, subtraction, multiplication and division.
Geometrically, is the "reflection" of about the real axis. Conjugating twice gives the original complex number
which makes this operation an involution. The reflection leaves both the real part and the magnitude of unchanged, that is
and
The imaginary part and the argument of a complex number change their sign under conjugation
For details on argument and magnitude, see the section on Polar form.
The product of a complex number and its conjugate is known as the '' absolute square''. It is always a non-negative real number and equals the square of the magnitude of each:
This property can be used to convert a fraction with a complex denominator to an equivalent fraction with a real denominator by expanding both numerator and denominator of the fraction by the conjugate of the given denominator. This process is sometimes called " rationalization" of the denominator (although the denominator in the final expression might be an irrational real number), because it resembles the method to remove roots from simple expressions in a denominator.
The real and imaginary parts of a complex number can be extracted using the conjugation:
Moreover, a complex number is real if and only if it equals its own conjugate.
Conjugation distributes over the basic complex arithmetic operations:
Conjugation is also employed in inversive geometry, a branch of geometry studying reflections more general than ones about a line. In the network analysis of electrical circuits, the complex conjugate is used in finding the equivalent impedance when the maximum power transfer theorem is looked for.
Addition and subtraction
triangle
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices ''A'', ''B'', and ''C'' is denoted \triangle ABC.
In Euclidean geometry, any three points, when non- colli ...
s and are congruent.
Multiplication and square
The rules of the distributive property, the commutative properties (of addition and multiplication), and the defining property apply to complex numbers. It follows that In particular,Reciprocal and division
Using the conjugation, the reciprocal of a nonzero complex number can always be broken down to since ''non-zero'' implies that is greater than zero. This can be used to express a division of an arbitrary complex number by a non-zero complex number asMultiplication and division in polar form
turn
Turn may refer to:
Arts and entertainment
Dance and sports
* Turn (dance and gymnastics), rotation of the body
* Turn (swimming), reversing direction at the end of a pool
* Turn (professional wrestling), a transition between face and heel
* Turn, ...
counter-clockwise, which gives back . The picture at the right illustrates the multiplication of
Since the real and imaginary part of are equal, the argument of that number is 45 degrees, or (in radian). On the other hand, it is also the sum of the angles at the origin of the red and blue triangles are arctan
In mathematics, the inverse trigonometric functions (occasionally also called arcus functions, antitrigonometric functions or cyclometric functions) are the inverse functions of the trigonometric functions (with suitably restricted domains). S ...
(1/3) and arctan(1/2), respectively. Thus, the formula
holds. As the arctan
In mathematics, the inverse trigonometric functions (occasionally also called arcus functions, antitrigonometric functions or cyclometric functions) are the inverse functions of the trigonometric functions (with suitably restricted domains). S ...
function can be approximated highly efficiently, formulas like this – known as Machin-like formulas – are used for high-precision approximations of .
Similarly, division is given by
Square root
The square roots of (with ) are , where and where is the signum function. This can be seen by squaring to obtain . Here is called the modulus of , and the square root sign indicates the square root with non-negative real part, called the principal square root; also where .Exponential function
Theexponential function
The exponential function is a mathematical function denoted by f(x)=\exp(x) or e^x (where the argument is written as an exponent). Unless otherwise specified, the term generally refers to the positive-valued function of a real variable, ...
can be defined for every complex number by the power series
In mathematics, a power series (in one variable) is an infinite series of the form
\sum_^\infty a_n \left(x - c\right)^n = a_0 + a_1 (x - c) + a_2 (x - c)^2 + \dots
where ''an'' represents the coefficient of the ''n''th term and ''c'' is a con ...
which has an infinite radius of convergence.
The value at of the exponential function is Euler's number
If is real, one has
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of definition of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a n ...
allows extending this equality for every complex value of , and thus to define the complex exponentiation with base as
Functional equation
The exponential function satisfies the functional equation This can be proved either by comparing the power series expansion of both members or by applyinganalytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of definition of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a n ...
from the restriction of the equation to real arguments.
Euler's formula
Euler's formula states that, for any real number , The functional equation implies thus that, if and are real, one has which is the decomposition of the exponential function into its real and imaginary parts.Complex logarithm
In the real case, thenatural logarithm
The natural logarithm of a number is its logarithm to the base of the mathematical constant , which is an irrational and transcendental number approximately equal to . The natural logarithm of is generally written as , , or sometimes, if ...
can be defined as the inverse
Inverse or invert may refer to:
Science and mathematics
* Inverse (logic), a type of conditional sentence which is an immediate inference made from another conditional sentence
* Additive inverse (negation), the inverse of a number that, when ad ...
of the exponential function. For extending this to the complex domain, one can start from Euler's formula. It implies that, if a complex number is written in polar form
with then with
as complex logarithm one has a proper inverse:
However, because cosine and sine are periodic functions, the addition of an integer multiple of to does not change . For example, , so both and are possible values for the natural logarithm of .
Therefore, if the complex logarithm is not to be defined as a multivalued function
In mathematics, a multivalued function, also called multifunction, many-valued function, set-valued function, is similar to a function, but may associate several values to each input. More precisely, a multivalued function from a domain to ...
one has to use a branch cut and to restrict the codomain
In mathematics, the codomain or set of destination of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation . The term range is sometimes ambiguously used to refer to either ...
, resulting in the bijective
In mathematics, a bijection, also known as a bijective function, one-to-one correspondence, or invertible function, is a function between the elements of two sets, where each element of one set is paired with exactly one element of the other ...
function
If is not a non-positive real number (a positive or a non-real number), the resulting principal value of the complex logarithm is obtained with . It is an analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions. Functions of each type are infinitely differentiable, but complex ...
outside the negative real numbers, but it cannot be prolongated to a function that is continuous at any negative real number , where the principal value is .
Exponentiation
If is real and complex, the exponentiation is defined as where denotes the natural logarithm. It seems natural to extend this formula to complex values of , but there are some difficulties resulting from the fact that the complex logarithm is not really a function, but amultivalued function
In mathematics, a multivalued function, also called multifunction, many-valued function, set-valued function, is similar to a function, but may associate several values to each input. More precisely, a multivalued function from a domain to ...
.
It follows that if is as above, and if is another complex number, then the ''exponentiation'' is the multivalued function
Integer and fractional exponents
If, in the preceding formula, is an integer, then the sine and the cosine are independent of . Thus, if the exponent is an integer, then is well defined, and the exponentiation formula simplifies to de Moivre's formula: The th roots of a complex number are given by for . (Here is the usual (positive) th root of the positive real number .) Because sine and cosine are periodic, other integer values of do not give other values. While the th root of a positive real number is chosen to be the ''positive'' real number satisfying , there is no natural way of distinguishing one particular complex th root of a complex number. Therefore, the th root is a -valued function of . This implies that, contrary to the case of positive real numbers, one has since the left-hand side consists of values, and the right-hand side is a single value.Properties
Field structure
The set of complex numbers is a field. Briefly, this means that the following facts hold: first, any two complex numbers can be added and multiplied to yield another complex number. Second, for any complex number , its additive inverse is also a complex number; and third, every nonzero complex number has a reciprocal complex number. Moreover, these operations satisfy a number of laws, for example the law of commutativity of addition and multiplication for any two complex numbers and : These two laws and the other requirements on a field can be proven by the formulas given above, using the fact that the real numbers themselves form a field. Unlike the reals, is not an ordered field, that is to say, it is not possible to define a relation that is compatible with the addition and multiplication. In fact, in any ordered field, the square of any element is necessarily positive, so precludes the existence of an ordering on When the underlying field for a mathematical topic or construct is the field of complex numbers, the topic's name is usually modified to reflect that fact. For example:complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is helpful in many branches of mathematics, including algebra ...
, complex matrix
Matrix most commonly refers to:
* ''The Matrix'' (franchise), an American media franchise
** '' The Matrix'', a 1999 science-fiction action film
** "The Matrix", a fictional setting, a virtual reality environment, within ''The Matrix'' (franchi ...
, complex polynomial
In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An ex ...
, and complex Lie algebra
In mathematics, a Lie algebra (pronounced ) is a vector space \mathfrak g together with an operation called the Lie bracket, an alternating bilinear map \mathfrak g \times \mathfrak g \rightarrow \mathfrak g, that satisfies the Jacobi iden ...
.
Solutions of polynomial equations
Given any complex numbers (calledcoefficient
In mathematics, a coefficient is a multiplicative factor in some term of a polynomial, a series, or an expression; it is usually a number, but may be any expression (including variables such as , and ). When the coefficients are themselves ...
s) , the equation
has at least one complex solution ''z'', provided that at least one of the higher coefficients is nonzero. This is the statement of the fundamental theorem of algebra, of Carl Friedrich Gauss
Johann Carl Friedrich Gauss (; german: Gauß ; la, Carolus Fridericus Gauss; 30 April 177723 February 1855) was a German mathematician and physicist who made significant contributions to many fields in mathematics and science. Sometimes refe ...
and Jean le Rond d'Alembert
Jean-Baptiste le Rond d'Alembert (; ; 16 November 1717 – 29 October 1783) was a French mathematician, mechanician, physicist, philosopher, and music theorist. Until 1759 he was, together with Denis Diderot, a co-editor of the '' Encyclop� ...
. Because of this fact, is called an algebraically closed field. This property does not hold for the field of rational numbers (the polynomial does not have a rational root, since √2 is not a rational number) nor the real numbers (the polynomial does not have a real root for , since the square of is positive for any real number ).
There are various proofs of this theorem, by either analytic methods such as Liouville's theorem, or topological ones such as the winding number, or a proof combining Galois theory
In mathematics, Galois theory, originally introduced by Évariste Galois, provides a connection between field theory and group theory. This connection, the fundamental theorem of Galois theory, allows reducing certain problems in field theory t ...
and the fact that any real polynomial of ''odd'' degree has at least one real root.
Because of this fact, theorems that hold ''for any algebraically closed field'' apply to For example, any non-empty complex square matrix has at least one (complex) eigenvalue
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denot ...
.
Algebraic characterization
The field has the following three properties: * First, it has characteristic 0. This means that for any number of summands (all of which equal one). * Second, its transcendence degree over , the prime field of is thecardinality of the continuum
In set theory, the cardinality of the continuum is the cardinality or "size" of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by \mathfrak c (lowercase fraktur "c") or , \ma ...
.
* Third, it is algebraically closed (see above).
It can be shown that any field having these properties is isomorphic (as a field) to For example, the algebraic closure of the field of the -adic number also satisfies these three properties, so these two fields are isomorphic (as fields, but not as topological fields). Also, is isomorphic to the field of complex Puiseux series. However, specifying an isomorphism requires the axiom of choice
In mathematics, the axiom of choice, or AC, is an axiom of set theory equivalent to the statement that ''a Cartesian product of a collection of non-empty sets is non-empty''. Informally put, the axiom of choice says that given any collection ...
. Another consequence of this algebraic characterization is that contains many proper subfields that are isomorphic to .
Characterization as a topological field
The preceding characterization of describes only the algebraic aspects of That is to say, the properties of nearness and continuity, which matter in areas such asanalysis
Analysis ( : analyses) is the process of breaking a complex topic or substance into smaller parts in order to gain a better understanding of it. The technique has been applied in the study of mathematics and logic since before Aristotle (3 ...
and topology
In mathematics, topology (from the Greek words , and ) is concerned with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling, and bending; that is, without closing ho ...
, are not dealt with. The following description of as a topological field (that is, a field that is equipped with a topology
In mathematics, topology (from the Greek words , and ) is concerned with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling, and bending; that is, without closing ho ...
, which allows the notion of convergence) does take into account the topological properties. contains a subset (namely the set of positive real numbers) of nonzero elements satisfying the following three conditions:
* is closed under addition, multiplication and taking inverses.
* If and are distinct elements of , then either or is in .
* If is any nonempty subset of , then for some in
Moreover, has a nontrivial involutive automorphism (namely the complex conjugation), such that is in for any nonzero in
Any field with these properties can be endowed with a topology by taking the sets as a base, where ranges over the field and ranges over . With this topology is isomorphic as a ''topological'' field to
The only connected locally compact In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space. More precisely, it is a topological space in which e ...
topological fields are and This gives another characterization of as a topological field, since can be distinguished from because the nonzero complex numbers are connected, while the nonzero real numbers are not.
Formal construction
Construction as ordered pairs
William Rowan Hamilton
Sir William Rowan Hamilton LL.D, DCL, MRIA, FRAS (3/4 August 1805 – 2 September 1865) was an Irish mathematician, astronomer, and physicist. He was the Andrews Professor of Astronomy at Trinity College Dublin, and Royal Astronomer of Ire ...
introduced the approach to define the set of complex numbers as the set of of real numbers, in which the following rules for addition and multiplication are imposed:
It is then just a matter of notation to express as .
Construction as a quotient field
Though this low-level construction does accurately describe the structure of the complex numbers, the following equivalent definition reveals the algebraic nature of more immediately. This characterization relies on the notion of fields and polynomials. A field is a set endowed with addition, subtraction, multiplication and division operations that behave as is familiar from, say, rational numbers. For example, the distributive law must hold for any three elements , and of a field. The set of real numbers does form a field. A polynomial with realcoefficient
In mathematics, a coefficient is a multiplicative factor in some term of a polynomial, a series, or an expression; it is usually a number, but may be any expression (including variables such as , and ). When the coefficients are themselves ...
s is an expression of the form
where the are real numbers. The usual addition and multiplication of polynomials endows the set