|
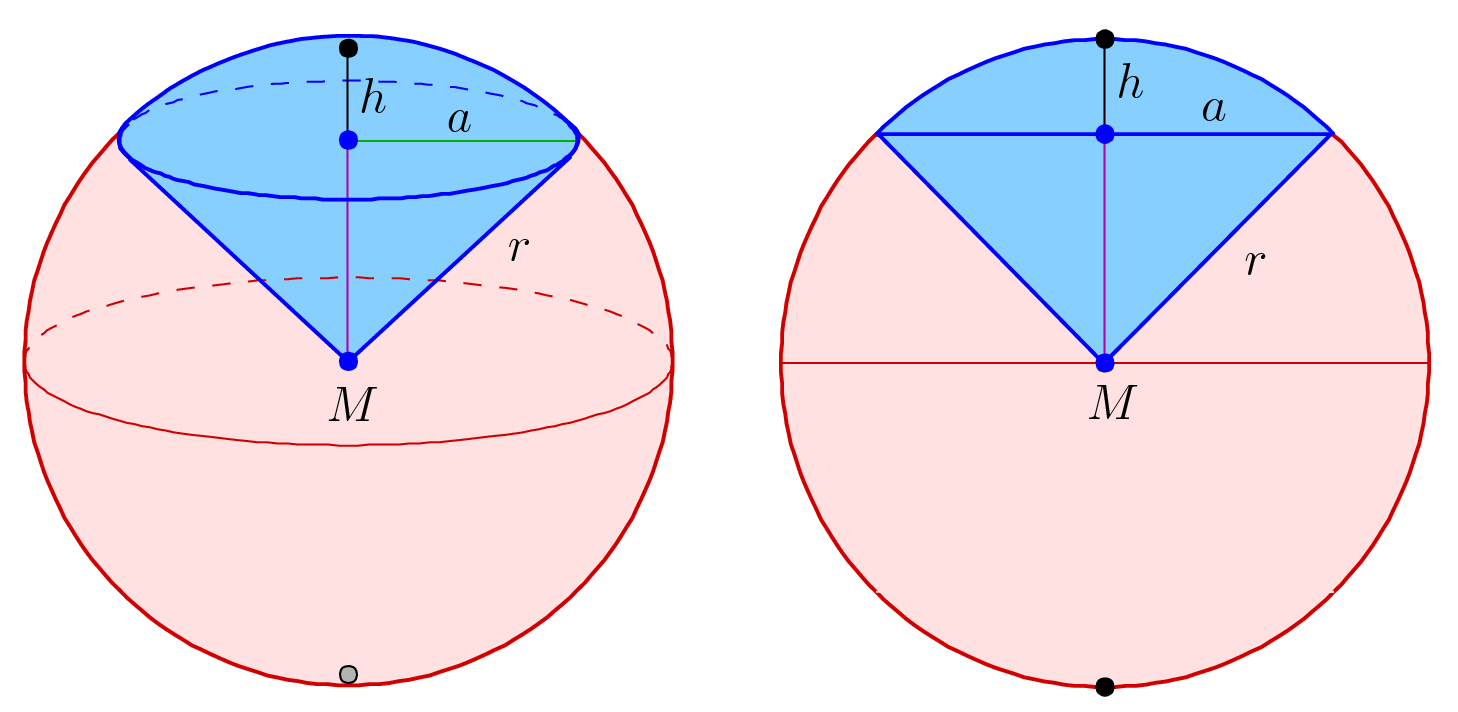
Spherical Cap
In geometry, a spherical cap or spherical dome is a portion of a sphere or of a ball cut off by a plane. It is also a spherical segment of one base, i.e., bounded by a single plane. If the plane passes through the center of the sphere (forming a great circle), so that the height of the cap is equal to the radius of the sphere, the spherical cap is called a ''hemisphere''. Volume and surface area The volume of the spherical cap and the area of the curved surface may be calculated using combinations of * The radius r of the sphere * The radius a of the base of the cap * The height h of the cap * The polar angle \theta between the rays from the center of the sphere to the apex of the cap (the pole) and the edge of the disk forming the base of the cap If \phi denotes the latitude in geographic coordinates, then \theta+\phi = \pi/2 = 90^\circ\,, and \cos \theta = \sin \phi. The relationship between h and r is relevant as long as 0\le h\le2r. For example, the red section of the illu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Cap Diagram
A sphere () is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. A sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the centre of the sphere, and is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians. The sphere is a fundamental object in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres roll smoothly in any direction, so most balls used in sports and toys are spherical, as are ball bearings. Basic terminology As mentioned earlier is the sphere's r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Sector
In geometry, a spherical sector, also known as a spherical cone, is a portion of a sphere or of a ball defined by a conical boundary with apex at the center of the sphere. It can be described as the union of a spherical cap and the cone formed by the center of the sphere and the base of the cap. It is the three-dimensional analogue of the sector of a circle. Volume If the radius of the sphere is denoted by ''r'' and the height of the cap by ''h'', the volume of the spherical sector is :V=\frac\,. This may also be written as :V=\frac(1-\cos\varphi)\,, where ''φ'' is half the cone angle, i.e., ''φ'' is the angle between the rim of the cap and the direction to the middle of the cap as seen from the sphere center. The volume ''V'' of the sector is related to the area ''A'' of the cap by: :V=\frac\,. Area The curved surface area of the spherical sector (on the surface of the sphere, excluding the cone surface) is :A=2\pi rh\,. It is also :A=\Omega r^2 where Ω is th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ellipsoid
An ellipsoid is a surface that may be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation. An ellipsoid is a quadric surface; that is, a surface that may be defined as the zero set of a polynomial of degree two in three variables. Among quadric surfaces, an ellipsoid is characterized by either of the two following properties. Every planar cross section is either an ellipse, or is empty, or is reduced to a single point (this explains the name, meaning "ellipse-like"). It is bounded, which means that it may be enclosed in a sufficiently large sphere. An ellipsoid has three pairwise perpendicular axes of symmetry which intersect at a center of symmetry, called the center of the ellipsoid. The line segments that are delimited on the axes of symmetry by the ellipsoid are called the ''principal axes'', or simply axes of the ellipsoid. If the three axes have different lengths, the figure is a triaxial ellipsoid (r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ellipsoidal Dome
An ellipsoidal dome is a dome (also see geodesic dome), which has a bottom cross-section which is a circle, but has a cupola whose curve is an ellipse. There are two types of ellipsoidal domes: ''prolate ellipsoidal domes'' and ''oblate ellipsoidal domes''. A prolate ellipsoidal dome is derived by rotating an ellipse around the long axis of the ellipse; an oblate ellipsoidal dome is derived by rotating an ellipse around the short axis of the ellipse. Of small note, in reflecting telescopes the mirror is usually elliptical, so has the form of a "hollow" ellipsoidal dome. The Jameh Mosque of Yazd has an ellipsoidal dome. See also * Beehive tomb * Clochán * Cloister vault * Dome * Ellipsoid * Ellipsoidal coordinates * Elliptical dome * Geodesic dome * Geodesics on an ellipsoid * Great ellipse * Onion dome * Spherical cap * Spheroid A spheroid, also known as an ellipsoid of revolution or rotational ellipsoid, is a quadric surface obtained by rotating an ellipse abou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circular Symmetry
In geometry, circular symmetry is a type of continuous symmetry for a planar object that can be rotated by any arbitrary angle and map onto itself. Rotational circular symmetry is isomorphic with the circle group in the complex plane, or the special orthogonal group SO(2), and unitary group U(1). Reflective circular symmetry is isomorphic with the orthogonal group O(2). Two dimensions A 2-dimensional object with circular symmetry would consist of concentric circles and annular domains. Rotational circular symmetry has all cyclic symmetry, Z''n'' as subgroup symmetries. Reflective circular symmetry has all dihedral symmetry, Dih''n'' as subgroup symmetries. Three dimensions In 3-dimensions, a surface or solid of revolution has circular symmetry around an axis, also called cylindrical symmetry or axial symmetry. An example is a right circular cone. Circular symmetry in 3 dimensions has all pyramidal symmetry, C''n''v as subgroups. A double-cone, bicone, cylinder, toro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spheroid
A spheroid, also known as an ellipsoid of revolution or rotational ellipsoid, is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters. A spheroid has circular symmetry. If the ellipse is rotated about its major axis, the result is a ''prolate spheroid'', elongated like a rugby ball. The American football is similar but has a pointier end than a spheroid could. If the ellipse is rotated about its minor axis, the result is an ''oblate spheroid'', flattened like a lentil or a plain M&M. If the generating ellipse is a circle, the result is a sphere. Due to the combined effects of gravity and rotation, the figure of the Earth (and of all planets) is not quite a sphere, but instead is slightly flattened in the direction of its axis of rotation. For that reason, in cartography and geodesy the Earth is often approximated by an oblate spheroid, known as the reference ellipsoid, instead of a sph ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tropics
The tropics are the regions of Earth surrounding the Equator. They are defined in latitude by the Tropic of Cancer in the Northern Hemisphere at N and the Tropic of Capricorn in the Southern Hemisphere at S. The tropics are also referred to as the tropical zone and the torrid zone (see geographical zone). In terms of climate, the tropics receive sunlight that is more direct than the rest of Earth and are generally hotter and wetter as they aren't affected as much by the solar seasons. The word "tropical" sometimes refers to this sort of climate in the zone rather than to the geographical zone itself. The tropical zone includes deserts and snow-capped mountains, which are not tropical in the climatic sense. The tropics are distinguished from the other climatic and biomatic regions of Earth, which are the middle latitudes and the polar regions on either side of the equatorial zone. The tropics constitute 40% of Earth's surface area and contain 36% of Earth's landmass. , the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Union (set Theory)
In set theory, the union (denoted by ∪) of a collection of sets is the set of all elements in the collection. It is one of the fundamental operations through which sets can be combined and related to each other. A refers to a union of zero (0) sets and it is by definition equal to the empty set. For explanation of the symbols used in this article, refer to the table of mathematical symbols. Union of two sets The union of two sets ''A'' and ''B'' is the set of elements which are in ''A'', in ''B'', or in both ''A'' and ''B''. In set-builder notation, :A \cup B = \. For example, if ''A'' = and ''B'' = then ''A'' ∪ ''B'' = . A more elaborate example (involving two infinite sets) is: : ''A'' = : ''B'' = : A \cup B = \ As another example, the number 9 is ''not'' contained in the union of the set of prime numbers and the set of even numbers , because 9 is neither prime nor even. Sets cannot have duplicate elements, so the union of the sets and is . Multip ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solid Of Revolution
In geometry, a solid of revolution is a solid figure obtained by rotating a plane figure around some straight line (the ''axis of revolution'') that lies on the same plane. The surface created by this revolution and which bounds the solid is the surface of revolution. Assuming that the curve does not cross the axis, the solid's volume is equal to the length of the circle described by the figure's centroid multiplied by the figure's area ( Pappus's second centroid theorem). A representative disc is a three-dimensional volume element of a solid of revolution. The element is created by rotating a line segment (of length ) around some axis (located units away), so that a cylindrical volume of units is enclosed. Finding the volume Two common methods for finding the volume of a solid of revolution are the disc method and the shell method of integration. To apply these methods, it is easiest to draw the graph in question; identify the area that is to be revolved about the axis o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Of Revolution
A surface of revolution is a surface in Euclidean space created by rotating a curve (the generatrix) around an axis of rotation. Examples of surfaces of revolution generated by a straight line are cylindrical and conical surfaces depending on whether or not the line is parallel to the axis. A circle that is rotated around any diameter generates a sphere of which it is then a great circle, and if the circle is rotated around an axis that does not intersect the interior of a circle, then it generates a torus which does not intersect itself (a ring torus). Properties The sections of the surface of revolution made by planes through the axis are called ''meridional sections''. Any meridional section can be considered to be the generatrix in the plane determined by it and the axis. The sections of the surface of revolution made by planes that are perpendicular to the axis are circles. Some special cases of hyperboloids (of either one or two sheets) and elliptic paraboloids are su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Cap From Rotation
A sphere () is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. A sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the centre of the sphere, and is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians. The sphere is a fundamental object in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres roll smoothly in any direction, so most balls used in sports and toys are spherical, as are ball bearings. Basic terminology As mentioned earlier is the sphere's r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Area
Area is the quantity that expresses the extent of a region on the plane or on a curved surface. The area of a plane region or ''plane area'' refers to the area of a shape A shape or figure is a graphics, graphical representation of an object or its external boundary, outline, or external Surface (mathematics), surface, as opposed to other properties such as color, Surface texture, texture, or material type. A pl ... or planar lamina, while ''surface area'' refers to the area of an open surface or the boundary (mathematics), boundary of a solid geometry, three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analogue of the length of a plane curve, curve (a one-dimensional concept) or the volume of a solid (a three-dimensional concept). The area of a shape can be measured by com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |