|
Recursive Filter
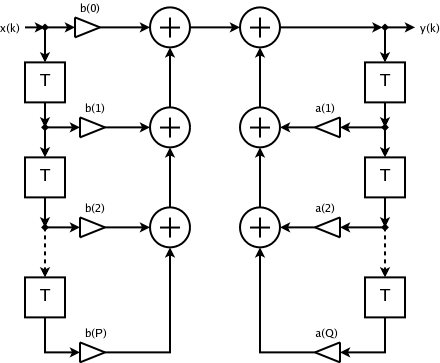
In signal processing, a recursive filter is a type of filter which reuses one or more of its outputs as an input. This feedback typically results in an unending impulse response (commonly referred to as ''infinite impulse response'' (IIR)), characterised by either exponentially growing, decaying, or sinusoidal signal output components. However, a recursive filter does not always have an infinite impulse response. Some implementations of moving average filter are recursive filters but with a finite impulse response. Non-recursive Filter Example: y = 0.5x − 1+ 0.5x Recursive Filter Example: y = 0.5y − 1+ 0.5x Examples of recursive filters *Kalman filter In statistics and control theory, Kalman filtering (also known as linear quadratic estimation) is an algorithm that uses a series of measurements observed over time, including statistical noise and other inaccuracies, to produce estimates of unk ... Signal processing {{signal-processing-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Signal Processing
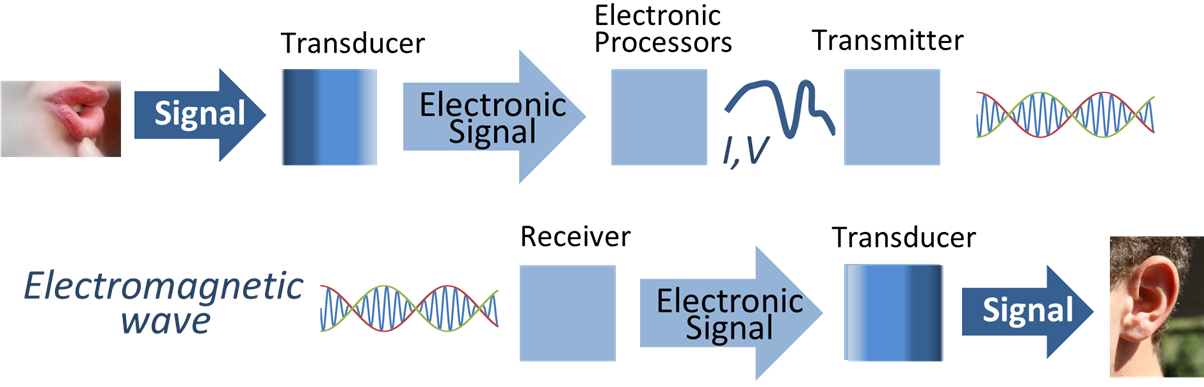
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, Scalar potential, potential fields, Seismic tomography, seismic signals, Altimeter, altimetry processing, and scientific measurements. Signal processing techniques are used to optimize transmissions, Data storage, digital storage efficiency, correcting distorted signals, improve subjective video quality, and to detect or pinpoint components of interest in a measured signal. History According to Alan V. Oppenheim and Ronald W. Schafer, the principles of signal processing can be found in the classical numerical analysis techniques of the 17th century. They further state that the digital refinement of these techniques can be found in the digital control systems of the 1940s and 1950s. In 1948, Claude Shannon wrote the influential paper "A Mathematical Theory of Communication" which was publis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Filter (signal Processing)
In signal processing, a filter is a device or process that removes some unwanted components or features from a Signal (electronics), signal. Filtering is a class of signal processing, the defining feature of filters being the complete or partial suppression of some aspect of the signal. Most often, this means removing some frequency, frequencies or frequency bands. However, filters do not exclusively act in the frequency domain; especially in the field of image processing many other targets for filtering exist. Correlations can be removed for certain frequency components and not for others without having to act in the frequency domain. Filters are widely used in electronics and telecommunication, in radio, television, audio recording, radar, control systems, music synthesis, image processing, computer graphics, and structural dynamics. There are many different bases of classifying filters and these overlap in many different ways; there is no simple hierarchical classification. Fil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Feedback
Feedback occurs when outputs of a system are routed back as inputs as part of a chain of cause and effect that forms a circuit or loop. The system can then be said to ''feed back'' into itself. The notion of cause-and-effect has to be handled carefully when applied to feedback systems: History Self-regulating mechanisms have existed since antiquity, and the idea of feedback started to enter economic theory in Britain by the 18th century, but it was not at that time recognized as a universal abstraction and so did not have a name. The first ever known artificial feedback device was a float valve, for maintaining water at a constant level, invented in 270 BC in Alexandria, Egypt. This device illustrated the principle of feedback: a low water level opens the valve, the rising water then provides feedback into the system, closing the valve when the required level is reached. This then reoccurs in a circular fashion as the water level fluctuates. Centrifugal governors were ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Impulse Response
In signal processing and control theory, the impulse response, or impulse response function (IRF), of a dynamic system is its output when presented with a brief input signal, called an impulse (). More generally, an impulse response is the reaction of any dynamic system in response to some external change. In both cases, the impulse response describes the reaction of the system as a function of time (or possibly as a function of some other independent variable that parameterizes the dynamic behavior of the system). In all these cases, the dynamic system and its impulse response may be actual physical objects, or may be mathematical systems of equations describing such objects. Since the impulse function contains all frequencies (see the Fourier transform of the Dirac delta function, showing infinite frequency bandwidth that the Dirac delta function has), the impulse response defines the response of a linear time-invariant system for all frequencies. Mathematical considerat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Infinite Impulse Response
Infinite impulse response (IIR) is a property applying to many linear time-invariant systems that are distinguished by having an impulse response h(t) that does not become exactly zero past a certain point but continues indefinitely. This is in contrast to a finite impulse response (FIR) system, in which the impulse response ''does'' become exactly zero at times t>T for some finite T, thus being of finite duration. Common examples of linear time-invariant systems are most electronic and digital filters. Systems with this property are known as ''IIR systems'' or ''IIR filters''. In practice, the impulse response, even of IIR systems, usually approaches zero and can be neglected past a certain point. However the physical systems which give rise to IIR or FIR responses are dissimilar, and therein lies the importance of the distinction. For instance, analog electronic filters composed of resistors, capacitors, and/or inductors (and perhaps linear amplifiers) are generally IIR filte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Exponential Growth
Exponential growth occurs when a quantity grows as an exponential function of time. The quantity grows at a rate directly proportional to its present size. For example, when it is 3 times as big as it is now, it will be growing 3 times as fast as it is now. In more technical language, its instantaneous rate of change (that is, the derivative) of a quantity with respect to an independent variable is proportional to the quantity itself. Often the independent variable is time. Described as a function, a quantity undergoing exponential growth is an exponential function of time, that is, the variable representing time is the exponent (in contrast to other types of growth, such as quadratic growth). Exponential growth is the inverse of logarithmic growth. Not all cases of growth at an always increasing rate are instances of exponential growth. For example the function f(x) = x^3 grows at an ever increasing rate, but is much slower than growing exponentially. For example, w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Exponential Decay
A quantity is subject to exponential decay if it decreases at a rate proportional to its current value. Symbolically, this process can be expressed by the following differential equation, where is the quantity and (lambda Lambda (; uppercase , lowercase ; , ''lám(b)da'') is the eleventh letter of the Greek alphabet, representing the voiced alveolar lateral approximant . In the system of Greek numerals, lambda has a value of 30. Lambda is derived from the Phoen ...) is a positive rate called the exponential decay constant, disintegration constant, rate constant, or transformation constant: :\frac = -\lambda N(t). The solution to this equation (see #Solution_of_the_differential_equation, derivation below) is: :N(t) = N_0 e^, where is the quantity at time , is the initial quantity, that is, the quantity at time . Measuring rates of decay Mean lifetime If the decaying quantity, ''N''(''t''), is the number of discrete elements in a certain set (mathematics), se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Sine Wave
A sine wave, sinusoidal wave, or sinusoid (symbol: ∿) is a periodic function, periodic wave whose waveform (shape) is the trigonometric function, trigonometric sine, sine function. In mechanics, as a linear motion over time, this is ''simple harmonic motion''; as rotation, it corresponds to ''uniform circular motion''. Sine waves occur often in physics, including wind waves, sound waves, and light waves, such as monochromatic radiation. In engineering, signal processing, and mathematics, Fourier analysis decomposes general functions into a sum of sine waves of various frequencies, relative phases, and magnitudes. When any two sine waves of the same frequency (but arbitrary phase (waves), phase) are linear combination, linearly combined, the result is another sine wave of the same frequency; this property is unique among periodic waves. Conversely, if some phase is chosen as a zero reference, a sine wave of arbitrary phase can be written as the linear combination of two sine wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |