|
Motor Variable
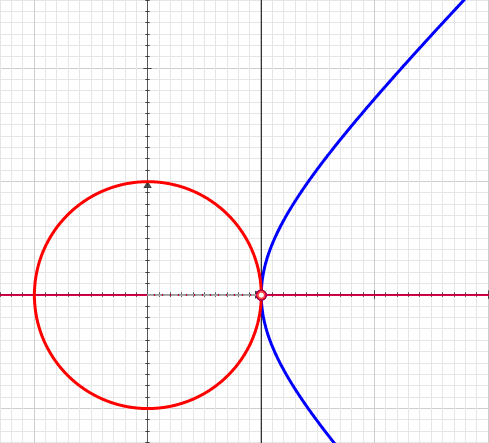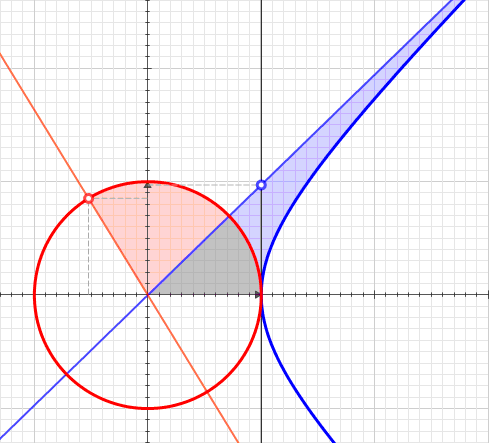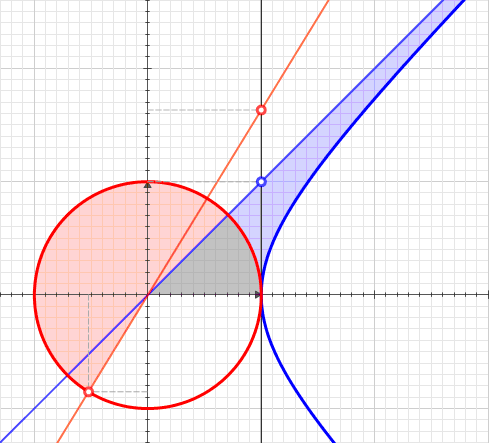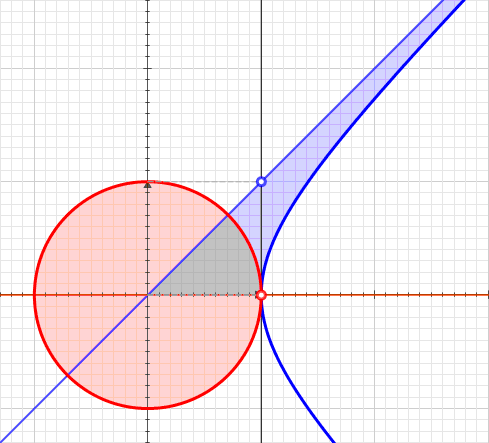
In mathematics, a function of a motor variable is a function with arguments and values in the split-complex number plane, much as functions of a complex variable involve ordinary complex numbers. William Kingdon Clifford coined the term motor for a kinematic operator in his "Preliminary Sketch of Biquaternions" (1873). He used split-complex numbers for scalars in his split-biquaternions. ''Motor variable'' is used here in place of ''split-complex variable'' for euphony and tradition. For example, :f(z) = u(z) + j \ v(z) ,\ z = x + j y ,\ x,y \in R ,\quad j^2 = +1,\quad u(z),v(z) \in R. Functions of a motor variable provide a context to extend real analysis and provide compact representation of mappings of the plane. However, the theory falls well short of function theory on the ordinary complex plane. Nevertheless, some of the aspects of conventional complex analysis have an interpretation given with motor variables, and more generally in hypercomplex analysis. Elementary funct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projective Line Over A Ring
In mathematics, the projective line over a ring is an extension of the concept of projective line over a field. Given a ring ''A'' with 1, the projective line P(''A'') over ''A'' consists of points identified by projective coordinates. Let ''U'' be the group of units of ''A''; pairs (''a, b'') and (''c, d'') from are related when there is a ''u'' in ''U'' such that and . This relation is an equivalence relation. A typical equivalence class is written ''U'' 'a, b'' that is, ''U'' 'a, b''is in the projective line if the ideal generated by ''a'' and ''b'' is all of ''A''. The projective line P(''A'') is equipped with a group of homographies. The homographies are expressed through use of the matrix ring over ''A'' and its group of units ''V'' as follows: If ''c'' is in Z(''U''), the center of ''U'', then the group action of matrix \beginc & 0 \\ 0 & c \end on P(''A'') is the same as the action of the identity matrix. Such matrices represent a normal subgroup ''N'' of ''V''. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Range Of A Function
In mathematics, the range of a function may refer to either of two closely related concepts: * The codomain of the function * The image of the function Given two sets and , a binary relation between and is a (total) function (from to ) if for every in there is exactly one in such that relates to . The sets and are called domain and codomain of , respectively. The image of is then the subset of consisting of only those elements of such that there is at least one in with . Terminology As the term "range" can have different meanings, it is considered a good practice to define it the first time it is used in a textbook or article. Older books, when they use the word "range", tend to use it to mean what is now called the codomain. More modern books, if they use the word "range" at all, generally use it to mean what is now called the image. To avoid any confusion, a number of modern books don't use the word "range" at all. Elaboration and example Given a funct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Connected Component (topology)
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint non-empty open subsets. Connectedness is one of the principal topological properties that are used to distinguish topological spaces. A subset of a topological space X is a if it is a connected space when viewed as a subspace of X. Some related but stronger conditions are path connected, simply connected, and n-connected. Another related notion is '' locally connected'', which neither implies nor follows from connectedness. Formal definition A topological space X is said to be if it is the union of two disjoint non-empty open sets. Otherwise, X is said to be connected. A subset of a topological space is said to be connected if it is connected under its subspace topology. Some authors exclude the empty set (with its unique topology) as a connected space, but this article does not follow that practice. For a topologi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Function
The exponential function is a mathematical function denoted by f(x)=\exp(x) or e^x (where the argument is written as an exponent). Unless otherwise specified, the term generally refers to the positive-valued function of a real variable, although it can be extended to the complex numbers or generalized to other mathematical objects like matrices or Lie algebras. The exponential function originated from the notion of exponentiation (repeated multiplication), but modern definitions (there are several equivalent characterizations) allow it to be rigorously extended to all real arguments, including irrational numbers. Its ubiquitous occurrence in pure and applied mathematics led mathematician Walter Rudin to opine that the exponential function is "the most important function in mathematics". The exponential function satisfies the exponentiation identity e^ = e^x e^y \text x,y\in\mathbb, which, along with the definition e = \exp(1), shows that e^n=\underbrace_ for positi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compactification
{{disambiguation ...
Compactification may refer to: * Compactification (mathematics), making a topological space compact * Compactification (physics), the "curling up" of extra dimensions in string theory See also * Compaction (other) Compaction may refer to: * Soil compaction, for mechanically induced compaction near the ground surface * Compaction of ceramic powders * Compaction (geology), part of the process of lithification involving mechanical dewatering of a sediment by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bijection
In mathematics, a bijection, also known as a bijective function, one-to-one correspondence, or invertible function, is a function between the elements of two sets, where each element of one set is paired with exactly one element of the other set, and each element of the other set is paired with exactly one element of the first set. There are no unpaired elements. In mathematical terms, a bijective function is a one-to-one (injective) and onto (surjective) mapping of a set ''X'' to a set ''Y''. The term ''one-to-one correspondence'' must not be confused with ''one-to-one function'' (an injective function; see figures). A bijection from the set ''X'' to the set ''Y'' has an inverse function from ''Y'' to ''X''. If ''X'' and ''Y'' are finite sets, then the existence of a bijection means they have the same number of elements. For infinite sets, the picture is more complicated, leading to the concept of cardinal number—a way to distinguish the various sizes of infinite se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rectangle
In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal (360°/4 = 90°); or a parallelogram containing a right angle. A rectangle with four sides of equal length is a '' square''. The term " oblong" is occasionally used to refer to a non- square rectangle. A rectangle with vertices ''ABCD'' would be denoted as . The word rectangle comes from the Latin ''rectangulus'', which is a combination of ''rectus'' (as an adjective, right, proper) and ''angulus'' (angle). A crossed rectangle is a crossed (self-intersecting) quadrilateral which consists of two opposite sides of a rectangle along with the two diagonals (therefore only two sides are parallel). It is a special case of an antiparallelogram, and its angles are not right angles and not all equal, though opposite angles are equal. Other geometries, such as spherical, elliptic, and hy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Disk
In mathematics, the open unit disk (or disc) around ''P'' (where ''P'' is a given point in the plane), is the set of points whose distance from ''P'' is less than 1: :D_1(P) = \.\, The closed unit disk around ''P'' is the set of points whose distance from ''P'' is less than or equal to one: :\bar D_1(P)=\.\, Unit disks are special cases of disks and unit balls; as such, they contain the interior of the unit circle and, in the case of the closed unit disk, the unit circle itself. Without further specifications, the term ''unit disk'' is used for the open unit disk about the origin, D_1(0), with respect to the standard Euclidean metric. It is the interior of a circle of radius 1, centered at the origin. This set can be identified with the set of all complex numbers of absolute value less than one. When viewed as a subset of the complex plane (C), the unit disk is often denoted \mathbb. The open unit disk, the plane, and the upper half-plane The function :f(z)=\frac is an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cayley Transform
In mathematics, the Cayley transform, named after Arthur Cayley, is any of a cluster of related things. As originally described by , the Cayley transform is a mapping between skew-symmetric matrices and special orthogonal matrices. The transform is a homography used in real analysis, complex analysis, and quaternionic analysis. In the theory of Hilbert spaces, the Cayley transform is a mapping between linear operators . Real homography The Cayley transform is an automorphism of the real projective line that permutes the elements of in sequence. For example, it maps the positive real numbers to the interval ��1, 1 Thus the Cayley transform is used to adapt Legendre polynomials for use with functions on the positive real numbers with Legendre rational functions. As a real homography, points are described with projective coordinates, and the mapping is : ,\ 1= \left frac ,\ 1\right\thicksim - 1, \ x + 1= ,\ 1begin1 & 1 \\ -1 & 1 \end . Complex homography On the Riemann ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conformal Map
In mathematics, a conformal map is a function that locally preserves angles, but not necessarily lengths. More formally, let U and V be open subsets of \mathbb^n. A function f:U\to V is called conformal (or angle-preserving) at a point u_0\in U if it preserves angles between directed curves through u_0, as well as preserving orientation. Conformal maps preserve both angles and the shapes of infinitesimally small figures, but not necessarily their size or curvature. The conformal property may be described in terms of the Jacobian derivative matrix of a coordinate transformation. The transformation is conformal whenever the Jacobian at each point is a positive scalar times a rotation matrix (orthogonal with determinant one). Some authors define conformality to include orientation-reversing mappings whose Jacobians can be written as any scalar times any orthogonal matrix. For mappings in two dimensions, the (orientation-preserving) conformal mappings are precisely the locally ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Angle
In geometry, hyperbolic angle is a real number determined by the area of the corresponding hyperbolic sector of ''xy'' = 1 in Quadrant I of the Cartesian plane. The hyperbolic angle parametrises the unit hyperbola, which has hyperbolic functions as coordinates. In mathematics, hyperbolic angle is an invariant measure as it is preserved under hyperbolic rotation. The hyperbola ''xy'' = 1 is rectangular with a semi-major axis of \sqrt 2, analogous to the magnitude of a circular angle corresponding to the area of a circular sector in a circle with radius \sqrt 2. Hyperbolic angle is used as the independent variable for the hyperbolic functions sinh, cosh, and tanh, because these functions may be premised on hyperbolic analogies to the corresponding circular trigonometric functions by regarding a hyperbolic angle as defining a hyperbolic triangle. The parameter thus becomes one of the most useful in the calculus of real variables. Definition Consider the rectangular hyperbola ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |