|
Multi-configuration Time-dependent Hartree
Multi-configuration time-dependent Hartree (MCTDH) is a general algorithm to solve the time-dependent Schrödinger equation for multidimensional dynamical systems consisting of distinguishable particles. MCTDH can thus determine the quantal motion of the nuclei of a molecular system evolving on one or several coupled electronic potential energy surfaces. MCTDH by its very nature is an approximate method. However, it can be made as accurate as any competing method, but its numerical efficiency deteriorates with growing accuracy. MCTDH is designed for multi-dimensional problems, in particular for problems that are difficult or even impossible to attack in a conventional way. There is no or only little gain when treating systems with less than three degrees of freedom In many scientific fields, the degrees of freedom of a system is the number of parameters of the system that may vary independently. For example, a point in the plane has two degrees of freedom for translation: its ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Douglas Hartree
Douglas Rayner Hartree (27 March 1897 – 12 February 1958) was an English mathematician and physicist most famous for the development of numerical analysis and its application to the Hartree–Fock equations of atomic physics and the construction of a differential analyser using Meccano. Early life and education Douglas Hartree was born in Cambridge, England. His father, William, was a lecturer in engineering at the University of Cambridge. His mother, Eva Rayner, was president of the National Council of Women of Great Britain and first woman to be mayor of the city of Cambridge. One of his great-grandfathers was Samuel Smiles; another was the marine engineer William Hartree, partner of John Penn. Douglas Hartree was the oldest of three sons who survived infancy. A brother and sister died in infancy when he was still a child, but his two brothers would later also die. Hartree's 7-year-old brother John Edwin died when Hartree was 17, and Hartree's 22-year-old broth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Schrödinger Equation
The Schrödinger equation is a partial differential equation that governs the wave function of a non-relativistic quantum-mechanical system. Its discovery was a significant landmark in the development of quantum mechanics. It is named after Erwin Schrödinger, an Austrian physicist, who postulated the equation in 1925 and published it in 1926, forming the basis for the work that resulted in his Nobel Prize in Physics in 1933. Conceptually, the Schrödinger equation is the quantum counterpart of Newton's second law in classical mechanics. Given a set of known initial conditions, Newton's second law makes a mathematical prediction as to what path a given physical system will take over time. The Schrödinger equation gives the evolution over time of the wave function, the quantum-mechanical characterization of an isolated physical system. The equation was postulated by Schrödinger based on a postulate of Louis de Broglie that all matter has an associated matter wave. The equati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Elementary Particle
In particle physics, an elementary particle or fundamental particle is a subatomic particle that is not composed of other particles. The Standard Model presently recognizes seventeen distinct particles—twelve fermions and five bosons. As a consequence of flavor and color combinations and antimatter, the fermions and bosons are known to have 48 and 13 variations, respectively. Among the 61 elementary particles embraced by the Standard Model number: electrons and other leptons, quarks, and the fundamental bosons. Subatomic particles such as protons or neutrons, which contain two or more elementary particles, are known as composite particles. Ordinary matter is composed of atoms, themselves once thought to be indivisible elementary particles. The name ''atom'' comes from the Ancient Greek word ''ἄτομος'' ( atomos) which means ''indivisible'' or ''uncuttable''. Despite the theories about atoms that had existed for thousands of years, the factual existence of ato ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Molecule
A molecule is a group of two or more atoms that are held together by Force, attractive forces known as chemical bonds; depending on context, the term may or may not include ions that satisfy this criterion. In quantum physics, organic chemistry, and biochemistry, the distinction from ions is dropped and ''molecule'' is often used when referring to polyatomic ions. A molecule may be homonuclear, that is, it consists of atoms of one chemical element, e.g. two atoms in the oxygen molecule (O2); or it may be heteronuclear, a chemical compound composed of more than one element, e.g. water (molecule), water (two hydrogen atoms and one oxygen atom; H2O). In the kinetic theory of gases, the term ''molecule'' is often used for any gaseous particle regardless of its composition. This relaxes the requirement that a molecule contains two or more atoms, since the noble gases are individual atoms. Atoms and complexes connected by non-covalent interactions, such as hydrogen bonds or ionic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Vibronic Coupling
Vibronic coupling (also called nonadiabatic coupling or derivative coupling) in a molecule involves the interaction between electronic and nuclear vibrational motion. The term "vibronic" originates from the combination of the terms "vibrational" and "electronic", denoting the idea that in a molecule, vibrational and electronic interactions are interrelated and influence each other. The magnitude of vibronic coupling reflects the degree of such interrelation. In theoretical chemistry, the vibronic coupling is neglected within the Born–Oppenheimer approximation. Vibronic couplings are crucial to the understanding of nonadiabatic processes, especially near points of conical intersections. The direct calculation of vibronic couplings used to be uncommon due to difficulties associated with its evaluation, but has recently gained popularity due to increased interest in the quantitative prediction of internal conversion rates, as well as the development of cheap but rigorous ways ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
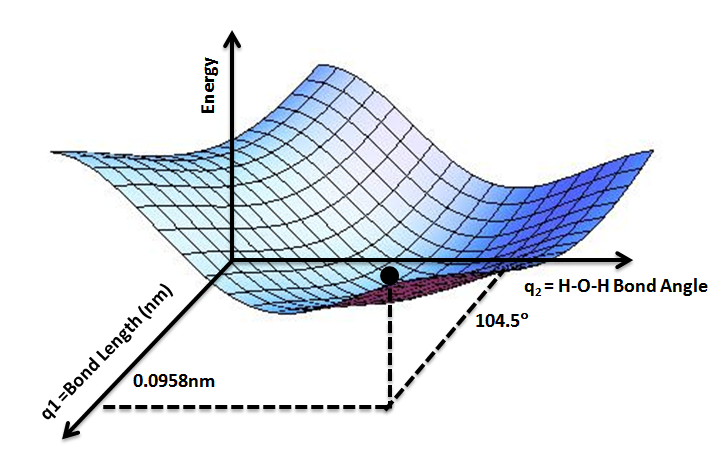
Potential Energy Surface
A potential energy surface (PES) or energy landscape describes the energy of a Physical system, system, especially a collection of atoms, in terms of certain Parameter, parameters, normally the positions of the atoms. The Surface (mathematics), surface might define the energy as a Function (mathematics), function of one or more coordinates; if there is only one coordinate, the surface is called a ''potential energy curve'' or energy profile. An example is the Morse/Long-range potential. It is helpful to use the analogy of a landscape: for a system with two Degrees of freedom (physics and chemistry), degrees of freedom (e.g. two bond lengths), the value of the energy (analogy: the height of the land) is a function of two bond lengths (analogy: the coordinates of the position on the ground). The PES concept finds application in fields such as physics, chemistry and biochemistry, especially in the theoretical sub-branches of these subjects. It can be used to theoretically explore p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Degrees Of Freedom (physics And Chemistry)
In physics and chemistry, a degree of freedom is an independent physical parameter in the chosen parameterization of a physical system. More formally, given a parameterization of a physical system, the number of degrees of freedom is the smallest number n of parameters whose values need to be known in order to always be possible to determine the values of ''all'' parameters in the chosen parameterization. In this case, any set of n such parameters are called degrees of freedom. The location of a particle in three-dimensional space requires three Coordinate system, position coordinates. Similarly, the direction and speed at which a particle moves can be described in terms of three velocity components, each in reference to the three dimensions of space. So, if the time evolution of the system is Deterministic system, deterministic (where the state at one instant uniquely determines its past and future position and velocity as a function of time), such a system has six degrees of f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Density Operator
In quantum mechanics, a density matrix (or density operator) is a matrix used in calculating the probabilities of the outcomes of measurements performed on physical systems. It is a generalization of the state vectors or wavefunctions: while those can only represent pure states, density matrices can also represent mixed states. These arise in quantum mechanics in two different situations: # when the preparation of a system can randomly produce different pure states, and thus one must deal with the statistics of possible preparations, and # when one wants to describe a physical system that is entangled with another, without describing their combined state. This case is typical for a system interacting with some environment (e.g. decoherence). In this case, the density matrix of an entangled system differs from that of an ensemble of pure states that, combined, would give the same statistical results upon measurement. Density matrices are thus crucial tools in areas of quantum me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Quantum Chemistry
Quantum chemistry, also called molecular quantum mechanics, is a branch of physical chemistry focused on the application of quantum mechanics to chemical systems, particularly towards the quantum-mechanical calculation of electronic contributions to physical and chemical properties of Molecule, molecules, Material, materials, and solutions at the atomic level. These calculations include systematically applied approximations intended to make calculations computationally feasible while still capturing as much information about important contributions to the computed Wave function, wave functions as well as to observable properties such as structures, spectra, and Thermodynamics, thermodynamic properties. Quantum chemistry is also concerned with the computation of quantum effects on molecular dynamics and chemical kinetics. Chemists rely heavily on spectroscopy through which information regarding the Quantization (physics), quantization of energy on a molecular scale can be obtained ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |