|
Gravitational Perturbation
In astronomy, perturbation is the complex motion of a massive body subjected to forces other than the gravitational attraction of a single other massive body. The other forces can include a third (fourth, fifth, etc.) body, resistance, as from an atmosphere, and the off-center attraction of an oblate or otherwise misshapen body. Introduction The study of perturbations began with the first attempts to predict planetary motions in the sky. In ancient times the causes were unknown. Isaac Newton, at the time he formulated his laws of motion and of gravitation, applied them to the first analysis of perturbations, recognizing the complex difficulties of their calculation. Many of the great mathematicians since then have given attention to the various problems involved; throughout the 18th and 19th centuries there was demand for accurate tables of the position of the Moon and planets for marine navigation. The complex motions of gravitational perturbations can be broken down. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Moon Perturbation Diagram
The Moon is Earth's only natural satellite. It Orbit of the Moon, orbits around Earth at Lunar distance, an average distance of (; about 30 times Earth diameter, Earth's diameter). The Moon rotation, rotates, with a rotation period (lunar day) that is synchronized to its orbital period (Lunar month#Synodic month, lunar month) of 29.5 Earth days. This is the product of Earth's gravitation having tidal forces, tidally pulled on the Moon until one part of it stopped rotating away from the near side of the Moon, near side, making always the same lunar surface face Earth. Conversley, the gravitational pull of the Moon, on Earth, is the main driver of Earth's tides. In geophysical definition of planet, geophysical terms, the Moon is a planetary-mass object or satellite planet. Its mass is 1.2% that of the Earth, and its diameter is , roughly one-quarter of Earth's (about as wide as the contiguous United States). Within the Solar System, it is the List of Solar System objects by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Conic Section
A conic section, conic or a quadratic curve is a curve obtained from a cone's surface intersecting a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though it was sometimes considered a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a '' focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the ''eccentricity''. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2; that is, as the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Celestial Mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of objects in outer space. Historically, celestial mechanics applies principles of physics (classical mechanics) to astronomical objects, such as stars and planets, to produce ephemeris data. History Modern analytic celestial mechanics started with Isaac Newton's ''Principia'' (1687). The name celestial mechanics is more recent than that. Newton wrote that the field should be called "rational mechanics". The term "dynamics" came in a little later with Gottfried Leibniz, and over a century after Newton, Pierre-Simon Laplace introduced the term ''celestial mechanics''. Prior to Kepler, there was little connection between exact, quantitative prediction of planetary positions, using geometrical or numerical techniques, and contemporary discussions of the physical causes of the planets' motion. Laws of planetary motion Johannes Kepler was the first to closely integrate the predictive geometrical a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Osculating Orbit
In astronomy, and in particular in astrodynamics, the osculating orbit of an object in space at a given moment in time is the gravitational Kepler orbit (i.e. an elliptic or other conic one) that it would have around its central body if perturbations were absent. That is, it is the orbit that coincides with the current orbital state vectors (position and velocity). Etymology The word '' osculate'' is Latin for "kiss". In mathematics, two curves osculate when they just touch, without (necessarily) crossing, at a point, where both have the same position and slope, i.e. the two curves "kiss". Kepler elements An osculating orbit and the object's position upon it can be fully described by the six standard Kepler orbital elements (osculating elements), which are easy to calculate as long as one knows the object's position and velocity relative to the central body. The osculating elements would remain constant in the absence of perturbations. Real astronomical orbits experience pe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Variation Of Parameters
In mathematics, variation of parameters, also known as variation of constants, is a general method to solve inhomogeneous differential equation, inhomogeneous linear ordinary differential equations. For first-order inhomogeneous linear differential equations it is usually possible to find solutions via integrating factors or method of undetermined coefficients, undetermined coefficients with considerably less effort, although those methods leverage heuristics that involve guessing and do not work for all inhomogeneous linear differential equations. Variation of parameters extends to linear partial differential equations as well, specifically to inhomogeneous problems for linear evolution equations like the heat equation, wave equation, and vibrating plate equation. In this setting, the method is more often known as Duhamel's principle, named after Jean-Marie Duhamel (1797–1872) who first applied the method to solve the inhomogeneous heat equation. Sometimes variation of parame ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
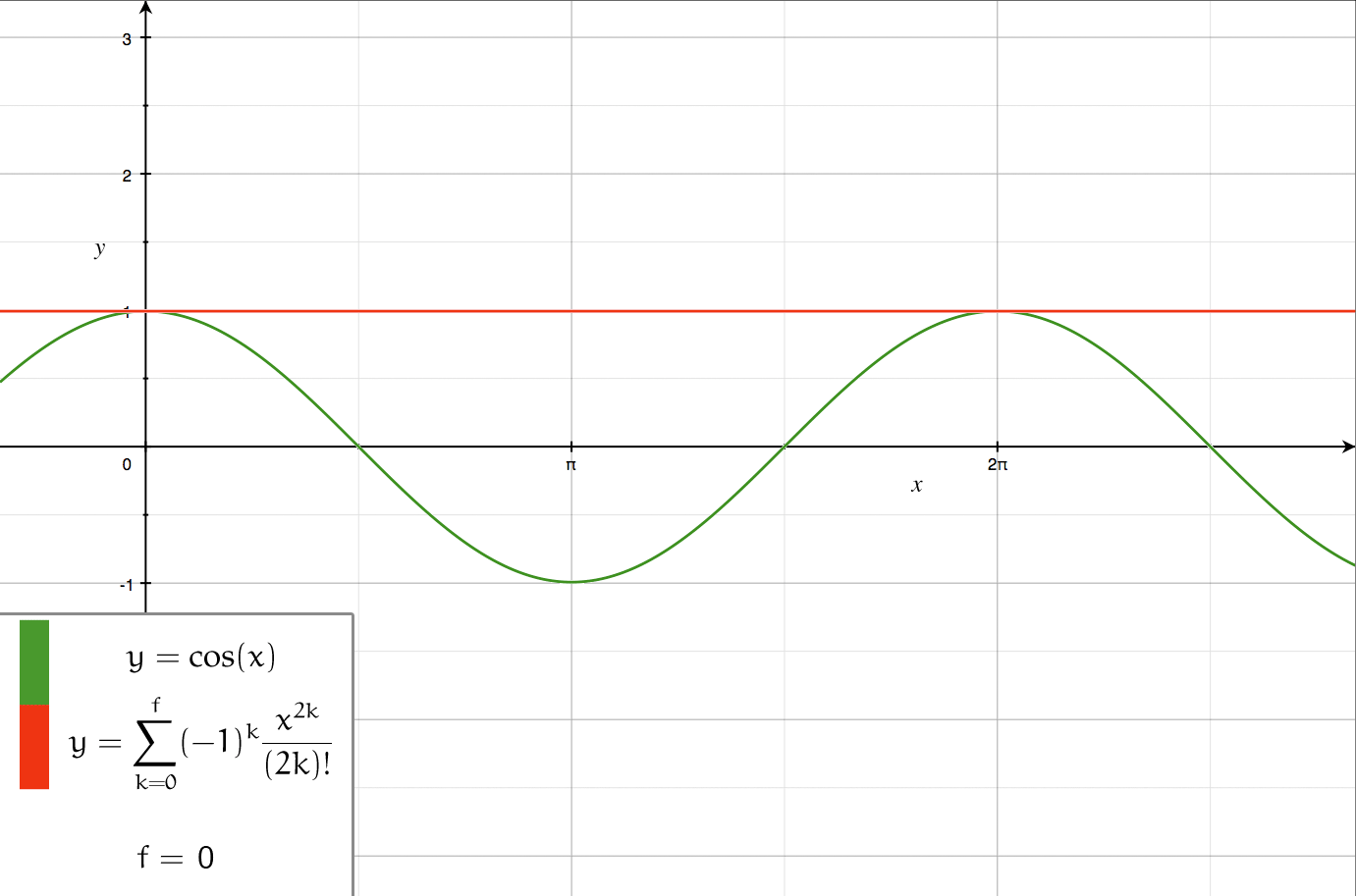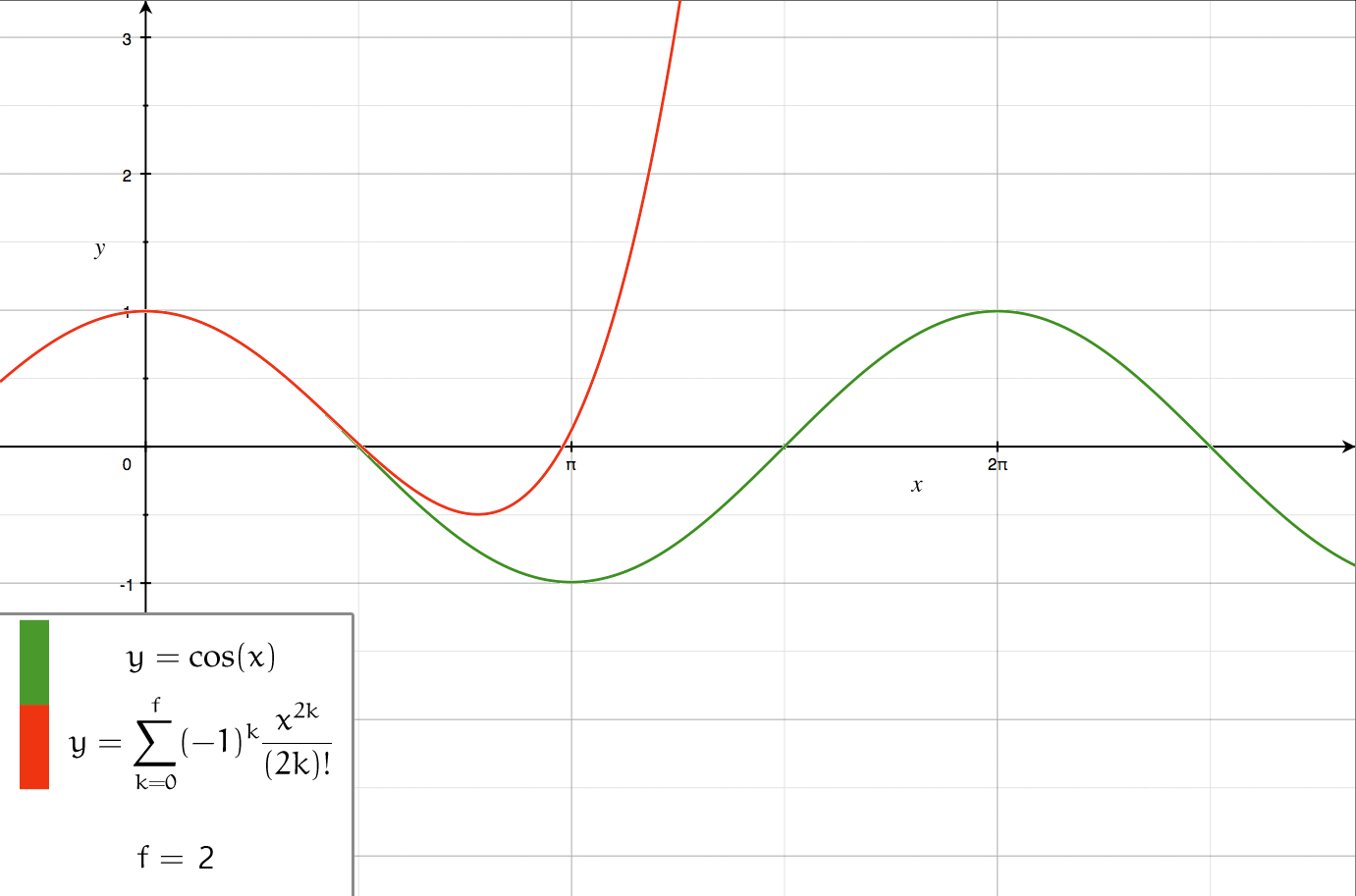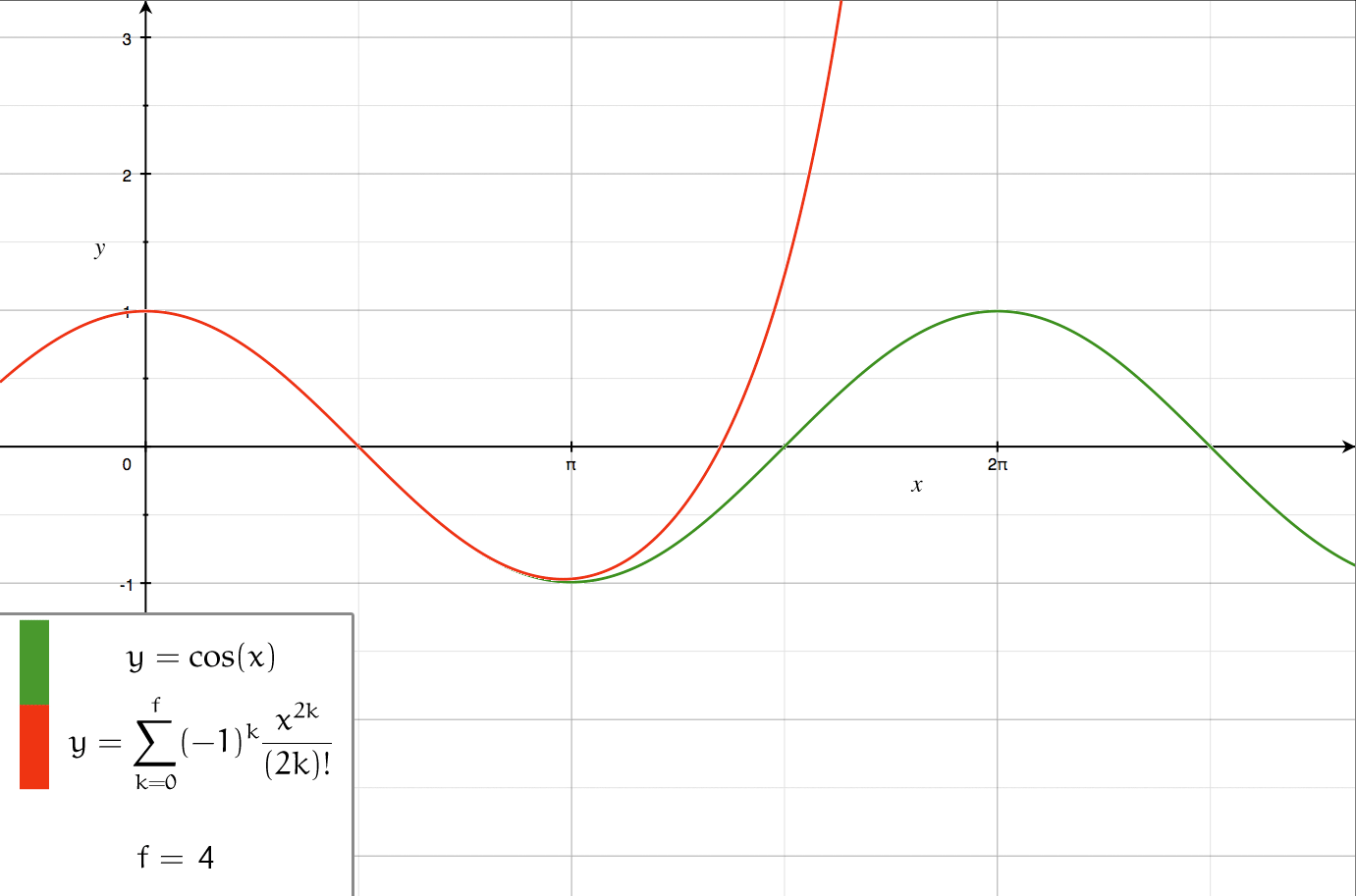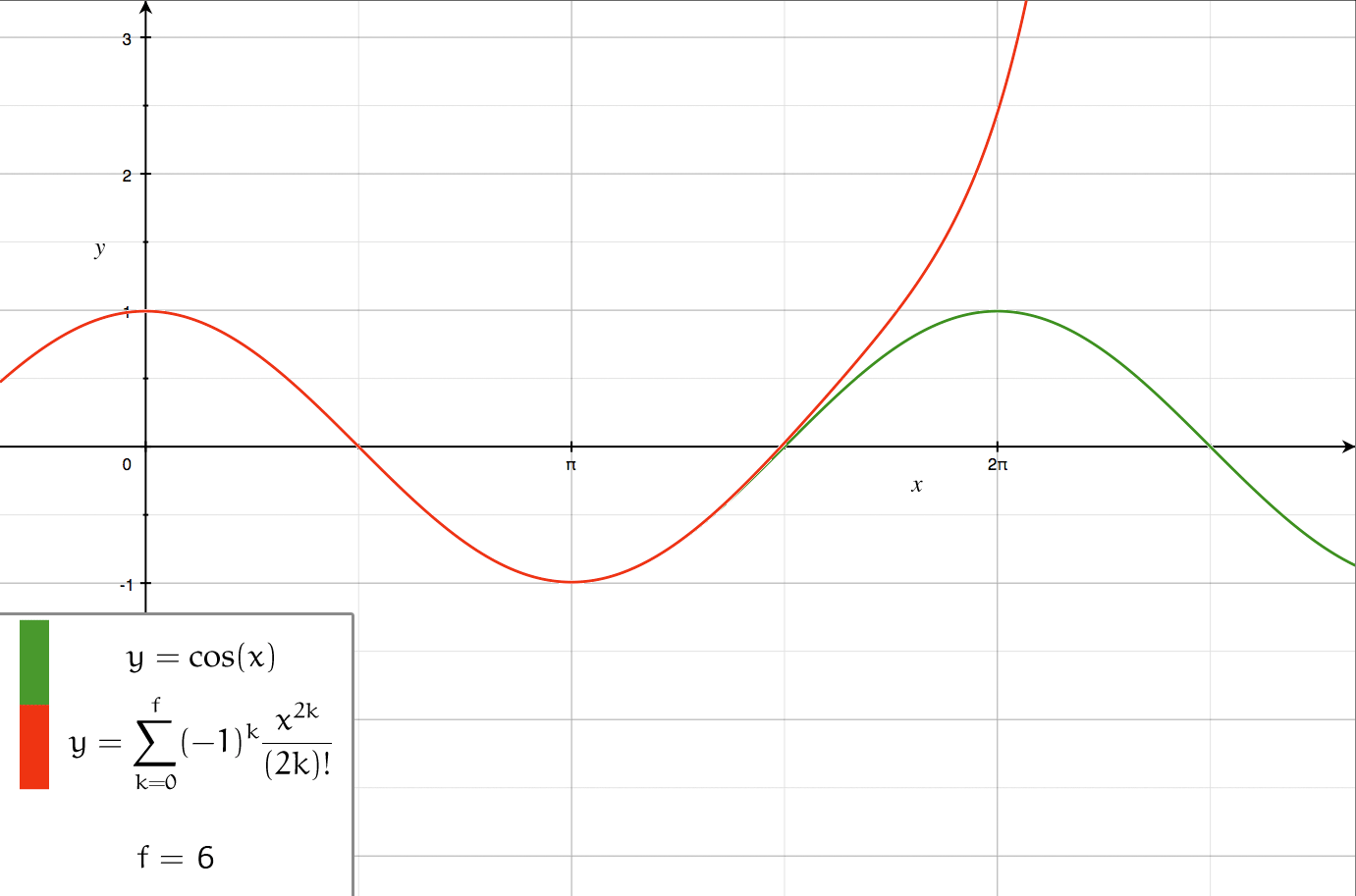
Series Expansion
In mathematics, a series expansion is a technique that expresses a Function (mathematics), function as an infinite sum, or Series (mathematics), series, of simpler functions. It is a method for calculating a Function (mathematics), function that cannot be expressed by just elementary operators (addition, subtraction, multiplication and division). The resulting so-called ''Series (mathematics), series'' often can be limited to a finite number of terms, thus yielding an approximation of the function. The fewer terms of the sequence are used, the simpler this approximation will be. Often, the resulting inaccuracy (i.e., the partial sum of the omitted terms) can be described by an equation involving Big O notation (see also asymptotic expansion). The series expansion on an open interval will also be an approximation for non-analytic functions. Types of series expansions There are several kinds of series expansions, listed below. Taylor series A ''Taylor series'' is a power ser ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Orbital Elements
Orbital elements are the parameters required to uniquely identify a specific orbit. In celestial mechanics these elements are considered in two-body systems using a Kepler orbit. There are many different ways to mathematically describe the same orbit, but certain schemes are commonly used in astronomy and orbital mechanics. A real orbit and its elements change over time due to gravitational Perturbation (astronomy), perturbations by other objects and the effects of general relativity. A Kepler orbit is an idealized, mathematical approximation of the orbit at a particular time. When viewed from an inertial frame, two orbiting bodies trace out distinct trajectories. Each of these trajectories has its Focus (geometry), focus at the common center of mass. When viewed from a non-inertial frame centered on one of the bodies, only the trajectory of the opposite body is apparent; Keplerian elements describe these non-inertial trajectories. An orbit has two sets of Keplerian elements depe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Satellite
A satellite or an artificial satellite is an object, typically a spacecraft, placed into orbit around a celestial body. They have a variety of uses, including communication relay, weather forecasting, navigation ( GPS), broadcasting, scientific research, and Earth observation. Additional military uses are reconnaissance, early warning, signals intelligence and, potentially, weapon delivery. Other satellites include the final rocket stages that place satellites in orbit and formerly useful satellites that later become defunct. Except for passive satellites, most satellites have an electricity generation system for equipment on board, such as solar panels or radioisotope thermoelectric generators (RTGs). Most satellites also have a method of communication to ground stations, called transponders. Many satellites use a standardized bus to save cost and work, the most popular of which are small CubeSats. Similar satellites can work together as groups, forming constellatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Star
A star is a luminous spheroid of plasma (physics), plasma held together by Self-gravitation, self-gravity. The List of nearest stars and brown dwarfs, nearest star to Earth is the Sun. Many other stars are visible to the naked eye at night sky, night; their immense distances from Earth make them appear as fixed stars, fixed points of light. The most prominent stars have been categorised into constellations and asterism (astronomy), asterisms, and many of the brightest stars have proper names. Astronomers have assembled star catalogues that identify the known stars and provide standardized stellar designations. The observable universe contains an estimated to stars. Only about 4,000 of these stars are visible to the naked eye—all within the Milky Way galaxy. A star's life star formation, begins with the gravitational collapse of a gaseous nebula of material largely comprising hydrogen, helium, and traces of heavier elements. Its stellar mass, total mass mainly determines it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mercury Perturbation Comparison
Mercury most commonly refers to: * Mercury (planet), the closest planet to the Sun * Mercury (element), a chemical element * Mercury (mythology), a Roman deity Mercury or The Mercury may also refer to: Companies * Mercury (toy manufacturer), a brand of diecast toy cars manufactured in Italy * Mercury Communications, a British telecommunications firm set up in the 1980s * Mercury Corporation, an American aircraft manufacturer * Mercury Cyclecar Company, a defunct American car company * Mercury Drug, a Philippine pharmacy chain * Mercury Energy, an electricity generation and retail company in New Zealand * Mercury Filmworks, a Canadian independent animation studio * Mercury General, a multiple-line American insurance organization * Mercury Interactive, a software testing tools vendor * Mercury Marine, a manufacturer of marine engines, particularly outboard motors * Mercury Systems, a defense-related information technology company * Mercury Technologies, a financial tech ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
N-body Problem
In physics, the -body problem is the problem of predicting the individual motions of a group of astronomical object, celestial objects interacting with each other gravitationally.Leimanis and Minorsky: Our interest is with Leimanis, who first discusses some history about the -body problem, especially Ms. Kovalevskaya's 1868–1888 twenty-year complex-variables approach, failure; Section 1: "The Dynamics of Rigid Bodies and Mathematical Exterior Ballistics" (Chapter 1, "The motion of a rigid body about a fixed point (Euler and Poisson equations)"; Chapter 2, "Mathematical Exterior Ballistics"), good precursor background to the -body problem; Section 2: "Celestial Mechanics" (Chapter 1, "The Uniformization of the Three-body Problem (Restricted Three-body Problem)"; Chapter 2, "Capture in the Three-Body Problem"; Chapter 3, "Generalized -body Problem"). Solving this problem has been motivated by the desire to understand the motions of the Sun, Moon, planets, and visible stars. In th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Three-body Problem
In physics, specifically classical mechanics, the three-body problem is to take the initial positions and velocities (or momenta) of three point masses orbiting each other in space and then calculate their subsequent trajectories using Newton's laws of motion and Newton's law of universal gravitation. Unlike the two-body problem, the three-body problem has no general closed-form solution, meaning there is no equation that always solves it. When three bodies orbit each other, the resulting dynamical system is chaotic for most initial conditions. Because there are no solvable equations for most three-body systems, the only way to predict the motions of the bodies is to estimate them using numerical methods. The three-body problem is a special case of the -body problem. Historically, the first specific three-body problem to receive extended study was the one involving the Earth, the Moon, and the Sun. In an extended modern sense, a three-body problem is any problem in cl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |