|
Evasive Boolean Function
In mathematics, an evasive Boolean function f (of n variables) is a Boolean function for which every decision tree algorithm has running time of exactly n. Consequently, every decision tree algorithm that represents the function has, at worst case, a running time of n. Definition The type of algorithms considered in the definition of evasive Boolean function are decision trees in which each internal node tests the value of one of the given Boolean variables, and branches accordingly. Each leaf node of the tree specifies the value of the function for inputs that reach that node. The worst case decision tree complexity of a given decision tree is the number of variables examined on the longest root-to-leaf path of the tree. Every n-variable function has a decision tree algorithm that examines exactly n variables on all inputs, using a decision tree in which all nodes at level i test the ith variable. A function is evasive if no other decision tree for the same function has smaller ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boolean Function
In mathematics, a Boolean function is a function whose arguments and result assume values from a two-element set (usually , or ). Alternative names are switching function, used especially in older computer science literature, and truth function (or logical function), used in logic. Boolean functions are the subject of Boolean algebra and switching theory. A Boolean function takes the form f:\^k \to \, where \ is known as the Boolean domain and k is a non-negative integer called the arity of the function. In the case where k=0, the function is a constant element of \. A Boolean function with multiple outputs, f:\^k \to \^m with m>1 is a vectorial or ''vector-valued'' Boolean function (an S-box in symmetric cryptography). There are 2^ different Boolean functions with k arguments; equal to the number of different truth tables with 2^k entries. Every k-ary Boolean function can be expressed as a propositional formula in k variables x_1,...,x_k, and two propositional formulas a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decision Tree Model
In computational complexity theory, the decision tree model is the model of computation in which an algorithm can be considered to be a decision tree, i.e. a sequence of ''queries'' or ''tests'' that are done adaptively, so the outcome of previous tests can influence the tests performed next. Typically, these tests have a small number of outcomes (such as a yes–no question) and can be performed quickly (say, with unit computational cost), so the worst-case time complexity of an algorithm in the decision tree model corresponds to the depth of the corresponding tree. This notion of computational complexity of a problem or an algorithm in the decision tree model is called its decision tree complexity or query complexity. Decision tree models are instrumental in establishing lower bounds for the complexity of certain classes of computational problems and algorithms. Several variants of decision tree models have been introduced, depending on the computational model and type of quer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
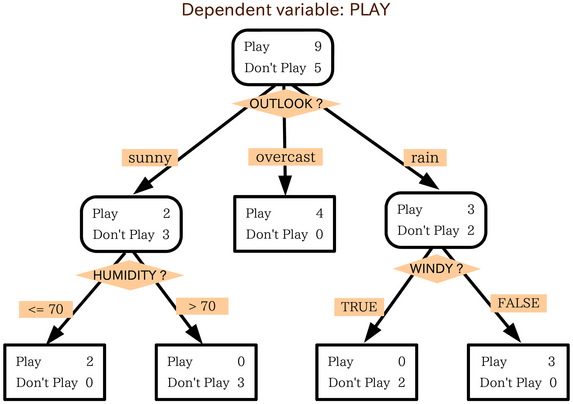
Decision Tree
A decision tree is a decision support system, decision support recursive partitioning structure that uses a Tree (graph theory), tree-like Causal model, model of decisions and their possible consequences, including probability, chance event outcomes, resource costs, and utility. It is one way to display an algorithm that only contains conditional control statements. Decision trees are commonly used in operations research, specifically in decision analysis, to help identify a strategy most likely to reach a goal, but are also a popular tool in Decision tree learning, machine learning. Overview A decision tree is a flowchart-like structure in which each internal node represents a test on an attribute (e.g. whether a coin flip comes up heads or tails), each branch represents the outcome of the test, and each leaf node represents a class label (decision taken after computing all attributes). The paths from root to leaf represent classification rules. In decision analysis, a de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decision Tree Complexity
In computational complexity theory, the decision tree model is the model of computation in which an algorithm can be considered to be a decision tree, i.e. a sequence of ''queries'' or ''tests'' that are done adaptively, so the outcome of previous tests can influence the tests performed next. Typically, these tests have a small number of outcomes (such as a yes–no question) and can be performed quickly (say, with unit computational cost), so the worst-case time complexity of an algorithm in the decision tree model corresponds to the depth of the corresponding tree. This notion of computational complexity of a problem or an algorithm in the decision tree model is called its decision tree complexity or query complexity. Decision tree models are instrumental in establishing lower bounds for the complexity of certain classes of computational problems and algorithms. Several variants of decision tree models have been introduced, depending on the computational model and type of quer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logical And
In logic, mathematics and linguistics, ''and'' (\wedge) is the truth-functional operator of conjunction or logical conjunction. The logical connective of this operator is typically represented as \wedge or \& or K (prefix) or \times or \cdot in which \wedge is the most modern and widely used. The ''and'' of a set of operands is true if and only if ''all'' of its operands are true, i.e., A \land B is true if and only if A is true and B is true. An operand of a conjunction is a conjunct. Beyond logic, the term "conjunction" also refers to similar concepts in other fields: * In natural language, the denotation of expressions such as English " and"; * In programming languages, the short-circuit and control structure; * In set theory, intersection. * In lattice theory, logical conjunction ( greatest lower bound). Notation And is usually denoted by an infix operator: in mathematics and logic, it is denoted by a "wedge" \wedge (Unicode ), \& or \times; in electronics, \cdot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logical Or
In logic, disjunction (also known as logical disjunction, logical or, logical addition, or inclusive disjunction) is a logical connective typically notated as \lor and read aloud as "or". For instance, the English language, English language sentence "it is sunny or it is warm" can be represented in logic using the disjunctive formula S \lor W , assuming that S abbreviates "it is sunny" and W abbreviates "it is warm". In classical logic, disjunction is given a truth functional semantics according to which a formula \phi \lor \psi is true unless both \phi and \psi are false. Because this semantics allows a disjunctive formula to be true when both of its disjuncts are true, it is an ''inclusive'' interpretation of disjunction, in contrast with exclusive disjunction. Classical proof theory, proof theoretical treatments are often given in terms of rules such as disjunction introduction and disjunction elimination. Disjunction has also been given numerous nonclassical logic, non- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Algorithm
An algorithm is fundamentally a set of rules or defined procedures that is typically designed and used to solve a specific problem or a broad set of problems. Broadly, algorithms define process(es), sets of rules, or methodologies that are to be followed in calculations, data processing, data mining, pattern recognition, automated reasoning or other problem-solving operations. With the increasing automation of services, more and more decisions are being made by algorithms. Some general examples are; risk assessments, anticipatory policing, and pattern recognition technology. The following is a list of well-known algorithms. Automated planning Combinatorial algorithms General combinatorial algorithms * Cycle detection#Brent's algorithm, Brent's algorithm: finds a cycle in function value iterations using only two iterators * Floyd's cycle-finding algorithm: finds a cycle in function value iterations * Gale–Shapley algorithm: solves the stable matching problem * Pseudorandom nu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Implicit Graph
In the study of graph algorithms, an implicit graph representation (or more simply implicit graph) is a Graph (discrete mathematics), graph whose vertex (graph theory), vertices or edges are not represented as explicit objects in a computer's memory, but rather are determined algorithmically from some other input, for example a computable function. Neighborhood representations The notion of an implicit graph is common in various search algorithms which are described in terms of graphs. In this context, an implicit graph may be defined as a set of rules to define all Neighborhood (graph theory), neighbors for any specified vertex. This type of implicit graph representation is analogous to an adjacency list, in that it provides easy access to the neighbors of each vertex. For instance, in searching for a solution to a puzzle such as Rubik's Cube, one may define an implicit graph in which each vertex represents one of the possible states of the cube, and each edge represents a move ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aanderaa–Karp–Rosenberg Conjecture
In theoretical computer science, the Aanderaa–Karp–Rosenberg conjecture (also known as the Aanderaa–Rosenberg conjecture or the evasiveness conjecture) is a group of related conjectures about the number of questions of the form "Is there an edge between vertex u and vertex v?" that have to be answered to determine whether or not an undirected graph has a particular property such as planarity or bipartiteness. They are named after Stål Aanderaa, Richard M. Karp, and Arnold L. Rosenberg. According to the conjecture, for a wide class of properties, no algorithm can guarantee that it will be able to skip any questions: any algorithm for determining whether the graph has the property, no matter how clever, might need to examine every pair of vertices before it can give its answer. A property satisfying this conjecture is called evasive. More precisely, the Aanderaa–Rosenberg conjecture states that any deterministic algorithm must test at least a constant fraction of all p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theoretical Computer Science (journal)
''Theoretical Computer Science'' (''TCS'') is a computer science journal published by Elsevier, started in 1975 and covering theoretical computer science. The journal publishes 52 issues a year. It is abstracted and indexed by Scopus and the Science Citation Index. According to the Journal Citation Reports, its 2020 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a type of journal ranking. Journals with higher impact factor values are considered more prestigious or important within their field. The Impact Factor of a journa ... is 0.827. References Computer science journals Elsevier academic journals Academic journals established in 1975 {{comp-sci-theory-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Power
In mathematics, a prime power is a positive integer which is a positive integer power of a single prime number. For example: , and are prime powers, while , and are not. The sequence of prime powers begins: 2, 3, 4, 5, 7, 8, 9, 11, 13, 16, 17, 19, 23, 25, 27, 29, 31, 32, 37, 41, 43, 47, 49, 53, 59, 61, 64, 67, 71, 73, 79, 81, 83, 89, 97, 101, 103, 107, 109, 113, 121, 125, 127, 128, 131, 137, 139, 149, 151, 157, 163, 167, 169, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 243, 251, … . The prime powers are those positive integers that are divisible by exactly one prime number; in particular, the number 1 is not a prime power. Prime powers are also called primary numbers, as in the primary decomposition. Properties Algebraic properties Prime powers are powers of prime numbers. Every prime power (except powers of 2 greater than 4) has a primitive root; thus the multiplicative group of integers modulo ''p''''n'' (that is, the group of units of the ri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |