Decision Tree Complexity on:
[Wikipedia]
[Google]
[Amazon]
 In
In
 In
In computational complexity theory
In theoretical computer science and mathematics, computational complexity theory focuses on classifying computational problems according to their resource usage, and explores the relationships between these classifications. A computational problem ...
, the decision tree model is the model of computation
In computer science, and more specifically in computability theory and computational complexity theory, a model of computation is a model which describes how an output of a mathematical function is computed given an input. A model describes how ...
in which an algorithm
In mathematics and computer science, an algorithm () is a finite sequence of Rigour#Mathematics, mathematically rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algo ...
can be considered to be a decision tree
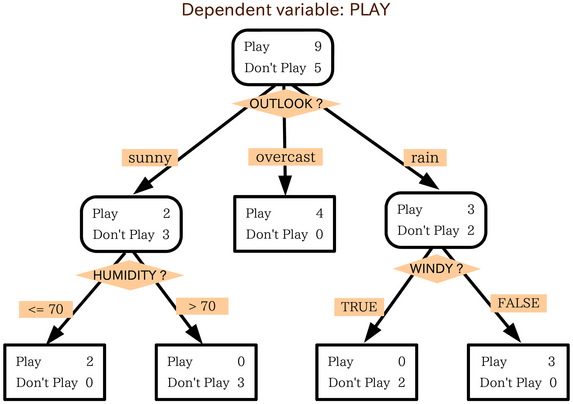
A decision tree is a decision support system, decision support recursive partitioning structure that uses a Tree (graph theory), tree-like Causal model, model of decisions and their possible consequences, including probability, chance event ou ...
, i.e. a sequence of ''queries'' or ''tests'' that are done adaptively, so the outcome of previous tests can influence the tests performed next.
Typically, these tests have a small number of outcomes (such as a yes–no question
In linguistics, a yes–no question, also known as a binary question, a polar question, or a general question, is a closed-ended question whose expected answer is one of two choices, one that provides an affirmative answer to the question versus ...
) and can be performed quickly (say, with unit computational cost), so the worst-case time complexity
In theoretical computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations ...
of an algorithm in the decision tree model corresponds to the depth of the corresponding tree. This notion of computational complexity of a problem or an algorithm in the decision tree model is called its decision tree complexity or query complexity.
Decision tree models are instrumental in establishing lower bound
In mathematics, particularly in order theory, an upper bound or majorant of a subset of some preordered set is an element of that is every element of .
Dually, a lower bound or minorant of is defined to be an element of that is less th ...
s for the complexity of certain classes of computational problems and algorithms. Several variants of decision tree models have been introduced, depending on the computational model
A computational model uses computer programs to simulate and study complex systems using an algorithmic or mechanistic approach and is widely used in a diverse range of fields spanning from physics, engineering, chemistry and biology to economics ...
and type of query algorithms are allowed to perform.
For example, a decision tree argument is used to show that a comparison sort
A comparison sort is a type of sorting algorithm that only reads the list elements through a single abstract comparison operation (often a "less than or equal to" operator or a three-way comparison) that determines which of two elements should oc ...
of items must make comparisons. For comparison sorts, a query is a comparison of two items , with two outcomes (assuming no items are equal): either or . Comparison sorts can be expressed as decision trees in this model, since such sorting algorithms only perform these types of queries.
Comparison trees and lower bounds for sorting
Decision trees are often employed to understand algorithms for sorting and other similar problems; this was first done by Ford and Johnson. For example, many sorting algorithms arecomparison sort
A comparison sort is a type of sorting algorithm that only reads the list elements through a single abstract comparison operation (often a "less than or equal to" operator or a three-way comparison) that determines which of two elements should oc ...
s, which means that they only gain information about an input sequence via local comparisons: testing whether , , or . Assuming that the items to be sorted are all distinct and comparable, this can be rephrased as a yes-or-no question: is ?
These algorithms can be modeled as binary decision trees, where the queries are comparisons: an internal node corresponds to a query, and the node's children correspond to the next query when the answer to the question is yes or no. For leaf nodes, the output corresponds to a permutation
In mathematics, a permutation of a set can mean one of two different things:
* an arrangement of its members in a sequence or linear order, or
* the act or process of changing the linear order of an ordered set.
An example of the first mean ...
that describes how the input sequence was scrambled from the fully ordered list of items. (The inverse of this permutation, , re-orders the input sequence.)
One can show that comparison sorts must use comparisons through a simple argument: for an algorithm to be correct, it must be able to output every possible permutation of elements; otherwise, the algorithm would fail for that particular permutation as input. So, its corresponding decision tree must have at least as many leaves as permutations: leaves. Any binary tree with at least leaves has depth at least , so this is a lower bound on the run time of a comparison sorting algorithm. In this case, the existence of numerous comparison-sorting algorithms having this time complexity, such as mergesort
In computer science, merge sort (also commonly spelled as mergesort and as ) is an efficient, general-purpose, and comparison-based sorting algorithm. Most implementations of merge sort are stable, which means that the relative order of equal el ...
and heapsort
In computer science, heapsort is an efficient, comparison-based sorting algorithm that reorganizes an input array into a heap (a data structure where each node is greater than its children) and then repeatedly removes the largest node from that ...
, demonstrates that the bound is tight.
This argument does not use anything about the type of query, so it in fact proves a lower bound for any sorting algorithm that can be modeled as a binary decision tree. In essence, this is a rephrasing of the information-theoretic argument that a correct sorting algorithm must learn at least bits of information about the input sequence. As a result, this also works for randomized decision trees as well.
Other decision tree lower bounds do use that the query is a comparison. For example, consider the task of only using comparisons to find the smallest number among numbers. Before the smallest number can be determined, every number except the smallest must "lose" (compare greater) in at least one comparison. So, it takes at least comparisons to find the minimum. (The information-theoretic argument here only gives a lower bound of .) A similar argument works for general lower bounds for computing order statistic
In statistics, the ''k''th order statistic of a statistical sample is equal to its ''k''th-smallest value. Together with Ranking (statistics), rank statistics, order statistics are among the most fundamental tools in non-parametric statistics and ...
s.
Linear and algebraic decision trees
Linear decision trees generalize the above comparison decision trees to computing functions that take real vectors as input. The tests in linear decision trees are linear functions: for a particular choice of real numbers , output the sign of . (Algorithms in this model can only depend on the sign of the output.) Comparison trees are linear decision trees, because the comparison between and corresponds to the linear function . From its definition, linear decision trees can only specify functions whosefibers
Fiber (spelled fibre in British English; from ) is a natural or artificial substance that is significantly longer than it is wide. Fibers are often used in the manufacture of other materials. The strongest engineering materials often inco ...
can be constructed by taking unions and intersections of half-spaces.
''Algebraic decision trees'' are a generalization of linear decision trees that allow the test functions to be polynomials of degree . Geometrically, the space is divided into semi-algebraic sets (a generalization of hyperplane).
These decision tree models, defined by Rabin and Reingold, are often used for proving lower bounds in computational geometry. For example, Ben-Or showed that element uniqueness (the task of computing , where is 0 if and only if there exist distinct coordinates such that ) requires an algebraic decision tree of depth . This was first showed for linear decision models by Dobkin and Lipton. They also show a lower bound for linear decision trees on the knapsack problem, generalized to algebraic decision trees by Steele and Yao.
Boolean decision tree complexities
For Boolean decision trees, the task is to compute the value of an n-bitBoolean function
In mathematics, a Boolean function is a function whose arguments and result assume values from a two-element set (usually , or ). Alternative names are switching function, used especially in older computer science literature, and truth functi ...
for an input . The queries correspond to reading a bit of the input, , and the output is . Each query may be dependent on previous queries. There are many types of computational models using decision trees that could be considered, admitting multiple complexity notions, called ''complexity measures''.
Deterministic decision tree
If the output of a decision tree is , for all , the decision tree is said to "compute" . The depth of a tree is the maximum number of queries that can happen before a leaf is reached and a result obtained. , the ''deterministic decision tree'' complexity of is the smallest depth among all deterministic decision trees that compute .Randomized decision tree
One way to define a ''randomized decision tree'' is to add additional nodes to the tree, each controlled by a probability . Another equivalent definition is to define it as a distribution over deterministic decision trees. Based on this second definition, the complexity of the randomized tree is defined as the largest depth among all the trees in the support of the underlying distribution. is defined as the complexity of the lowest-depth randomized decision tree whose result is with probability at least for all (i.e., with bounded 2-sided error). is known as theMonte Carlo
Monte Carlo ( ; ; or colloquially ; , ; ) is an official administrative area of Monaco, specifically the Ward (country subdivision), ward of Monte Carlo/Spélugues, where the Monte Carlo Casino is located. Informally, the name also refers to ...
randomized decision-tree complexity, because the result is allowed to be incorrect with bounded two-sided error. The Las Vegas
Las Vegas, colloquially referred to as Vegas, is the most populous city in the U.S. state of Nevada and the county seat of Clark County. The Las Vegas Valley metropolitan area is the largest within the greater Mojave Desert, and second-l ...
decision-tree complexity measures the ''expected'' depth of a decision tree that must be correct (i.e., has zero-error). There is also a one-sided bounded-error version which is denoted by .
Nondeterministic decision tree
The nondeterministic decision tree complexity of a function is known more commonly as the certificate complexity of that function. It measures the number of input bits that anondeterministic algorithm
In computer science and computer programming, a nondeterministic algorithm is an algorithm that, even for the same input, can exhibit different behaviors on different runs, as opposed to a deterministic algorithm.
Different models of computation ...
would need to look at in order to evaluate the function with certainty.
Formally, the certificate complexity of at is the size of the smallest subset of indices