|
Electroosmotic Flow
In chemistry, electro-osmotic flow (EOF, hyphen optional; synonymous with electro-osmosis or electro-endosmosis) is the motion of liquid induced by an applied potential across a porous material, capillary tube, membrane, microchannel, or any other fluid conduit. Because electro-osmotic velocities are independent of conduit size, as long as the electrical double layer is much smaller than the characteristic length scale of the channel, electro-osmotic flow will have little effect. Electro-osmotic flow is most significant when in small channels, and is an essential component in chemical separation techniques, notably capillary electrophoresis. Electro-osmotic flow can occur in natural unfiltered water, as well as buffered solutions. History Electro-osmotic flow was first reported in 1807 by Ferdinand Friedrich Reuss (18 February 1778 (Tübingen, Germany) – 14 April 1852 (Stuttgart, Germany)) in an unpublished lecture before the Physical-Medical Society of Moscow; Reuss firs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chemistry
Chemistry is the scientific study of the properties and behavior of matter. It is a physical science within the natural sciences that studies the chemical elements that make up matter and chemical compound, compounds made of atoms, molecules and ions: their composition, structure, properties, behavior and the changes they undergo during chemical reaction, reactions with other chemical substance, substances. Chemistry also addresses the nature of chemical bonds in chemical compounds. In the scope of its subject, chemistry occupies an intermediate position between physics and biology. It is sometimes called the central science because it provides a foundation for understanding both Basic research, basic and Applied science, applied scientific disciplines at a fundamental level. For example, chemistry explains aspects of plant growth (botany), the formation of igneous rocks (geology), how atmospheric ozone is formed and how environmental pollutants are degraded (ecology), the prop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
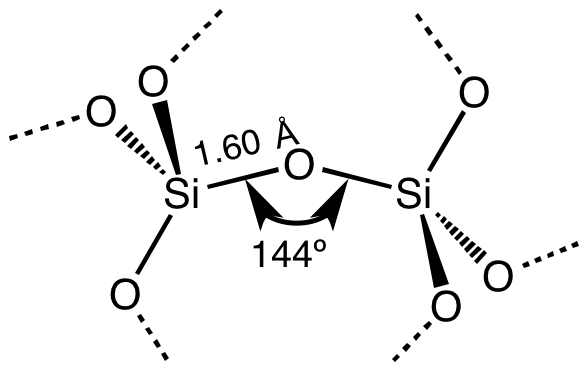
Silica
Silicon dioxide, also known as silica, is an oxide of silicon with the chemical formula , commonly found in nature as quartz. In many parts of the world, silica is the major constituent of sand. Silica is one of the most complex and abundant families of materials, existing as a compound of several minerals and as a synthetic product. Examples include fused quartz, fumed silica, opal, and aerogels. It is used in structural materials, microelectronics, and as components in the food and pharmaceutical industries. All forms are white or colorless, although impure samples can be colored. Silicon dioxide is a common fundamental constituent of glass. Structure In the majority of silicon dioxides, the silicon atom shows Tetrahedral molecular geometry, tetrahedral coordination, with four oxygen atoms surrounding a central Si atomsee 3-D Unit Cell. Thus, SiO2 forms 3-dimensional network solids in which each silicon atom is covalently bonded in a tetrahedral manner to 4 oxygen atoms. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Debye–Hückel Theory
The Debye–Hückel theory was proposed by Peter Debye and Erich Hückel as a theoretical explanation for departures from ideality in solutions of electrolytes and plasmas. It is a linearized Poisson–Boltzmann model, which assumes an extremely simplified model of electrolyte solution but nevertheless gave accurate predictions of mean activity coefficients for ions in dilute solution. The Debye–Hückel equation provides a starting point for modern treatments of non-ideality of electrolyte solutions. Overview In the chemistry of electrolyte solutions, an ideal solution is a solution whose colligative properties are proportional to the concentration of the solute. Real solutions may show departures from this kind of ideality. In order to accommodate these effects in the thermodynamics of solutions, the concept of activity was introduced: the properties are then proportional to the activities of the ions. Activity ''a'' is proportional to concentration ''c'', with the proport ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vacuum Permittivity
Vacuum permittivity, commonly denoted (pronounced "epsilon nought" or "epsilon zero"), is the value of the absolute dielectric permittivity of classical vacuum. It may also be referred to as the permittivity of free space, the electric constant, or the distributed capacitance of the vacuum. It is an ideal (baseline) physical constant. Its CODATA value is: It is a measure of how dense of an electric field is "permitted" to form in response to electric charges and relates the units for electric charge to mechanical quantities such as length and force. For example, the force between two separated electric charges with spherical symmetry (in the vacuum of classical electromagnetism) is given by Coulomb's law: F_\text = \frac \frac Here, ''q''1 and ''q''2 are the charges, ''r'' is the distance between their centres, and the value of the constant fraction 1/(4π''ε''0) is approximately . Likewise, ''ε''0 appears in Maxwell's equations, which describe the properties of electr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplace’s Equation
In mathematics and physics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace, who first studied its properties in 1786. This is often written as \nabla^2\! f = 0 or \Delta f = 0, where \Delta = \nabla \cdot \nabla = \nabla^2 is the Laplace operator,The delta symbol, Δ, is also commonly used to represent a finite change in some quantity, for example, \Delta x = x_1 - x_2. Its use to represent the Laplacian should not be confused with this use. \nabla \cdot is the divergence operator (also symbolized "div"), \nabla is the gradient operator (also symbolized "grad"), and f (x, y, z) is a twice-differentiable real-valued function. The Laplace operator therefore maps a scalar function to another scalar function. If the right-hand side is specified as a given function, h(x, y, z), we have \Delta f = h This is called Poisson's equation, a generalization of Laplace's equation. Laplace's equation and Poisson's equation are the simple ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zeta Potential
Zeta potential is the electrical potential at the slipping plane. This plane is the interface which separates mobile fluid from fluid that remains attached to the surface.is a scientific term for Electrokinetic phenomena, electrokinetic Electric potential, potential in colloidal Dispersion (chemistry), dispersions. In the colloidal chemistry literature, it is usually denoted using the Greek letter zeta, zeta (ζ), hence ''ζ-potential''. The usual units are Volt, volts (V) or, more commonly, millivolts (mV). From a theoretical viewpoint, the zeta potential is the electric potential in the interfacial double layer (interfacial), double layer (DL) at the location of the slipping plane relative to a point in the bulk fluid away from the interface. In other words, zeta potential is the potential difference between the dispersion medium and the stationary layer of fluid attached to the dispersed particle. The zeta potential is caused by the net Electric charge, electrical charge conta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Material Derivative
In continuum mechanics, the material derivative describes the time rate of change of some physical quantity (like heat or momentum) of a material element that is subjected to a space-and-time-dependent macroscopic velocity field. The material derivative can serve as a link between Eulerian and Lagrangian descriptions of continuum deformation. For example, in fluid dynamics, the velocity field is the flow velocity, and the quantity of interest might be the temperature of the fluid. In this case, the material derivative then describes the temperature change of a certain fluid parcel with time, as it flows along its pathline (trajectory). Other names There are many other names for the material derivative, including: *advective derivative *convective derivative *derivative following the motion *hydrodynamic derivative *Lagrangian derivative *particle derivative *substantial derivative *substantive derivative *Stokes derivative *total derivative, although the material derivati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Momentum
In Newtonian mechanics, momentum (: momenta or momentums; more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. If is an object's mass and is its velocity (also a vector quantity), then the object's momentum (from Latin '' pellere'' "push, drive") is: \mathbf = m \mathbf. In the International System of Units (SI), the unit of measurement of momentum is the kilogram metre per second (kg⋅m/s), which is dimensionally equivalent to the newton-second. Newton's second law of motion states that the rate of change of a body's momentum is equal to the net force acting on it. Momentum depends on the frame of reference, but in any inertial frame of reference, it is a ''conserved'' quantity, meaning that if a closed system is not affected by external forces, its total momentum does not change. Momentum is also conserved in special relativity (with a mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuity Equation
A continuity equation or transport equation is an equation that describes the transport of some quantity. It is particularly simple and powerful when applied to a conserved quantity, but it can be generalized to apply to any extensive quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described using continuity equations. Continuity equations are a stronger, local form of conservation laws. For example, a weak version of the law of conservation of energy states that energy can neither be created nor destroyed—i.e., the total amount of energy in the universe is fixed. This statement does not rule out the possibility that a quantity of energy could disappear from one point while simultaneously appearing at another point. A stronger statement is that energy is ''locally'' conserved: energy can neither be created nor destroyed, ''nor'' can it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plug Flow
In fluid mechanics, plug flow is a simple model of the velocity profile of a fluid flowing in a pipe. In plug flow, the velocity of the fluid is assumed to be constant across any cross-section of the pipe perpendicular to the axis of the pipe. The plug flow model assumes there is no boundary layer adjacent to the inner wall of the pipe. The plug flow model has many practical applications. One example is in the design of chemical reactors. Essentially no back mixing is assumed with "plugs" of fluid passing through the reactor. This results in differential equations that need to be integrated to find the reactor conversion and outlet temperatures. Other simplifications used are perfect radial mixing and a homogeneous bed structure. An advantage of the plug flow model is that no part of the solution of the problem can be perpetuated "upstream". This allows one to calculate the exact solution to the differential equation knowing only the initial conditions. No further iterati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chemical Equilibrium
In a chemical reaction, chemical equilibrium is the state in which both the Reagent, reactants and Product (chemistry), products are present in concentrations which have no further tendency to change with time, so that there is no observable change in the properties of the Thermodynamic system, system. This state results when the forward reaction proceeds at the same rate as the Reversible reaction, reverse reaction. The reaction rates of the forward and backward reactions are generally not zero, but they are equal. Thus, there are no net changes in the concentrations of the reactants and products. Such a state is known as dynamic equilibrium. It is the subject of study of ''equilibrium chemistry''. Historical introduction The Concept learning, concept of chemical equilibrium was developed in 1803, after Claude Louis Berthollet, Berthollet found that some chemical reactions are Reversible reaction, reversible. For any reaction mixture to exist at equilibrium, the reaction rate, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electric Charge
Electric charge (symbol ''q'', sometimes ''Q'') is a physical property of matter that causes it to experience a force when placed in an electromagnetic field. Electric charge can be ''positive'' or ''negative''. Like charges repel each other and unlike charges attract each other. An object with no net charge is referred to as neutral particle, electrically neutral. Early knowledge of how charged substances interact is now called classical electrodynamics, and is still accurate for problems that do not require consideration of quantum mechanics, quantum effects. In an isolated system, the total charge stays the same - the amount of positive charge minus the amount of negative charge does not change over time. Electric charge is carried by subatomic particles. In ordinary matter, negative charge is carried by electrons, and positive charge is carried by the protons in the atomic nucleus, nuclei of atoms. If there are more electrons than protons in a piece of matter, it will have a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |