|
Conference Graph
In the mathematical area of graph theory, a conference graph is a strongly regular graph with parameters ''v'', and It is the graph associated with a symmetric conference matrix, and consequently its order ''v'' must be 1 (modulo 4) and a sum of two squares. Conference graphs are known to exist for all small values of ''v'' allowed by the restrictions, e.g., ''v'' = 5, 9, 13, 17, 25, 29, and (the Paley graph In mathematics, Paley graphs are undirected graphs constructed from the members of a suitable finite field by connecting pairs of elements that differ by a quadratic residue. The Paley graphs form an infinite family of conference graphs, which yiel ...s) for all prime powers congruent to 1 (modulo 4). However, there are many values of ''v'' that are allowed, for which the existence of a conference graph is unknown. The eigenvalues of a conference graph need not be integers, unlike those of other strongly regular graphs. If the graph is connected, the eigenvalues are '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Graph Theory
In mathematics and computer science, graph theory is the study of ''graph (discrete mathematics), graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of ''Vertex (graph theory), vertices'' (also called ''nodes'' or ''points'') which are connected by ''Glossary of graph theory terms#edge, edges'' (also called ''arcs'', ''links'' or ''lines''). A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics. Definitions Definitions in graph theory vary. The following are some of the more basic ways of defining graphs and related mathematical structures. Graph In one restricted but very common sense of the term, a graph is an ordered pair G=(V,E) comprising: * V, a Set (mathematics), set of vertices (also called nodes or points); * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
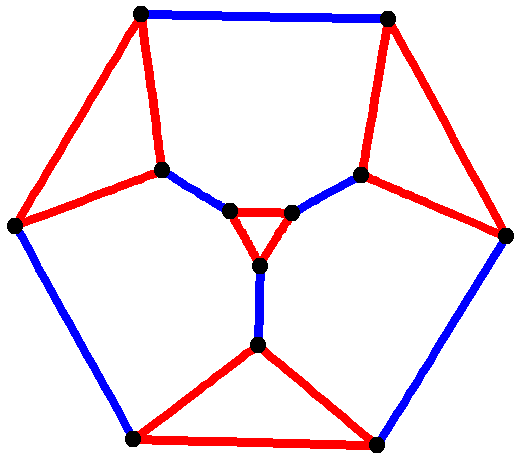
Strongly Regular Graph
In graph theory, a strongly regular graph (SRG) is a regular graph with vertices and degree such that for some given integers \lambda, \mu \ge 0 * every two adjacent vertices have common neighbours, and * every two non-adjacent vertices have common neighbours. Such a strongly regular graph is denoted by . Its complement graph is also strongly regular: it is an . A strongly regular graph is a distance-regular graph with diameter 2 whenever μ is non-zero. It is a locally linear graph whenever . Etymology A strongly regular graph is denoted as an srg(''v'', ''k'', λ, μ) in the literature. By convention, graphs which satisfy the definition trivially are excluded from detailed studies and lists of strongly regular graphs. These include the disjoint union of one or more equal-sized complete graphs, and their complements, the complete multipartite graphs with equal-sized independent sets. Andries Brouwer and Hendrik van Maldeghem (see #References) use an alternate bu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Conference Matrix
In mathematics, a conference matrix (also called a C-matrix) is a square matrix ''C'' with 0 on the diagonal and +1 and −1 off the diagonal, such that ''C''T''C'' is a multiple of the identity matrix ''I''. Thus, if the matrix (mathematics), matrix has order ''n'', ''C''T''C'' = (''n''−1)''I''. Some authors use a more general definition, which requires there to be a single 0 in each row and column but not necessarily on the diagonal. Conference matrices first arose in connection with a problem in telephony. They were first described by Vitold Belevitch, who also gave them their name. Belevitch was interested in constructing ideal telephone conference networks from ideal transformers and discovered that such networks were represented by conference matrices, hence the name. Other applications are in statistics, and another is in elliptic geometry. For ''n'' > 1, there are two kinds of conference matrix. Let us normalize ''C'' by, first (if the more ge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Modular Arithmetic
In mathematics, modular arithmetic is a system of arithmetic operations for integers, other than the usual ones from elementary arithmetic, where numbers "wrap around" when reaching a certain value, called the modulus. The modern approach to modular arithmetic was developed by Carl Friedrich Gauss in his book '' Disquisitiones Arithmeticae'', published in 1801. A familiar example of modular arithmetic is the hour hand on a 12-hour clock. If the hour hand points to 7 now, then 8 hours later it will point to 3. Ordinary addition would result in , but 15 reads as 3 on the clock face. This is because the hour hand makes one rotation every 12 hours and the hour number starts over when the hour hand passes 12. We say that 15 is ''congruent'' to 3 modulo 12, written 15 ≡ 3 (mod 12), so that 7 + 8 ≡ 3 (mod 12). Similarly, if one starts at 12 and waits 8 hours, the hour hand will be at 8. If one instead waited twice as long, 16 hours, the hour hand would be on 4. This ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Sum Of Two Squares Theorem
In number theory, the sum of two squares theorem relates the prime decomposition of any integer to whether it can be written as a sum of two Square number, squares, such that for some integers , . An integer greater than one can be written as a sum of two squares if and only if its prime decomposition contains no factor , where Prime number, prime p \equiv 3 \pmod 4 and is Parity (mathematics), odd. In writing a number as a sum of two squares, it is allowed for one of the squares to be zero, or for both of them to be equal to each other, so all squares and all doubles of squares are included in the numbers that can be represented in this way. This theorem supplements Fermat's theorem on sums of two squares which says when a prime number can be written as a sum of two squares, in that it also covers the case for composite numbers. A number may have multiple representations as a sum of two squares, counted by the sum of squares function; for instance, every Pythagorean triple a^ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Paley Graph
In mathematics, Paley graphs are undirected graphs constructed from the members of a suitable finite field by connecting pairs of elements that differ by a quadratic residue. The Paley graphs form an infinite family of conference graphs, which yield an infinite family of symmetric conference matrix, conference matrices. Paley graphs allow graph-theoretic tools to be applied to the number theory of quadratic residues, and have interesting properties that make them useful in graph theory more generally. Paley graphs are named after Raymond Paley. They are closely related to the Paley construction for constructing Hadamard matrix, Hadamard matrices from quadratic residues. They were introduced as graphs independently by and . Horst Sachs, Sachs was interested in them for their self-complementarity properties, while Paul Erdős, Erdős and Alfréd Rényi, Rényi studied their symmetries. Paley digraphs are directed graph, directed analogs of Paley graphs that yield antisymmetric conf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Andries Brouwer
Andries Evert Brouwer (born 1951) is a Dutch mathematician and computer programmer, Professor Emeritus at Eindhoven University of Technology (TU/e). He is known as the creator of the greatly expanded 1984 to 1985 versions of the roguelike computer game ''Hack'' that formed the basis for ''NetHack''. He is also a Linux kernel hacker. He is sometimes referred to by the handle ''aeb''. Biography Born in Amsterdam, Brouwer attended the gymnasium, and obtained his MSc in mathematics at the University of Amsterdam in 1971. In 1976 he received his Ph.D. in mathematics from Vrije Universiteit with a thesis entitled "Treelike Spaces and Related Topological Spaces", under the supervision of Maarten Maurice and Pieter Baayen, both of whom were in turn students of Johannes de Groot. In 2004 he received an honorary doctorate from Aalborg University. After graduation Brouwer started his academic career at the Mathematisch Centrum, later Centrum Wiskunde & Informatica. From 1986 to 2012 he w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Algebraic Graph Theory
Algebraic graph theory is a branch of mathematics in which algebraic methods are applied to problems about graphs. This is in contrast to geometric, combinatoric, or algorithmic approaches. There are three main branches of algebraic graph theory, involving the use of linear algebra, the use of group theory, and the study of graph invariants. Branches of algebraic graph theory Using linear algebra The first branch of algebraic graph theory involves the study of graphs in connection with linear algebra. Especially, it studies the spectrum of the adjacency matrix, or the Laplacian matrix of a graph (this part of algebraic graph theory is also called spectral graph theory). For the Petersen graph, for example, the spectrum of the adjacency matrix is (−2, −2, −2, −2, 1, 1, 1, 1, 1, 3). Several theorems relate properties of the spectrum to other graph properties. As a simple example, a connected graph with diameter ''D'' wil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Graph Families
Graph may refer to: Mathematics *Graph (discrete mathematics), a structure made of vertices and edges **Graph theory, the study of such graphs and their properties *Graph (topology), a topological space resembling a graph in the sense of discrete mathematics *Graph of a function *Graph of a relation *Graph paper *Chart, a means of representing data (also called a graph) Computing *Graph (abstract data type), an abstract data type representing relations or connections *graph (Unix), Unix command-line utility *Conceptual graph, a model for knowledge representation and reasoning *Microsoft Graph, a Microsoft API developer platform that connects multiple services and devices Other uses *HMS Graph, HMS ''Graph'', a submarine of the UK Royal Navy See also *Complex network *Graf *Graff (other) *Graph database *Grapheme, in linguistics *Graphemics *Graphic (other) *-graphy (suffix from the Greek for "describe," "write" or "draw") *List of information graphics soft ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |