|
Cn (elliptic Function)
In mathematics, the Jacobi elliptic functions are a set of basic elliptic functions. They are found in the description of the motion of a pendulum, as well as in the design of electronic elliptic filters. While trigonometric functions are defined with reference to a circle, the Jacobi elliptic functions are a generalization which refer to other conic sections, the ellipse in particular. The relation to trigonometric functions is contained in the notation, for example, by the matching notation \operatorname for \sin. The Jacobi elliptic functions are used more often in practical problems than the Weierstrass elliptic functions as they do not require notions of complex analysis to be defined and/or understood. They were introduced by . Carl Friedrich Gauss had already studied special Jacobi elliptic functions in 1797, the lemniscate elliptic functions in particular, but his work was published much later. Overview There are twelve Jacobi elliptic functions denoted by \operatornam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
GitHub
GitHub () is a Proprietary software, proprietary developer platform that allows developers to create, store, manage, and share their code. It uses Git to provide distributed version control and GitHub itself provides access control, bug tracking system, bug tracking, software feature requests, task management, continuous integration, and wikis for every project. Headquartered in California, GitHub, Inc. has been a subsidiary of Microsoft since 2018. It is commonly used to host open source software development projects. GitHub reported having over 100 million developers and more than 420 million Repository (version control), repositories, including at least 28 million public repositories. It is the world's largest source code host Over five billion developer contributions were made to more than 500 million open source projects in 2024. About Founding The development of the GitHub platform began on October 19, 2005. The site was launched in April 2008 by Tom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elliptic Integrals
In integral calculus, an elliptic integral is one of a number of related functions defined as the value of certain integrals, which were first studied by Giulio Fagnano and Leonhard Euler (). Their name originates from their originally arising in connection with the problem of finding the arc length of an ellipse. Modern mathematics defines an "elliptic integral" as any function which can be expressed in the form f(x) = \int_^ R \, dt, where is a rational function of its two arguments, is a polynomial of degree 3 or 4 with no repeated roots, and is a constant. In general, integrals in this form cannot be expressed in terms of elementary functions. Exceptions to this general rule are when has repeated roots, or when contains no odd powers of or if the integral is pseudo-elliptic. However, with the appropriate reduction formula, every elliptic integral can be brought into a form that involves integrals over rational functions and the three Legendre canonical forms, als ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Residue (complex Analysis)
In mathematics, more specifically complex analysis, the residue is a complex number proportional to the contour integral of a meromorphic function along a path enclosing one of its singularities. (More generally, residues can be calculated for any function f\colon \mathbb \setminus \_k \rightarrow \mathbb that is holomorphic except at the discrete points ''k'', even if some of them are essential singularities.) Residues can be computed quite easily and, once known, allow the determination of general contour integrals via the residue theorem. Definition The residue of a meromorphic function f at an isolated singularity a, often denoted \operatorname(f,a), \operatorname_a(f), \mathop_f(z) or \mathop_f(z), is the unique value R such that f(z)- R/(z-a) has an analytic antiderivative in a punctured disk 0<\vert z-a\vert<\delta. Alternatively, residues can be calculated by finding |
Analytic Continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of definition of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where the infinite series representation which initially defined the function becomes divergent. The step-wise continuation technique may, however, come up against difficulties. These may have an essentially topological nature, leading to inconsistencies (defining more than one value). They may alternatively have to do with the presence of singularities. The case of several complex variables is rather different, since singularities then need not be isolated points, and its investigation was a major reason for the development of sheaf cohomology. Initial discussion Suppose ''f'' is an analytic function defined on a non-empty open subset ''U'' of the complex plane If ''V'' is a larger open subset of containing ''U'', and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analytic Function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions. Functions of each type are infinitely differentiable, but complex analytic functions exhibit properties that do not generally hold for real analytic functions. A function is analytic if and only if for every x_0 in its domain, its Taylor series about x_0 converges to the function in some neighborhood of x_0 . This is stronger than merely being infinitely differentiable at x_0 , and therefore having a well-defined Taylor series; the Fabius function provides an example of a function that is infinitely differentiable but not analytic. Definitions Formally, a function f is ''real analytic'' on an open set D in the real line if for any x_0\in D one can write f(x) = \sum_^\infty a_ \left( x-x_0 \right)^ = a_0 + a_1 (x-x_0) + a_2 (x-x_0)^2 + \cdots in which the coefficients a_0, a_1, \dots a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Branch Point
In the mathematical field of complex analysis, a branch point of a multivalued function is a point such that if the function is n-valued (has n values) at that point, all of its neighborhoods contain a point that has more than n values. Multi-valued functions are rigorously studied using Riemann surfaces, and the formal definition of branch points employs this concept. Branch points fall into three broad categories: algebraic branch points, transcendental branch points, and logarithmic branch points. Algebraic branch points most commonly arise from functions in which there is an ambiguity in the extraction of a root, such as solving the equation w^2=z for w as a function of z. Here the branch point is the origin, because the analytic continuation of any solution around a closed loop containing the origin will result in a different function: there is non-trivial monodromy. Despite the algebraic branch point, the function w is well-defined as a multiple-valued function and, in an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multivalued Function
In mathematics, a multivalued function, multiple-valued function, many-valued function, or multifunction, is a function that has two or more values in its range for at least one point in its domain. It is a set-valued function with additional properties depending on context; some authors do not distinguish between set-valued functions and multifunctions, but English Wikipedia currently does, having a separate article for each. A ''multivalued function'' of sets ''f : X → Y'' is a subset : \Gamma_f\ \subseteq \ X\times Y. Write ''f(x)'' for the set of those ''y'' ∈ ''Y'' with (''x,y'') ∈ ''Γf''. If ''f'' is an ordinary function, it is a multivalued function by taking its graph : \Gamma_f\ =\ \. They are called single-valued functions to distinguish them. Motivation The term multivalued function originated in complex analysis, from analytic continuation. It often occurs that one knows the value of a complex analytic function f(z) in some neighbourhood of a point z=a. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elliptic Integral
In integral calculus, an elliptic integral is one of a number of related functions defined as the value of certain integrals, which were first studied by Giulio Fagnano and Leonhard Euler (). Their name originates from their originally arising in connection with the problem of finding the arc length of an ellipse. Modern mathematics defines an "elliptic integral" as any function which can be expressed in the form f(x) = \int_^ R \, dt, where is a rational function of its two arguments, is a polynomial of degree 3 or 4 with no repeated roots, and is a constant. In general, integrals in this form cannot be expressed in terms of elementary functions. Exceptions to this general rule are when has repeated roots, or when contains no odd powers of or if the integral is pseudo-elliptic. However, with the appropriate reduction formula, every elliptic integral can be brought into a form that involves integrals over rational functions and the three Legendre canonical forms, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modell Der Elliptischen Funktion φ=am (u, K) Durch Eine Fläche -Schilling V, 1 - 317-
Modell is the German word for "model" and also a surname. It may refer to: People * Arnold Modell (1924–2022), American professor of social psychiatry * Art Modell Arthur Bertram Modell (June 23, 1925 – September 6, 2012) was an American businessman, entrepreneur and National Football League (NFL) team owner. He owned the Cleveland Browns franchise for 35 years and established the Baltimore Ravens f ... (1925–2012), American business executive and sports team owner * Bernadette Modell, (born 1935), British geneticist * David Modell (1961–2017), American business executive and sports team owner * Frank Modell (1917-2016), American cartoonist * Merriam Modell (1908–1994), American author of pulp fiction * Pat Modell (1931–2011), American TV actress * Rod Modell, given name for Deepchord, electronic music producer from Detroit, Michigan * William Modell (1921–2008), American businessman and chairman of Modell's Sporting Goods Companies * Modell's Sportin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
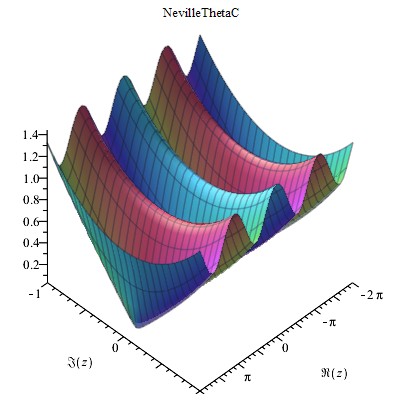
Neville Theta Function
In mathematics, the Neville theta functions, named after Eric Harold Neville, are defined as follows: : \theta_c(z,m)=\frac \,\, \sum _^\infty (q(m))^ \cos \left(\frac \right) : \theta_d(z,m)=\frac\,\,\left( 1+2\,\sum _^\infty (q(m))^ \cos \left( \frac \right) \right) : \theta_n(z, m) =\frac \,\,\left( 1+2\sum _^\infty (-1)^k (q(m))^ \cos \left(\frac \right) \right) : \theta_s(z, m)=\frac\,\, \sum_^\infty (-1)^k (q(m))^ \sin\left(\frac \right) where: ''K(m)'' is the complete elliptic integral of the first kind, K'(m)=K(1-m), and q(m)=e^ is the elliptic nome. Note that the functions ''θp(z,m)'' are sometimes defined in terms of the nome ''q(m)'' and written ''θp(z,q)'' (e.g. NIST). The functions may also be written in terms of the ''τ'' parameter ''θp(z, τ)'' where q=e^. Relationship to other functions The Neville theta functions may be expressed in terms of the Jacobi theta functions :\theta_s(z, \tau)=\theta_3^2(0, \tau)\theta_1(z', ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |