|
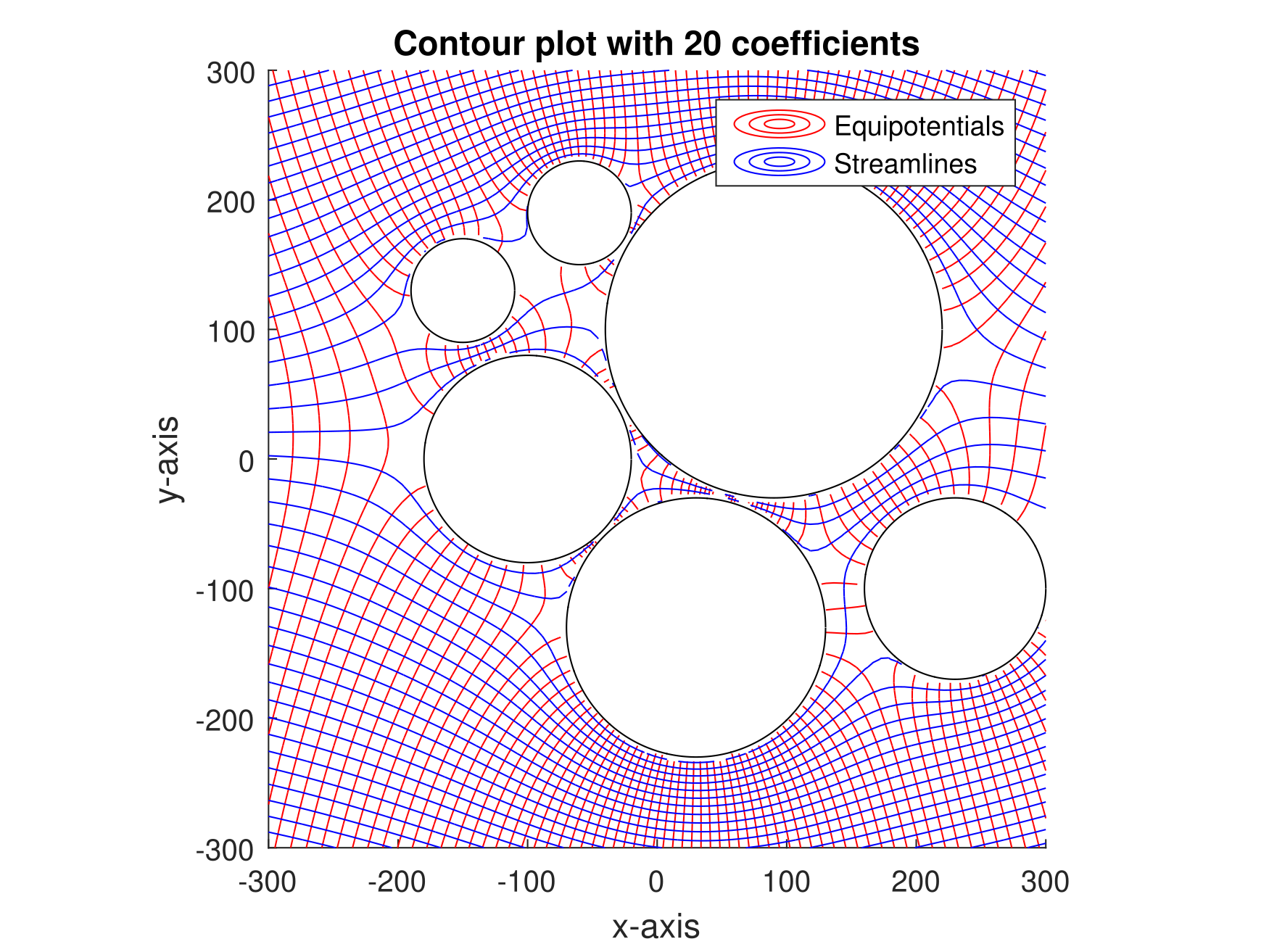
Analytic Element Method
The analytic element method (AEM) is a numerical method used for the solution of partial differential equations. It was initially developed by O.D.L. Strack at the University of Minnesota. It is similar in nature to the boundary element method (BEM), as it does not rely upon the discretization of volumes or areas in the modeled system; only internal and external boundaries are discretized. One of the primary distinctions between AEM and BEMs is that the boundary integrals are calculated analytically. Although originally developed to model groundwater flow, AEM has subsequently been applied to other fields of study including studies of heat flow and conduction, periodic waves, and deformation by force. Mathematical basis The basic premise of the analytic element method is that, for linear differential equations, elementary solutions may be superimposed to obtain more complex solutions. A suite of 2D and 3D analytic solutions ("elements") are available for different governing equ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Numerical Analysis
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic computation, symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods that attempt to find approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences like economics, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics (predicting the motions of planets, stars and galaxies), numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Conformal Map
In mathematics, a conformal map is a function (mathematics), function that locally preserves angles, but not necessarily lengths. More formally, let U and V be open subsets of \mathbb^n. A function f:U\to V is called conformal (or angle-preserving) at a point u_0\in U if it preserves angles between directed curves through u_0, as well as preserving orientation. Conformal maps preserve both angles and the shapes of infinitesimally small figures, but not necessarily their size or curvature. The conformal property may be described in terms of the Jacobian matrix and determinant, Jacobian derivative matrix of a coordinate transformation. The transformation is conformal whenever the Jacobian at each point is a positive scalar times a rotation matrix (Orthogonal matrix, orthogonal with determinant one). Some authors define conformality to include orientation-reversing mappings whose Jacobians can be written as any scalar times any orthogonal matrix. For mappings in two dimensions, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Henk M
Henk is a Dutch male given name, originally a short form of Hendrik. It influenced " Hank" which is used in English-speaking countries (mainly in the US) as a form of "Henry". Academics *Henk Aertsen (born 1943), Dutch Anglo-Saxon linguist *Henk Barendregt (born 1947), Dutch logician *Henk Jaap Beentje (born 1951), Dutch botanist *Henk Blezer (born 1961), Dutch Tibetologist, Indologist, and scholar of Buddhist studies *Henk Bodewitz (1939–2022), Dutch Sanskrit scholar *Henk J. M. Bos (born 1940), Dutch historian of mathematics *Henk Braakhuis (born 1939), Dutch historian of philosophy *Henk Buck (1930–2023), Dutch organic chemist * Henk van Dongen (1936–2011), Dutch organizational theorist and policy advisor * Henk Dorgelo (1894–1961), Dutch physicist and academic *Henk van der Flier (born 1945), Dutch psychologist * Henk A. M. J. ten Have (born 1951), Dutch medical ethicist * Henk van de Hulst (1918–2000), Dutch astronomer and mathematician * Henk Lombaers (1920–2007 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Superposition Principle
The superposition principle, also known as superposition property, states that, for all linear systems, the net response caused by two or more stimuli is the sum of the responses that would have been caused by each stimulus individually. So that if input ''A'' produces response ''X'', and input ''B'' produces response ''Y'', then input (''A'' + ''B'') produces response (''X'' + ''Y''). A function F(x) that satisfies the superposition principle is called a linear function. Superposition can be defined by two simpler properties: additivity F(x_1 + x_2) = F(x_1) + F(x_2) and homogeneity F(ax) = a F(x) for scalar . This principle has many applications in physics and engineering because many physical systems can be modeled as linear systems. For example, a beam can be modeled as a linear system where the input stimulus is the load on the beam and the output response is the deflection of the beam. The importance of linear systems is that they are easier to analyze mathemat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Conformal Map
In mathematics, a conformal map is a function (mathematics), function that locally preserves angles, but not necessarily lengths. More formally, let U and V be open subsets of \mathbb^n. A function f:U\to V is called conformal (or angle-preserving) at a point u_0\in U if it preserves angles between directed curves through u_0, as well as preserving orientation. Conformal maps preserve both angles and the shapes of infinitesimally small figures, but not necessarily their size or curvature. The conformal property may be described in terms of the Jacobian matrix and determinant, Jacobian derivative matrix of a coordinate transformation. The transformation is conformal whenever the Jacobian at each point is a positive scalar times a rotation matrix (Orthogonal matrix, orthogonal with determinant one). Some authors define conformality to include orientation-reversing mappings whose Jacobians can be written as any scalar times any orthogonal matrix. For mappings in two dimensions, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Boundary Element Method
The boundary element method (BEM) is a numerical computational method of solving linear partial differential equations which have been formulated as integral equations (i.e. in ''boundary integral'' form), including fluid mechanics, acoustics, electromagnetics (where the technique is known as method of moments or abbreviated as MoM), fracture mechanics, and contact mechanics. Mathematical basis The integral equation may be regarded as an exact solution of the governing partial differential equation. The boundary element method attempts to use the given boundary conditions to fit boundary values into the integral equation, rather than values throughout the space defined by a partial differential equation. Once this is done, in the post-processing stage, the integral equation can then be used again to calculate numerically the solution directly at any desired point in the interior of the solution domain. BEM is applicable to problems for which Green's functions can be calculated. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Finite Difference Method
In numerical analysis, finite-difference methods (FDM) are a class of numerical techniques for solving differential equations by approximating Derivative, derivatives with Finite difference approximation, finite differences. Both the spatial domain and time domain (if applicable) are Discretization, discretized, or broken into a finite number of intervals, and the values of the solution at the end points of the intervals are approximated by solving algebraic equations containing finite differences and values from nearby points. Finite difference methods convert ordinary differential equations (ODE) or partial differential equations (PDE), which may be Nonlinear partial differential equation, nonlinear, into a system of linear equations that can be solved by matrix algebra techniques. Modern computers can perform these linear algebra computations efficiently, and this, along with their relative ease of implementation, has led to the widespread use of FDM in modern numerical analysi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Finite Element Method
Finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat transfer, fluid flow, mass transport, and electromagnetic potential. Computers are usually used to perform the calculations required. With high-speed supercomputers, better solutions can be achieved and are often required to solve the largest and most complex problems. FEM is a general numerical method for solving partial differential equations in two- or three-space variables (i.e., some boundary value problems). There are also studies about using FEM to solve high-dimensional problems. To solve a problem, FEM subdivides a large system into smaller, simpler parts called finite elements. This is achieved by a particular space discretization in the space dimensions, which is implemented by the construction of a mesh of the object: the numer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Stream Function
In fluid dynamics, two types of stream function (or streamfunction) are defined: * The two-dimensional (or Lagrange) stream function, introduced by Joseph Louis Lagrange in 1781, is defined for incompressible flow, incompressible (divergence-free), two-dimensional fluid flow, flows. * The Stokes stream function, named after George Gabriel Stokes, is defined for incompressible, three-dimensional flows with axisymmetry. The properties of stream functions make them useful for analyzing and graphically illustrating flows. The remainder of this article describes the two-dimensional stream function. Two-dimensional stream function Assumptions The two-dimensional stream function is based on the following assumptions: * The flow field can be described as two-dimensional plane flow, with velocity vector : \quad \mathbf = \begin u (x,y,t) \\ v (x,y,t) \\ 0 \end. * The velocity satisfies the continuity equation for incompressible flow: : \quad \nabla \cdot \mathbf = 0. * The domain h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Groundwater Discharge
Groundwater discharge is the volumetric flow rate of groundwater through an aquifer. Total groundwater discharge, as reported through a specified area, is similarly expressed as: :Q = \fracKA where :''Q'' is the total groundwater discharge ( 3·T−1 m3/s), :''K'' is the hydraulic conductivity of the aquifer ( ·T−1 m/s), :''dh/dl'' is the hydraulic gradient ( ·L−1 unitless), and :''A'' is the area which the groundwater is flowing through ( 2 m2) For example, this can be used to determine the flow rate of water flowing along a plane with known geometry. The discharge potential The discharge potential is a potential in groundwater mechanics which links the physical properties, hydraulic head, with a mathematical formulation for the energy as a function of position. The discharge potential, \Phi 3·T−1 is defined in such way that its gradient equals the discharge vector. Q_x = -\frac Q_y = -\frac Thus the hydraulic head may be calculated in terms of the discharge pote ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Unit Circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Euclidean plane. In topology, it is often denoted as because it is a one-dimensional unit -sphere. If is a point on the unit circle's circumference, then and are the lengths of the legs of a right triangle whose hypotenuse has length 1. Thus, by the Pythagorean theorem, and satisfy the equation x^2 + y^2 = 1. Since for all , and since the reflection of any point on the unit circle about the - or -axis is also on the unit circle, the above equation holds for all points on the unit circle, not only those in the first quadrant. The interior of the unit circle is called the open unit disk, while the interior of the unit circle combined with the unit circle itself is called the closed unit disk. One may also use other notions of "dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Biharmonic Equation
In mathematics, the biharmonic equation is a fourth-order partial differential equation which arises in areas of continuum mechanics, including linear elasticity theory and the solution of Stokes flows. Specifically, it is used in the modeling of thin structures that react Elasticity (physics), elastically to external forces. Notation It is written as \nabla^4 \varphi = 0 or \nabla^2 \nabla^2 \varphi = 0 or \Delta^2 \varphi = 0 where \nabla^4, which is the fourth power of the del operator and the square of the Laplacian operator \nabla^2 (or \Delta), is known as the biharmonic operator or the bilaplacian operator. In Cartesian coordinates, it can be written in n dimensions as: \nabla^4 \varphi = \sum_^n\sum_^n \partial_i\partial_i\partial_j\partial_j \varphi = \left(\sum_^n \partial_i\partial_i\right) \left(\sum_^n \partial_j\partial_j\right) \varphi. Because the formula here contains a summation of indices, many mathematicians prefer the notation \Delta^2 over \nabla^4 because ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |