|
XOR Swap Algorithm
In computer programming, the exclusive or swap (sometimes shortened to XOR swap) is an algorithm that uses the exclusive or bitwise operation to swap the values of two variables without using the temporary variable which is normally required. The algorithm is primarily a novelty and a way of demonstrating properties of the ''exclusive or'' operation. It is sometimes discussed as a program optimization, but there are almost no cases where swapping via ''exclusive or'' provides benefit over the standard, obvious technique. The algorithm Conventional swapping requires the use of a temporary storage variable. Using the XOR swap algorithm, however, no temporary storage is needed. The algorithm is as follows: X := Y XOR X; // XOR the values and store the result in X Y := X XOR Y; // XOR the values and store the result in Y X := Y XOR X; // XOR the values and store the result in X Since XOR is a commutative operation, either X XOR Y or Y XOR X can be used interchangeably in any of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
XOR Swap
Exclusive or, exclusive disjunction, exclusive alternation, logical non-equivalence, or logical inequality is a logical operator whose negation is the logical biconditional. With two inputs, XOR is true if and only if the inputs differ (one is true, one is false). With multiple inputs, XOR is true if and only if the number of true inputs is odd. It gains the name "exclusive or" because the meaning of "or" is ambiguous when both operands are true. XOR ''excludes'' that case. Some informal ways of describing XOR are "one or the other but not both", "either one or the other", and "A or B, but not A and B". It is symbolized by the prefix operator J Translated as and by the infix operators XOR (, , or ), EOR, EXOR, \dot, \overline, \underline, , \oplus, \nleftrightarrow, and \not\equiv. Definition The truth table of A\nleftrightarrow B shows that it outputs true whenever the inputs differ: Equivalences, elimination, and introduction Exclusive disjunction essentially mea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Associativity
In mathematics, the associative property is a property of some binary operations that rearranging the parentheses in an expression will not change the result. In propositional logic, associativity is a Validity (logic), valid rule of replacement for well-formed formula, expressions in Formal proof, logical proofs. Within an expression containing two or more occurrences in a row of the same associative operator, the order in which the Operation (mathematics), operations are performed does not matter as long as the sequence of the operands is not changed. That is (after rewriting the expression with parentheses and in infix notation if necessary), rearranging the parentheses in such an expression will not change its value. Consider the following equations: \begin (2 + 3) + 4 &= 2 + (3 + 4) = 9 \,\\ 2 \times (3 \times 4) &= (2 \times 3) \times 4 = 24 . \end Even though the parentheses were rearranged on each line, the values of the expressions were not altered. Since this holds ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aliasing (computing)
In computing, aliasing describes a situation in which a data location in memory can be accessed through different symbolic names in the program. Thus, modifying the data through one name implicitly modifies the values associated with all aliased names, which may not be expected by the programmer. As a result, aliasing makes it particularly difficult to understand, analyze and optimize programs. Aliasing analysers intend to make and compute useful information for understanding aliasing in programs. Aliased pointers Aliasing can occur in any language that can refer to one location in memory with more than one name (for example, with pointers). This is a common problem with functions that accept pointer arguments, and their tolerance (or the lack thereof) for aliasing must be carefully documented, particularly for functions that perform complex manipulations on memory areas passed to them. Specified aliasing Controlled aliasing behaviour may be desirable in some cases (that is, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Instruction-level Parallelism
Instruction-level parallelism (ILP) is the Parallel computing, parallel or simultaneous execution of a sequence of Instruction set, instructions in a computer program. More specifically, ILP refers to the average number of instructions run per step of this parallel execution. Discussion ILP must not be confused with Concurrency (computer science), concurrency. In ILP, there is a single specific Thread (computing), thread of execution of a Process (computing), process. On the other hand, concurrency involves the assignment of multiple threads to a Central processing unit, CPU's core in a strict alternation, or in true parallelism if there are enough CPU cores, ideally one core for each runnable thread. There are two approaches to instruction-level parallelism: Computer hardware, hardware and software. Hardware-level ILP works upon dynamic parallelism, whereas software-level ILP works on static parallelism. Dynamic parallelism means that the processor decides at run time whic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Instruction Pipeline
In computer engineering, instruction pipelining is a technique for implementing instruction-level parallelism within a single processor. Pipelining attempts to keep every part of the processor busy with some instruction by dividing incoming Machine code, instructions into a series of sequential steps (the eponymous "Pipeline (computing), pipeline") performed by different Central processing unit#Structure and implementation, processor units with different parts of instructions processed in parallel. Concept and motivation In a pipelined computer, instructions flow through the central processing unit (CPU) in stages. For example, it might have one stage for each step of the von Neumann architecture, von Neumann cycle: Fetch the instruction, fetch the operands, do the instruction, write the results. A pipelined computer usually has "pipeline registers" after each stage. These store information from the instruction and calculations so that the logic gates of the next stage can do th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
CPU Architecture
In computer science and computer engineering, computer architecture is a description of the structure of a computer system made from component parts. It can sometimes be a high-level description that ignores details of the implementation. At a more detailed level, the description may include the instruction set architecture design, microarchitecture design, logic design, and implementation. History The first documented computer architecture was in the correspondence between Charles Babbage and Ada Lovelace, describing the analytical engine. While building the computer Z1 in 1936, Konrad Zuse described in two patent applications for his future projects that machine instructions could be stored in the same storage used for data, i.e., the stored-program concept. Two other early and important examples are: * John von Neumann's 1945 paper, First Draft of a Report on the EDVAC, which described an organization of logical elements; and *Alan Turing's more detailed ''Proposed Electr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Guard (computer Science)
In computer programming, a guard is a Boolean expression that must evaluate to true if the execution of the program is to continue in the branch in question. Regardless of which programming language is used, a guard clause, guard code, or guard statement is a check of integrity preconditions used to avoid errors during execution. The term guard clause is a Software design pattern attributed to Kent Beck who codified many often unnamed coding practices into named software design patterns, the practice of using this technique dates back to at least the early 1960's. The guard clause most commonly is added at the beginning of a procedure and is said to "guard" the rest of the procedure by handling edgecases upfront. Uses A typical example is checking that a reference about to be processed is not null, which avoids null-pointer failures. Other uses include using a Boolean field for idempotence (so subsequent calls are nops), as in the dispose pattern. public String foo(Str ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
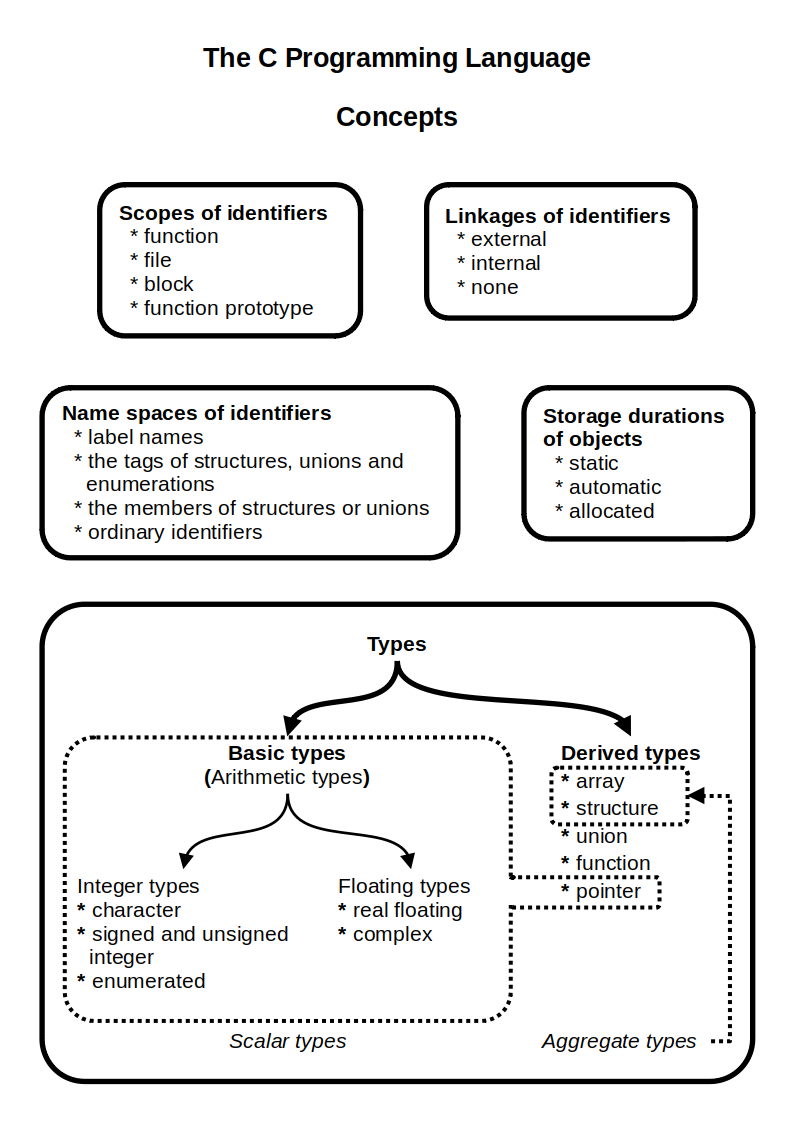
C (programming Language)
C (''pronounced'' '' – like the letter c'') is a general-purpose programming language. It was created in the 1970s by Dennis Ritchie and remains very widely used and influential. By design, C's features cleanly reflect the capabilities of the targeted Central processing unit, CPUs. It has found lasting use in operating systems code (especially in Kernel (operating system), kernels), device drivers, and protocol stacks, but its use in application software has been decreasing. C is commonly used on computer architectures that range from the largest supercomputers to the smallest microcontrollers and embedded systems. A successor to the programming language B (programming language), B, C was originally developed at Bell Labs by Ritchie between 1972 and 1973 to construct utilities running on Unix. It was applied to re-implementing the kernel of the Unix operating system. During the 1980s, C gradually gained popularity. It has become one of the most widely used programming langu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Block Matrices
In mathematics, a block matrix or a partitioned matrix is a matrix that is interpreted as having been broken into sections called blocks or submatrices. Intuitively, a matrix interpreted as a block matrix can be visualized as the original matrix with a collection of horizontal and vertical lines, which break it up, or partition it, into a collection of smaller matrices. For example, the 3x4 matrix presented below is divided by horizontal and vertical lines into four blocks: the top-left 2x3 block, the top-right 2x1 block, the bottom-left 1x3 block, and the bottom-right 1x1 block. : \left \begin a_ & a_ & a_ & b_ \\ a_ & a_ & a_ & b_ \\ \hline c_ & c_ & c_ & d \end \right Any matrix may be interpreted as a block matrix in one or more ways, with each interpretation defined by how its rows and columns are partitioned. This notion can be made more precise for an n by m matrix M by partitioning n into a collection \text, and then partitioning m into a collection \text. The original m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shear Mapping
In plane geometry, a shear mapping is an affine transformation that displaces each point in a fixed direction by an amount proportional to its signed distance function, signed distance from a given straight line, line parallel (geometry), parallel to that direction. This type of mapping is also called shear transformation, transvection, or just shearing. The transformations can be applied with a shear matrix or transvection, an elementary matrix that represents the Elementary row operations#Row-addition transformations, addition of a multiple of one row or column to another. Such a matrix (mathematics), matrix may be derived by taking the identity matrix and replacing one of the zero elements with a non-zero value. An example is the linear map that takes any point with Cartesian coordinates, coordinates (x,y) to the point (x + 2y,y). In this case, the displacement is horizontal by a factor of 2 where the fixed line is the -axis, and the signed distance is the -coordinate. Not ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elementary Matrix
In mathematics, an elementary matrix is a square matrix obtained from the application of a single elementary row operation to the identity matrix. The elementary matrices generate the general linear group when is a field. Left multiplication (pre-multiplication) by an elementary matrix represents elementary row operations, while right multiplication (post-multiplication) represents elementary column operations. Elementary row operations are used in Gaussian elimination to reduce a matrix to row echelon form. They are also used in Gauss–Jordan elimination to further reduce the matrix to reduced row echelon form. Elementary row operations There are three types of elementary matrices, which correspond to three types of row operations (respectively, column operations): ;Row switching: A row within the matrix can be switched with another row. : R_i \leftrightarrow R_j ;Row multiplication: Each element in a row can be multiplied by a non-zero constant. It is also known as ''sca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Field With Two Elements
(also denoted \mathbb F_2, or \mathbb Z/2\mathbb Z) is the finite field with two elements. is the Field (mathematics), field with the smallest possible number of elements, and is unique if the additive identity and the multiplicative identity are denoted respectively and , as usual. The elements of may be identified with the two possible values of a bit and to the Boolean domain, Boolean values ''true'' and ''false''. It follows that is fundamental and ubiquitous in computer science and its mathematical logic, logical foundations. Definition GF(2) is the unique field with two elements with its additive identity, additive and multiplicative identity, multiplicative identities respectively denoted and . Its addition is defined as the usual addition of integers but modulo 2 and corresponds to the table below: If the elements of GF(2) are seen as Boolean values, then the addition is the same as that of the logical XOR operation. Since each element equals its opposite (m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |