|
Weyl Character Formula
In mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by . There is a closely related formula for the character of an irreducible representation of a semisimple Lie algebra. In Weyl's approach to the representation theory of connected compact Lie groups, the proof of the character formula is a key step in proving that every dominant integral element actually arises as the highest weight of some irreducible representation. Important consequences of the character formula are the Weyl dimension formula and the Kostant multiplicity formula. By definition, the character \chi of a representation \pi of ''G'' is the trace of \pi(g), as a function of a group element g\in G. The irreducible representations in this case are all finite-dimensional (this is part of the Peter–Weyl theorem); so the notion of trace is the usual one from linear algeb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kostant Partition Function
In representation theory, a branch of mathematics, the Kostant partition function, introduced by , of a root system \Delta is the number of ways one can represent a vector (weight) as a non-negative integer linear combination of the positive roots \Delta^+\subset\Delta. Kostant used it to rewrite the Weyl character formula as a formula (the Kostant multiplicity formula) for the multiplicity of a weight of an irreducible representation of a semisimple Lie algebra. An alternative formula, that is more computationally efficient in some cases, is Freudenthal's formula. The Kostant partition function can also be defined for Kac–Moody algebras and has similar properties. Examples A2 Consider the A2 root system, with positive roots \alpha_1, \alpha_2, and \alpha_3:=\alpha_1+\alpha_2. If an element \mu can be expressed as a non-negative integer linear combination of \alpha_1, \alpha_2, and \alpha_3, then since \alpha_3=\alpha_1+\alpha_2, it can also be expressed as a non-negative ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hans Freudenthal
Hans Freudenthal (17 September 1905 – 13 October 1990) was a Jewish-German, Jewish German-born Netherlands, Dutch mathematician. He made substantial contributions to algebraic topology and also took an interest in literature, philosophy, history and mathematics education. Biography Freudenthal was born in Luckenwalde, Province of Brandenburg, Brandenburg, on 17 September 1905, the son of a Jewish teacher. He was interested in both mathematics and literature as a child, and studied mathematics at the Humboldt University of Berlin, University of Berlin beginning in 1923.. He met L. E. J. Brouwer in 1927, when Brouwer came to Berlin to give a lecture, and in the same year Freudenthal also visited the University of Paris.. He completed his thesis work with Heinz Hopf at Berlin, defended a thesis on the End (topology), ends of topological groups in 1930, and was officially awarded a degree in October 1931. After defending his thesis in 1930, he moved to Amsterdam to take up a positio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
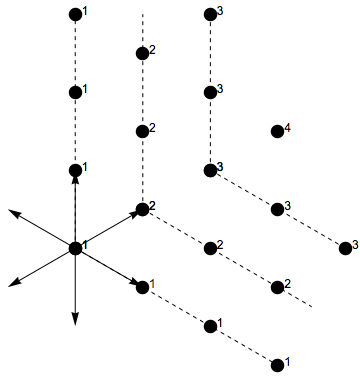
Positive Root
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras, especially the classification and representation theory of semisimple Lie algebras. Since Lie groups (and some analogues such as algebraic groups) and Lie algebras have become important in many parts of mathematics during the twentieth century, the apparently special nature of root systems belies the number of areas in which they are applied. Further, the classification scheme for root systems, by Dynkin diagrams, occurs in parts of mathematics with no overt connection to Lie theory (such as singularity theory). Finally, root systems are important for their own sake, as in spectral graph theory. Definitions and examples As a first example, consider the six vectors in 2-dimensional Euclidean space, R2, as shown in the image at the right; call them roots. These vectors span the whole ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Affine Lie Algebra
In mathematics, an affine Lie algebra is an infinite-dimensional Lie algebra that is constructed in a canonical fashion out of a finite-dimensional simple Lie algebra. Given an affine Lie algebra, one can also form the associated affine Kac-Moody algebra, as described below. From a purely mathematical point of view, affine Lie algebras are interesting because their representation theory, like representation theory of finite-dimensional semisimple Lie algebras, is much better understood than that of general Kac–Moody algebras. As observed by Victor Kac, the character formula for representations of affine Lie algebras implies certain combinatorial identities, the Macdonald identities. Affine Lie algebras play an important role in string theory and two-dimensional conformal field theory due to the way they are constructed: starting from a simple Lie algebra \mathfrak, one considers the loop algebra, L\mathfrak, formed by the \mathfrak-valued functions on a circle (interpreted as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Macdonald Identities
In mathematics Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ..., the Macdonald identities are some infinite product identities associated to affine root systems, introduced by . They include as special cases the Jacobi triple product identity, Watson's quintuple product identity, several identities found by , and a 10-fold product identity found by . and pointed out that the Macdonald identities are the analogs of the Weyl denominator formula for affine Kac–Moody algebras and superalgebras. References * * * * * *{{Citation , last1=Winquist , first1=Lasse , title=An elementary proof of p(11m+6) ≡ 0 mod 11 , mr=0236136 , year=1969 , journal=Journal of Combinatorial Theory , volume=6 , pages=56–59 , doi=10.1016/s0021-9800(69)80105-5, doi-access=free Lie al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kac–Moody Algebra
In mathematics, a Kac–Moody algebra (named for Victor Kac and Robert Moody, who independently and simultaneously discovered them in 1968) is a Lie algebra, usually infinite-dimensional, that can be defined by generators and relations through a generalized Cartan matrix. These algebras form a generalization of finite-dimensional semisimple Lie algebras, and many properties related to the structure of a Lie algebra such as its root system, irreducible representations, and connection to flag manifolds have natural analogues in the Kac–Moody setting. A class of Kac–Moody algebras called affine Lie algebras is of particular importance in mathematics and theoretical physics, especially two-dimensional conformal field theory and the theory of exactly solvable models. Kac discovered an elegant proof of certain combinatorial identities, the Macdonald identities, which is based on the representation theory of affine Kac–Moody algebras. Howard Garland and James Lepowsky demonstrated ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Highest-weight Representation
In the mathematical field of representation theory, a weight of an algebra ''A'' over a field F is an algebra homomorphism from ''A'' to F, or equivalently, a one-dimensional representation of ''A'' over F. It is the algebra analogue of a multiplicative character of a group. The importance of the concept, however, stems from its application to representations of Lie algebras and hence also to representations of algebraic and Lie groups. In this context, a weight of a representation is a generalization of the notion of an eigenvalue, and the corresponding eigenspace is called a weight space. Motivation and general concept Given a set ''S'' of n \times n matrices over the same field, each of which is diagonalizable, and any two of which commute, it is always possible to simultaneously diagonalize all of the elements of ''S''.In fact, given a set of commuting matrices over an algebraically closed field, they are simultaneously triangularizable, without needing to assume that th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Casimir Element
In mathematics, a Casimir element (also known as a Casimir invariant or Casimir operator) is a distinguished element of the center of the universal enveloping algebra of a Lie algebra. A prototypical example is the squared angular momentum operator, which is a Casimir element of the three-dimensional rotation group. More generally, Casimir elements can be used to refer to ''any'' element of the center of the universal enveloping algebra. The algebra of these elements is known to be isomorphic to a polynomial algebra through the Harish-Chandra isomorphism. The Casimir element is named after Hendrik Casimir, who identified them in his description of rigid body dynamics in 1931. Definition The most commonly-used Casimir invariant is the quadratic invariant. It is the simplest to define, and so is given first. However, one may also have Casimir invariants of higher order, which correspond to homogeneous symmetric polynomials of higher order. Quadratic Casimir element Supp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lie Algebra Representation
In the mathematical field of representation theory, a Lie algebra representation or representation of a Lie algebra is a way of writing a Lie algebra as a set of matrices (or endomorphisms of a vector space) in such a way that the Lie bracket is given by the commutator. In the language of physics, one looks for a vector space V together with a collection of operators on V satisfying some fixed set of commutation relations, such as the relations satisfied by the angular momentum operators. The notion is closely related to that of a representation of a Lie group. Roughly speaking, the representations of Lie algebras are the differentiated form of representations of Lie groups, while the representations of the universal cover of a Lie group are the integrated form of the representations of its Lie algebra. In the study of representations of a Lie algebra, a particular ring, called the universal enveloping algebra, associated with the Lie algebra plays an important role. The u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
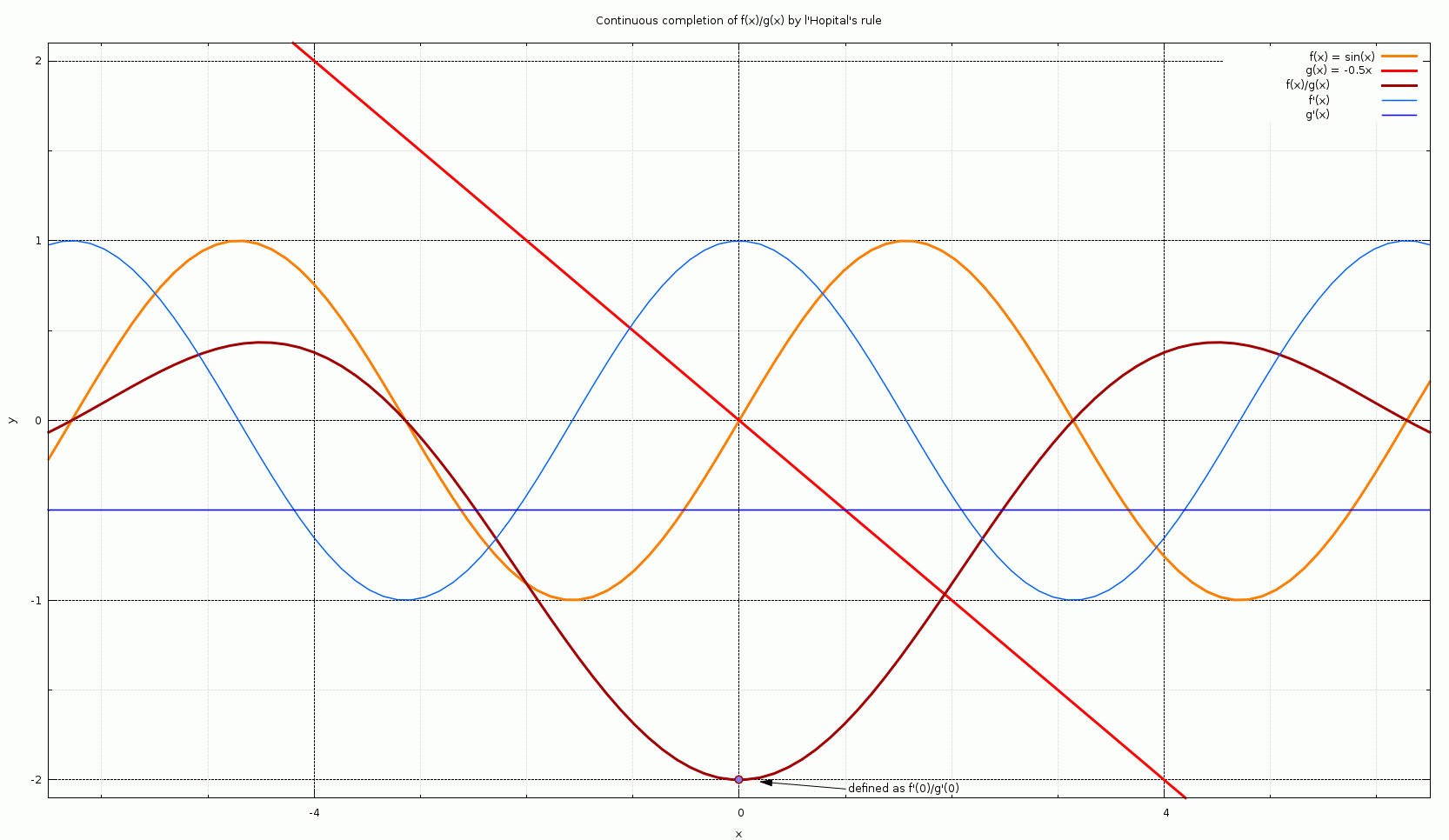
L'Hôpital's Rule
L'Hôpital's rule (, ), also known as Bernoulli's rule, is a mathematical theorem that allows evaluating limits of indeterminate forms using derivatives. Application (or repeated application) of the rule often converts an indeterminate form to an expression that can be easily evaluated by substitution. The rule is named after the 17th-century French mathematician Guillaume de l'Hôpital. Although the rule is often attributed to de l'Hôpital, the theorem was first introduced to him in 1694 by the Swiss mathematician Johann Bernoulli. L'Hôpital's rule states that for functions and which are defined on an open interval and differentiable on I\setminus \ for a (possibly infinite) accumulation point of , if \lim \limits_f(x)=\lim \limits_g(x)=0 \text\pm\infty, and g'(x)\ne 0 for all in I\setminus \, and \lim \limits_\frac exists, then :\lim_\frac = \lim_\frac. The differentiation of the numerator and denominator often simplifies the quotient or converts it to a limit t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vandermonde Determinant
In algebra, the Vandermonde polynomial of an ordered set of ''n'' variables X_1,\dots, X_n, named after Alexandre-Théophile Vandermonde, is the polynomial: :V_n = \prod_ (X_j-X_i). (Some sources use the opposite order (X_i-X_j), which changes the sign \binom times: thus in some dimensions the two formulas agree in sign, while in others they have opposite signs.) It is also called the Vandermonde determinant, as it is the determinant of the Vandermonde matrix. The value depends on the order of the terms: it is an alternating polynomial, not a symmetric polynomial. Alternating The defining property of the Vandermonde polynomial is that it is ''alternating'' in the entries, meaning that permuting the X_i by an odd permutation changes the sign, while permuting them by an even permutation does not change the value of the polynomial – in fact, it is the basic alternating polynomial, as will be made precise below. It thus depends on the order, and is zero if two entries are equa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |