|
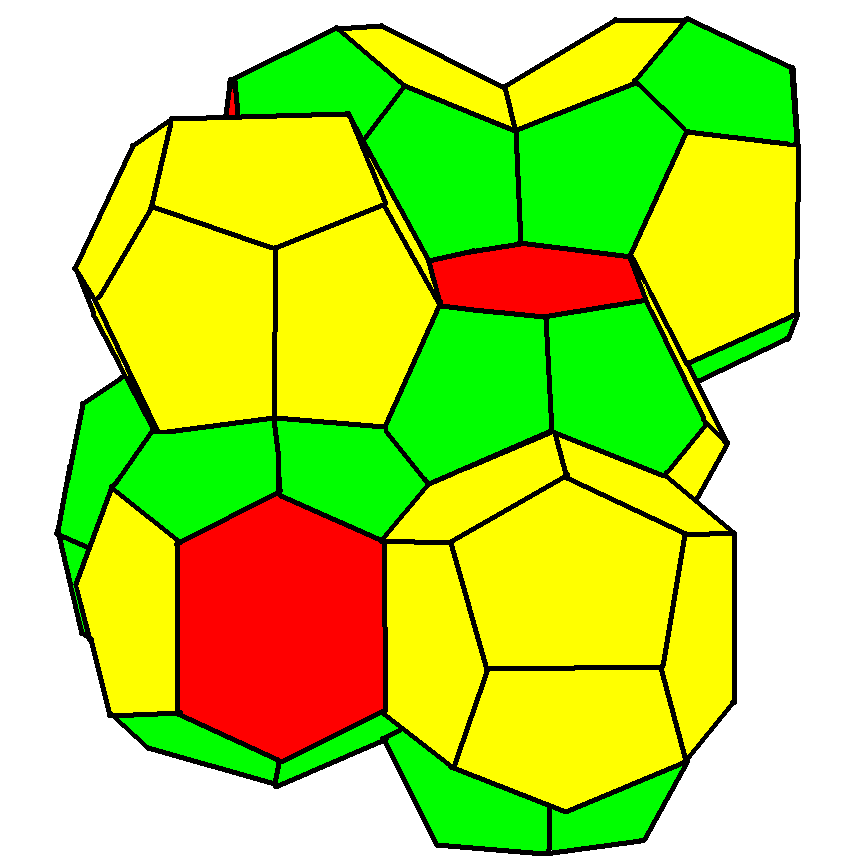
Weaire–Phelan Structure
In geometry, the Weaire–Phelan structure is a three-dimensional structure representing an idealised foam of equal-sized bubbles, with two different shapes. In 1993, Denis Weaire and Robert Phelan found that this structure was a better solution of the Kelvin problem of tiling space by equal volume cells of minimum surface area than the previous best-known solution, the Kelvin structure. History and the Kelvin problem In two dimensions, the subdivision of the plane into cells of equal area with minimum average perimeter is given by the hexagonal tiling, but although the first record of this honeycomb conjecture goes back to the ancient Roman scholar Marcus Terentius Varro, it was not proven until the work of Thomas C. Hales in 1999. In 1887, Lord Kelvin asked the corresponding question for three-dimensional space: how can space be partitioned into cells of equal volume with the least area of surface between them? Or, in short, what was the most efficient soap bubble foam? Thi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
12-14-hedral Honeycomb
1 (one, unit, unity) is a number representing a single or the only entity. 1 is also a numerical digit and represents a single unit of counting or measurement. For example, a line segment of ''unit length'' is a line segment of length 1. In conventions of sign where zero is considered neither positive nor negative, 1 is the first and smallest positive integer. It is also sometimes considered the first of the infinite sequence of natural numbers, followed by 2, although by other definitions 1 is the second natural number, following 0. The fundamental mathematical property of 1 is to be a multiplicative identity, meaning that any number multiplied by 1 equals the same number. Most if not all properties of 1 can be deduced from this. In advanced mathematics, a multiplicative identity is often denoted 1, even if it is not a number. 1 is by convention not considered a prime number; this was not universally accepted until the mid-20th century. Additionally, 1 is th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cubic Crystal System
In crystallography, the cubic (or isometric) crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals. There are three main varieties of these crystals: *Primitive cubic (abbreviated ''cP'' and alternatively called simple cubic) *Body-centered cubic (abbreviated ''cI'' or bcc) *Face-centered cubic (abbreviated ''cF'' or fcc, and alternatively called ''cubic close-packed'' or ccp) Each is subdivided into other variants listed below. Although the ''unit cells'' in these crystals are conventionally taken to be cubes, the primitive unit cells often are not. Bravais lattices The three Bravais lattices in the cubic crystal system are: The primitive cubic lattice (cP) consists of one lattice point on each corner of the cube; this means each simple cubic unit cell has in total one lattice point. Each atom at a lattice point is then shared equally between eight adjacent c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fibrifold Notation
In mathematics, a fibrifold is (roughly) a fiber space whose fibers and base spaces are orbifolds. They were introduced by , who introduced a system of notation for 3-dimensional fibrifolds and used this to assign names to the 219 affine space group types. 184 of these are considered reducible, and 35 irreducible. Irreducible cubic space groups The 35 irreducible space groups correspond to the cubic space group. Irreducible group symbols (indexed 195−230) in Hermann–Mauguin notation In geometry, Hermann–Mauguin notation is used to represent the symmetry elements in point groups, plane groups and space groups. It is named after the German crystallographer Carl Hermann (who introduced it in 1928) and the French mineralogist ..., Fibrifold notation, geometric notation, and Coxeter notation: References * * * * * Symmetry Finite groups Discrete groups {{geometry-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coxeter Notation
In geometry, Coxeter notation (also Coxeter symbol) is a system of classifying symmetry groups, describing the angles between fundamental reflections of a Coxeter group in a bracketed notation expressing the structure of a Coxeter-Dynkin diagram, with modifiers to indicate certain subgroups. The notation is named after H. S. M. Coxeter, and has been more comprehensively defined by Norman Johnson. Reflectional groups For Coxeter groups, defined by pure reflections, there is a direct correspondence between the bracket notation and Coxeter-Dynkin diagram. The numbers in the bracket notation represent the mirror reflection orders in the branches of the Coxeter diagram. It uses the same simplification, suppressing 2s between orthogonal mirrors. The Coxeter notation is simplified with exponents to represent the number of branches in a row for linear diagram. So the ''A''''n'' group is represented by ''n''−1 to imply ''n'' nodes connected by ''n−1'' order-3 branches. Exam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Truncated Octahedra
In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces (8 regular hexagons and 6 squares), 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a 6-zonohedron. It is also the Goldberg polyhedron GIV(1,1), containing square and hexagonal faces. Like the cube, it can tessellate (or "pack") 3-dimensional space, as a permutohedron. The truncated octahedron was called the "mecon" by Buckminster Fuller. Its dual polyhedron is the tetrakis hexahedron. If the original truncated octahedron has unit edge length, its dual tetrakis hexahedron has edge lengths and . Construction A truncated octahedron is constructed from a regular octahedron with side length 3''a'' by the removal of six right square pyramids, one from each point. These pyramids have both base side length (''a'') and lateral sid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tristram Carfrae
Tristram George Allen Carfrae, FRSA, FREng, FTSE, RDI (born 1 April 1959) is a British-Australian structural engineer and designer. He is currently Deputy Chair of Arup and an Arup Fellow. Carfrae was awarded the Gold Medal of the Institution of Structural Engineers in 2014. He became the fourth Briton to be awarded the International Award of Merit in Structural Engineering by the International Association for Bridge and Structural Engineering in 2018. In 2018-19 he was Master of the Royal Designers for Industry. Working in both Australia and UK, Carfrae has contributed (code word) to the design of many projects with notable architects such as Richard Rogers, Renzo Piano, Philip Cox and Thomas Heatherwick, these include: Lloyd's of London, Stadio San Nicola, Aurora Place, City of Manchester Stadium, Beijing National Aquatics Center (the Water Cube), Helix Bridge, One One One Eagle Street, Singapore Sports Hub, Coal Drops Yard and he is currently helping to complete the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beijing National Aquatics Centre
The National Aquatics Centre (), and colloquially known as the Water Cube () and the Ice Cube (), is an aquatics center at the Olympic Green in Beijing, China. The facility was originally constructed to host the aquatics competitions at the 2008 Summer Olympics and Paralympics. During the Olympics — where it hosted diving, swimming and synchronized swimming events — 25 world records were broken in swimming. In July 2010, a renovation of the facility was completed, which included the addition of a public water park. With Beijing being awarded the 2022 Winter Olympics, the Water Cube became known as the Ice Cube as part of the Water Cube was renovated in 2019 to allow the hosting of curling events. Architecture In July 2003 the Water Cube design was chosen from 10 proposals in an international architectural competition for the aquatic center project. The Water Cube was specially designed and built by a consortium made up of PTW Architects (an Australian architecture fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
2008 Summer Olympics
The 2008 Summer Olympics (), officially the Games of the XXIX Olympiad () and also known as Beijing 2008 (), were an international multisport event held from 8 to 24 August 2008, in Beijing, China. A total of 10,942 athletes from 204 National Olympic Committees (NOCs) competed in 28 sports and 302 events, one event more than those scheduled for the 2004 Summer Olympics. This was the first time China had hosted the Olympic Games, and the third time the Summer Olympic Games had been held in East Asia, following the 1964 Olympics in Tokyo, Japan, and the 1988 Olympics in Seoul, South Korea. These were also the second Summer Olympic Games to be held in a communist state, the first being the 1980 Summer Olympics in the Soviet Union (with venues in Russia, Ukraine, Belarus, and Estonia). Beijing was awarded the 2008 Games over four competitors on 13 July 2001, having won a majority of votes from members of the International Olympic Committee (IOC) after two roun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Pursuit Of Perfect Packing
''The Pursuit of Perfect Packing'' is a book on packing problems in geometry. It was written by physicists Tomaso Aste and Denis Weaire, and published in 2000 by Institute of Physics Publishing ( doi:10.1887/0750306483, ) with a second edition published in 2008 by Taylor & Francis (). Topics The mathematical topics described in the book include sphere packing (including the Tammes problem, the Kepler conjecture, and higher-dimensional sphere packing), the Honeycomb conjecture and the Weaire–Phelan structure, Voronoi diagrams and Delaunay triangulations, Apollonian gaskets, random sequential adsorption, and the physical realizations of some of these structures by sand, soap bubbles, the seeds of plants, and columnar basalt. A broader theme involves the contrast between locally ordered and locally disordered structures, and the interplay between local and global considerations in optimal packings. As well, the book includes biographical sketches of some of the contribu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nature (journal)
''Nature'' is a British weekly scientific journal founded and based in London, England. As a multidisciplinary publication, ''Nature'' features peer-reviewed research from a variety of academic disciplines, mainly in science and technology. It has core editorial offices across the United States, continental Europe, and Asia under the international scientific publishing company Springer Nature. ''Nature'' was one of the world's most cited scientific journals by the Science Edition of the 2019 '' Journal Citation Reports'' (with an ascribed impact factor of 42.778), making it one of the world's most-read and most prestigious academic journals. , it claimed an online readership of about three million unique readers per month. Founded in autumn 1869, ''Nature'' was first circulated by Norman Lockyer and Alexander Macmillan as a public forum for scientific innovations. The mid-20th century facilitated an editorial expansion for the journal; ''Nature'' redoubled its efforts in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
New York Times
''The New York Times'' (''the Times'', ''NYT'', or the Gray Lady) is a daily newspaper based in New York City with a worldwide readership reported in 2020 to comprise a declining 840,000 paid print subscribers, and a growing 6 million paid digital subscribers. It also is a producer of popular podcasts such as '' The Daily''. Founded in 1851 by Henry Jarvis Raymond and George Jones, it was initially published by Raymond, Jones & Company. The ''Times'' has won 132 Pulitzer Prizes, the most of any newspaper, and has long been regarded as a national "newspaper of record". For print it is ranked 18th in the world by circulation and 3rd in the U.S. The paper is owned by the New York Times Company, which is publicly traded. It has been governed by the Sulzberger family since 1896, through a dual-class share structure after its shares became publicly traded. A. G. Sulzberger, the paper's publisher and the company's chairman, is the fifth generation of the family to head the p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete & Computational Geometry
'' Discrete & Computational Geometry'' is a peer-reviewed mathematics journal published quarterly by Springer. Founded in 1986 by Jacob E. Goodman and Richard M. Pollack, the journal publishes articles on discrete geometry and computational geometry. Abstracting and indexing The journal is indexed in: * ''Mathematical Reviews'' * ''Zentralblatt MATH'' * ''Science Citation Index The Science Citation Index Expanded – previously entitled Science Citation Index – is a citation index originally produced by the Institute for Scientific Information (ISI) and created by Eugene Garfield. It was officially launched in 1964 ...'' * '' Current Contents''/Engineering, Computing and Technology Notable articles The articles by Gil Kalai with a proof of a subexponential upper bound on the diameter of a polyhedron and by Samuel Ferguson on the Kepler conjecture, both published in Discrete & Computational geometry, earned their author the Fulkerson Prize. References Externa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |






.png)